|
Le
chiffre d'affaires du PMU vient de baisser de trois pur-sang.
Coluche |
Notez
que pur-sang ne prend pas de
"s" au pluriel.
Voir
Pensées & humour / Orthographe / Orthographe des nombres
|
Une
légion romaine de 3 000 fantassins. Dix pourcent ont une lance; parmi les
autres, seule la moitié est armée de deux lances. Les autres ne sont pas
armés. Combien faut-il confectionner de lances pour cette légion ? |
__________________________________________________________________________________________________
Un super truc de calcul mental !
Si
le calcul du pourcentage vous semble compliqué, inversez le calcul …

Voir Calcul
mental / Commutativité
/ Brève
275
_______________________________________________________________________________________________________
|
POURCENTAGE
Proportion
de quelque chose pour 100 unités. Règle de trois pour laquelle l'un des
dénominateurs est fixé à 100. |
||
|
En pratique |
|
|
|
|
||
![]()
|
Remarque |
|
|
Notations |
|
|
Abréviation |
|
|
Décimal |
4,5
% = 4,5 / 100 = 0,045 |
|
Fraction |
|
![]()
|
Exemple: 12%
de 345 = 345 x 12 / 100 = 41,4 Il est normal que le résultat soit plus
petit que le nombre de départ.
Exemple: 345
+ 12% = 345 ( 1 + 12/100) = 345 + 41,4 = 386,4
Fameuse règle de trois (ou égalité des
produits en croix). x = 12 x 100 / 73 = 16,4 %
73 représente un peu moins des ¾ de 100. Pour aller à 100, il faudrait diviser par 3
et multiplier par 4. Même chose pour la colonne du 12. |
|||||||||||||||||||
|
Piège |
une augmentation de 20% ou deux de 10% l'une après l'autre.
Explication: deux fois 10% correspond à:
1,1 x 1,1 = 1,21 qui donne 21% soit plus que 20%. Si la deuxième
augmentation est différée, la réponse n'est pas immédiate car cette personne
aura un revenu de 22 keuros et non pas 24 pendant un certain temps.
une augmentation de 20% immédiate ou 10% maintenant et 10 % l'an prochain? Calcul:
une augmentation de 50% immédiate ou 10% maintenant et 25 % l'an prochain? Calcul:
La
première version est souvent citée pour dénoncer un défaut de raisonnement
avec les pourcentages et, c'est très bien. Cependant
dans la réalité, les augmentations sont différées dans le temps. Dans
ce cas, et aussi pour diverses raisons de conjoncture, il vaut souvent mieux
tenir la grosse augmentation dès que possible! |
![]()
|
|
Sommes-nous
tous égaux face aux pourcentages? Dessin de Tiounine (Russe) |
Voir Pensées & humour
EXEMPLES
|
|
|
|
Le cours boursier de cette société est juste à 100. Il
subit une croissance de 5% pendant 5 ans puis une baisse de 5% pendant 5 ans.
Quel sera son cour au bout des 10 ans? En hausse ou en baisse? F = 100 x 1,05 x 1,05 x 1,05 x 1,05 x 105 x 0,95 x
0,95 x 0,95 x 095 x 0,95 = 98,76 On peut
l'écrire: F = 100 x 1,055 x 0,955
Le graphique montre les effets d'une alternance de1%
(rouge), 5% (vert) et 10% (violet). |
|
|
|
|||||||||||||||
|
N
= B – B/10 = 9B / 10 ·
Selon que l'on connaît B ou N:
Illustration
·
Attention aux pourcentages, dans un sens ou dans
l'autre. |
|||||||||||||||
|
|
|||
|
Prix TTC 210 euros Tva 20% Prix HT? |
PTTC
= PHT + 0,2 PHT PHT
= PTTC / 1,2 = 210 / 1,2 = 175 € |
Il ne pas retrancher 20% à 210, mais bien reprendre la formulation
indiquée. La TVA s'applique au prix hors taxes, comme son nom l'indique. |
|
|
Doubler un capital (C). Les intérêts (I) sont égaux au capital. |
|
C'est posséder 200% du capital initial. C'est avoir gagné 100% en plus du capital. |
|
|
L'action chute de 10% et augmente de x% pour retrouver sa valeur
nominale. Valeur de x? |
|
Une action d e 100 euros passe à 90 (-10%). Pour remonter de 90 à 100 euros, elle doit gagner 10 par rapport à sa
valeur actuelle 90, soit 10/90 = 11,11…%. |
|
|
Votre placement vous rapporte 9% L'inflation est de 5% Quel est le rapport réel |
|
Ce n'est pas la différence 9 – 5 = 4%. Le calcul donne un peu moins, car l'inflation s'applique à la somme
acquise, soit 3,55% |
|
|
Placement de 1000 euros à 5% sur 10 ans. Votre gain? |
…
|
En laissant les intérêts sur le compte, la somme finale s'élève à 1
639 euros. Alors qu'en touchant les intérêts à la fin de chaque année, ce serait
seulement 1 500 euros. |
|
D'après un article publié par Le Revenu
|
|
||
|
Problème
|
Un drap rectangulaire de 300
cm x 200 cm. Ses dimensions se réduisent
de 3% suite au premier lavage. Quel est le pourcentage de
réduction de l'aire du drap. |
|
|
· Les dimensions de l'étoffe diminuent de 3 %. |
· Les dimensions sont bien la longueur et la largueur. · Chacune de ces dimensions rétrécit de 3%. |
|
|
Solutions |
|
|
|
1 ) Solution FAUSSES |
·
L'aire rétrécit comme le
produit des rétrécissements de la longueur et de la largueur. R = 3% x 3% = 0,03 x 0,03 =
0,0009 ou 3 10-2 x 3 x 10-2 =
9 x 10-4. Solution fausse avec
solution très éloignée du bon résultat >>> · Facile, comme la longueur et la larguer rétrécissent, ça fait deux
fois 3%, soit 6%. Ce raisonnement est totalement faux et pourtant, il nous
rapproche de la bonne réponse >>> |
|
|
2) La solution "laborieuse" |
Elle nécessite un calcul
complet. Les pourcentages sont
toujours traîtres! Alors, cette méthode permet
de se rassurer. |
|
|
· Longueur initiale: L = 320 cm |
L' = L – L x 0,03 = 300 – 300 x 0,03 = 291 cm |
|
|
· Larguer initiale: l = 230 cm |
l' = l – l x 0,03 = 200 – 200 x 0.03 = 194 cm |
|
|
· Aire de l'étoffe |
A = L x l
= 300 x 200 = 60 000 cm² A' = L' x l' = 291 x 194 = 56 454 cm² |
|
|
· Écart |
E = 60 000 – 56 454 = 3 546
cm² |
|
|
· Rapport |
|
|
|
3) La solution plus directe |
|
|
|
· On conserve les valeurs des pourcentages le long des calculs. · Ce qui évite le calcul numérique des aires. |
|
|
|
· Pour quelqu'un d'entraîné la réponse serait directement: |
R = 1 – 0,97² = 0, 0591= 5,91% |
|
|
Commentaires |
||
|
·
La solution
fausse 1 s'explique avec un dessin montrant les pourcentages. · Seule la partie bleue reste après rétrécissement. Elle correspond à
97% x 97%; alors que le petit rectangle en bas correspond à 3% x 3% ( les
pourcentages étant appliqués aux dimensions de l'étoffe). Ce qui explique la
solution et également la solution fausse. |
|
|
|
·
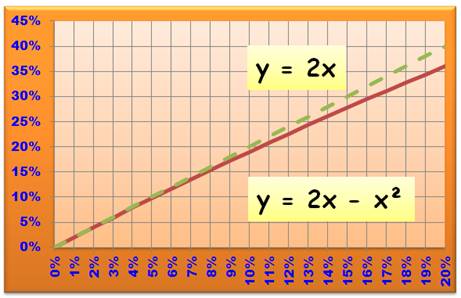
La solution fausse n°2
montre que le double de 3% est presque la bonne réponse: 6% est proche de 5,91%.
Est-ce un hasard? Non car, si x est le taux de rétrécissement, alors: R = 1 – ( 1 – x)² = 1 – 1 + 2x – x² = 2x – x². Ce nombre est effectivement
proche de 2x à x² près, un petit nombre si x est petit. |
|
|
|
3000 fantassins. 10% avec une lance et 50% des autres avec 2
lances. Cette moitié ayant deux lances, c'est comme si tous avaient
une lance et comme les autres 10% en ont une; alors, il faut fabriquer 3000
lances. Calcul ·
(10% de 3000) x 1 = 300 lances. ·
(50% de (3000 – 300) ) x 2 = 0,5 x
2700x 2 = 2700 lances. ·
Total:
300 + 2700 = 3000 lances. |
Calcul amusant des pourcentages

|
J'ai une façon secrète pour trouver
21% de 80. "J'adore les secrets." |
10% ça fait 8 et 1% ça fait 0,8. |
Alors 21% ça fait 8 + 8 + 0,8 = 16,8. "Sort d'ici !" |
Source image: Big
Ideas Learning – Cartoons
|
Anglais |
POURCENTAGE ·
An amount, number
or rate given as fraction of one hundred. We have expressed all
the figures as percentages. ·
Per cent : a fraction of one hundred. Ne pas prononcer "père-sans" à la française,
mais quelque chose comme "peu-si-ntt" avec l'accent à le fin. |
|
· Règle de trois pour exemples simples |
|
|
Voisins |
· Échelle · Intérêts |
|
En savoir plus |
· Brève
275 – Pourcentage (truc de calcul) · Calcul mental –
Index · Calcul mental
– La méthode Fermi · Énigmes sur la dilution ou la
déshydratation · Fractions – Glossaire · Pente · Pente - débutant · Pourcentage
de nombres avec 3 · Pourcentage
de nombres premiers |
|
Cette page |
http://villemin.gerard.free.fr/Referenc/Vocabula/GlosP/Pourcent.htm |
![]()