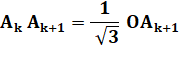|
||||||||||||||||||||||||||||||||||||||||
![]()
Baccalauréat S 2018
|
Une pétition très suivie a été émise protestant contre la
difficulté du quatrième exercice, jugé infaisable, et contre le troisième considéré
comme hors-programme. Cet exercice "n°4 – non spécialité" a semblé trop
calculatoire et sans possibilité de se rassurer en cours de route. |
Baccalauréat S Session 2018 Mathématiques "Normal" Exercice n°4 |
Voir Enseignement
– Index
|
|
|||
|
Le plan
complexe est muni d’un repère orthonormé direct :
On pose z0
= 8 et pour tout entier naturel
n :
On note An
le point du plan d’affixe xn. |
Rappels Repère orthonormé >>> Nombres complexes
en terminale >>> Affixe :
coordonnées d'un point du plan donnée par sa notation complexe : z
= a + ib. Récurrence : la
valeur de la variable à l’itération n+1 est déduite de sa valeur à
l’itération précédente n >>> |
||
|
1a)
Vérifiez que
|
Ce qui est
demandé, en fait : passage de la présentation algébrique à la présentation
polaire. Il faut connaitre le module (longueur) et
l'argument (angle) Alors : a – i b devient |
||
|
Partie réelle
& Partie
imaginaire |
|
||
|
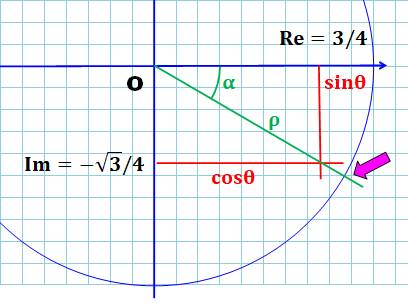
Représentation À faire à main levée et sans se soucier de l’échelle Si possible tout de même sur u papier quadrillé en respectant l’ordre
de grandeur. L’angle est très proche de – 30° car la droite verte coupe le cercle
trigonométrique pour y = - 0,5 (grosse flèche mauve). |
|
||
|
Module |
|
||
|
Le calcul de
l’argument passe par le calcul du sinus et du cosinus de l’angle |
|
||
|
Forme
exponentielle de ce nombre que l’on baptise z |
|
||
|
1b) En
déduire l’écriture de chacun des nombres complexes z1, z2,
z3 sous forme exponentielle et vérifiez que z3 est un imaginaire
pur dont on précisera la partie imaginaire. |
Un produit ! La forme exponentielle s’y
prête bien : Produit des modules et addition des arguments |
|
|
Calcul des zi |
|
|
|
L’argument de z3
est un angle en 90°, c’est un complexe
imaginaire pur |
|
|
|
1c)
Représenter graphiquement les points A0, A1, A2,
A3 ; on prendra pour unité le centimètre. |
|
|
A0 correspond à z = 8, un réel qui se
trouve sur l’axe des x, abscisse 8. A1 est le rayon d’angle – 30° et avec
une longueur de 6,92. A2 est le rayon d’angle – 60° et avec
une longueur de 6. A3 est le rayon d’angle – 90° et avec
une longueur de 5,2. Ce qui confirme son statut d’imaginaire pur négatif. |
|
2a)
Démontrer par récurrence que, pour tout entier n,
|
La démonstration
par récurrence consiste à vérifier que cette relation est vraie au début
et que, étant supposée vraie pour n elle est aussi vraie pour n + 1 |
|
|
Vraie pour z1 |
|
|
|
Valeur pour zn+1 On se souvient que : an+1 = an . a e(n+1)k = en.k . ek |
Ce qui est bien notre formule de récurrence |
|
|
2b) Pour
tout entier n, on pose
Déterminer
la nature et la limite de (un). |
L’idée consiste à recalculer la formule de
récurrence dans ce cas. On rappelle que /z/ est le module, soit le
coefficient devant l’exponentielle. |
|
Récurrence en
reprenant la formule initiale de l’énoncé |
|
|
On a calculé le module
du premier terme |
|
|
Reprenons |
|
|
C’est une suite
géométrique de raison rac(3)/2, inférieure à 1 |
|
|
Comportement de
la suite (chaque nouveau terme diminue) |
|
|
3a)
Démontrer que, pour tout entier naturel k,
En
déduire que, pour tout entier naturel k, on a l’égalité
|
Simple calcul avec des nombres complexes, sans
oublier l’emploi du conjugué. Le numérateur est une soustraction de nombres
complexes. La somme donnerait la longueur de diagonale issue de
l’origine ; la soustraction donne la longueur de l’autre diagonale, le
segment qui joint les deux points représentés.
|
|
Calcul du
numérateur, toujours avec la formule initiale |
|
|
En divisant par
le dénominateur |
|
|
Multiplication
du dénominateur par le conjugué pour sortir la racine |
|
|
Transformation
de la relation en termes de longueurs (cf. remarque liminaire) |
|
|
3b) Pour tout
entier naturel n, on appelle ln la longueur de la ligne brisée
reliant dans cet ordre les points A0, A1, A2,
A3 … An-1, An. On a
ainsi : ln = A0A1 + A1A2
+ … + An-1An. Démontrer
que la suite (ln) est convergente et calculer la limite. |
La ligne brisée
invoquée est constituée des segments qui relient tous les points les uns
après les autres. La longueur demandée est la somme des longueurs
calculées précédemment pour chaque segment. |
|
Somme des
longueurs Avec OA =
/z/ = u, calculé précédemment |
|
|
Or u est une
suite géométrique Formule de
calcul de la somme :
|
|
|
Pour n tendant
vers l’infini la puissance n de (rac(3) / 2 = 0,866 < 1) tend vers 0. Résulta
final obtenu en multipliant par le
conjugué. |
|
|
Suite |
Voir haut
de page |
|
Voir |
|
|
Cette page |