|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
![]()
|
L'arithmétique
sert à compter et à mesurer des longueurs. L'algèbre
est un outil facilitant la
résolution des équations. La géométrie étudie la propriété des objets
dans l'espace. L'analyse (dérivées et intégrales) s'intéresse aux mouvements La trigonométrie est un procédé de calcul relatif aux angles. |
|
La pire crainte du cosinus?
Attraper une sinusite. |
Voir Pensées & humour
|
TRIGONOMÉTRIE Spécial DÉBUTANTS Je n'y comprends rien! C'est du chinois! Pourquoi diable, avoir inventé quelque chose d'aussi
barbare? Le cercle trigonométrique
quèsaco? Le sinus
et le cosinus quèsaco ? |
En bref, pourquoi la trigo?
|
Les
Anciens utilisaient la formule du triangle
de Pythagore pour résoudre des problèmes sur les triangles. Cela
est devenu bien vite insuffisant. On en est venu à faire des tables qui
associaient un angle du triangle
rectangle à la longueur de ses côtés. Ces mesures ont été baptisées sinus pour le côté opposé, cosinus pour le côté
à côté et tangente
pour le rapport entre les deux. Pour
s'y retrouver et disposer d'une référence commune, les mathématiciens ont
normalisé le "terrain de jeu" en disant que
tous les triangles rectangles considérés seront posés sur un cercle de rayon unité. Le point M, qui se déplace sur la circonférence du cercle, devient le centre
d'intérêt. La
trigonométrie ce n'est pas plus que cela, au
départ. L'outil c'est révélé si puissant que cette branche des mathématiques
s'est considérablement développée au service de nombreux domaines, comme l'astronomie, le calcul des images,
l'électronique … |
|
![]()
|
|
||
|
Triangle rectangle isocèle
Constat
Plus grand plus petit
Jusqu'ici,
rien de compliqué, de la géométrie élémentaire |
|
|
|
|
||
|
Triangle rectangle
|
Pour Pour Pour |
|
|
C'est
ici qu'intervient la trigonométrie Qui n'est pas beaucoup
plus qu'une bibliothèque (une base de
données) des valeurs de a et b selon les angles |
||
|
|
||
|
Triangle quelconque
|
|
|
|
En résumé Le triangle rectangle isocèle est un
cas particulier. Le triangle quelconque se ramène au
triangle rectangle. Le triangle rectangle se calcule à
l'aide de la trigonométrie. Dans le triangle rectangle, la trigonométrie donne les longueurs des côtes en
fonction d'un angle. On rappelle que la trigonométrie s'applique
exclusivement aux triangles
rectangles. Mais, tout triangle peut être
découpé en deux triangles rectangles ayant la hauteur du premier comme côté commun. |
|
|
||
|
Explication détaillée pour
bien comprendre la notion de cercle trigonométrique |
||
|
|
Le point M est toujours sur le cercle. |
|
|
-1 et +1 |
Les coordonnées du point M, x et y, prennent des
valeurs comprises entre -1 et +1. |
|
|
La notation à
droite correspond aux angles orientés
|
En trigonométrie les coordonnées du point
s'appellent cosinus et sinus. Ce sont des valeurs qui caractérisent aussi
l'angle t. Elles prennent des valeurs exclusivement entre -1 et +1. Une valeur de cosinus caractérise deux points sur
le cercle: M et M'. Une valeur de sinus caractérise deux points sur
le cercle: M et M". |
|
|
|
En parcourant le périmètre (P = 2 |
|
|
Voir Ces valeurs et
d'autres sur le cercle
De sorte que: la valeur de
l'angle t en radians est aussi la valeur de la longueur de l'arc de cercle
intercepté par l'angle t. Par exemple: l'angle AOC vaut 180° = Pi radians = 3,14… radians; La longueur de
l'arc ABC est égale à 3,14 unités, l'unité de longueur étant celle de R le
rayon du cercle. |
||
|
Sur
le cercle trigonométrique, un point M
définit un angle t dont abscisse (x = cosinus)
et ordonnée (y = sinus) caractérisent cet angle. Le
radian est une mesure d'angle en même
temps qu'une mesure de longueur sur le cercle trigonométrique (R = 1 unité de
longueur). |
Voir Trigonométrie: définitions
et formulaire
Graphes des fonctions sin x et cos x (périodique de période
2 Pi)

![]()
|
|
||
|
|
|
|
|
|
||
|
Question
Réponse
Aire du pré vert en bas: Ac=
c² = cos² (t). Or dans un triangle
rectangle (Pythagore):
|
|
|
Voir Énigmes de chèvres dans un pré
Retenons de ces énigmes
|
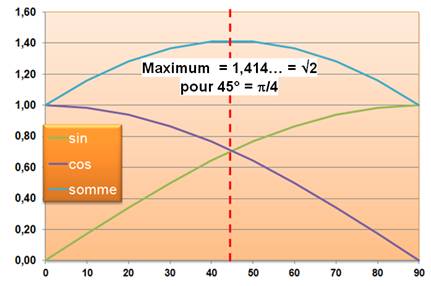
sin(t) + cos(t)
= { de 1 à 1,4142… = sin²(t) + cos²(t)
= 1 |
![]()
|
Suite en |
|
|
Voir |
|
|
Site |
|
|
Cette
page |
![]()