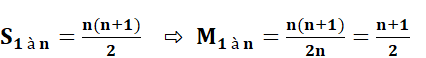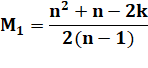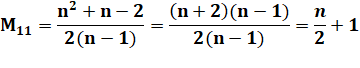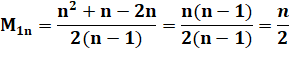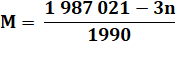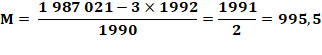NOMBRES - Curiosités, théorie et usages Accueil DicoNombre Rubriques Nouveautés Édition du: 26/01/2020 Orientation générale  DicoMot Math Atlas Actualités M'écrire Barre de recherche DicoCulture Index alphabétique Références Brèves de Maths
	COMPTER
Débutants Général	MOYENNES				Glossaire Général
INDEX Compter Dénombrer Calcul	Débutants	Introduction	Comparaison	Confiance
		Somme entiers	Carré magique
		Sommaire de cette page >>> Approche – Nombres de 1 à 10 >>> Solution de l'énigme 1 >>> Cas de M1 = …,75 >>> Solution de l'énigme 2

Énigme de l'entier manquant

Moyenne connue

Deux types d'énigmes avec la somme des entiers de 1 à n:

Il faut retrouver l'entier k retiré: soit en connaissant la nouvelle somme S >>> soit en connaissant la nouvelle moyenne M >>> (cette page)

Moyenne de la somme des entiers

La moyenne des nombres de 1 à n est un nombre entier pour n impair. >>>

Énigmes

1) Parmi les nombres consécutifs de 1 à n, on retire un nombre et on calcule la moyenne: 40,75. Quel est le nombre retiré?

2) Parmi les nombres de 1 à 1993, on retire trois entiers consécutifs est la moyenne est un nombre entier. Quels sont ces trois nombres ?

Solution 1 / Solution 2

Approche – Nombres de 1 à 10
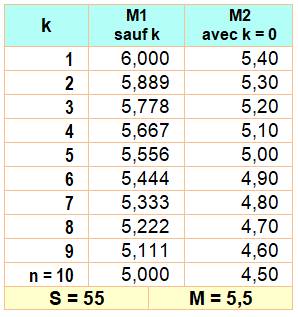
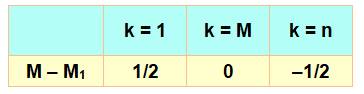
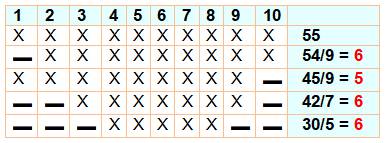
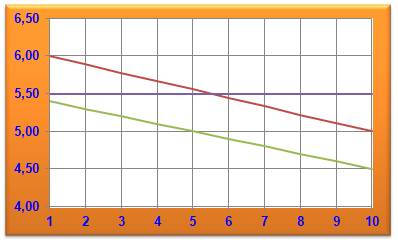
La somme des nombres de 1 à 10 vaut 55 et la moyenne est 55 / 10 = 5,5. Comment évolue la moyenne quand on ampute la suite d'un nombre k ? si k est retiré, on retire sa valeur de la somme et surtout on divise par 9 pour obtenir la nouvelle moyenne M1; ou si on met k à 0, on retire k à la somme et on divise par 10 pour obtenir la nouvelle moyenne M2. Le graphique aide à comparer les moyennes: Moyenne M en violet, droite horizontale; Moyenne M1 en rouge, oblique qui coupe la précédente au point (k = 5,5 et M1 = 5,5); et Moyenne M2 en vert, oblique en dessous de la première. Conclusion Dans le cas où le nombre k est supprimé, la nouvelle moyenne est située de part et d'autre de la moyenne originelle; à plus ou moins ½ de 5,5.
Justification Somme des nombres de 1 à n à laquelle on retire k:
Moyenne pour ces n – 1 nombres:
Valeurs extrêmes pour k = 1 Dans tous les cas, la moyenne maximale est égale à la moitié de n plus 1.
Valeurs extrêmes pour k = 1 Dans tous les cas, la moyenne minimale est égale à la moitié de n.
Conclusions	La moyenne de la somme des entiers, amputée d'un nombre k, varie entre n/2 et n/2 + 1. L'amplitude de variation est limitée à une unité. Plus précisémént pour la différence entre ces moyennes:
Application Rappel M = (1 + n) / 2 n = 2M – 1	Si la moyenne est égale à 40,75, (comme dans l'énigme),

Solution de l'énigme n°1
Énigme Parmi les nombres consécutifs de 1 à n, on retire un nombre et on calcule la moyenne: 40,75. Quel est le nombre retiré ?	Commentaires On se trouve bien dans le cas où un nombre k est retiré et la nouvelle moyenne se calcule avec un élément en moins. La familiarisation vue ci-dessus nous montre que si la moyenne devient 40,75, c'est que la moyenne originelle M est un entier autour de cette valeur.
Résolution en tableau Vérification: S1à81 = 81x82/2 = 3 321; S1 = 3 321 – 61 = 3 260 et 3260 / 80 = 40,75 Note: 40,75 raté de peu, car: Avec n = 80 et en retirant le nombre 20, la moyenne devient: 40,7595… Avec n = 80 et en retirant le nombre 21, la moyenne devient: 40,7468… Note avec 40,5 de moyenne, deux solutions: n = 79 et on retire 1 ou n = 81 et on retire 81.

Cas de M1 = …,75
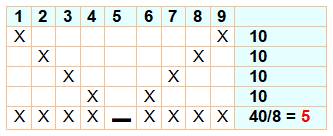
On examine les sommes et les moyenne M1 après avoir éliminé un nombre. Avec n = 5, somme 15, en ôtant le 1 M1 = 3,5; en ôtant le 4, M1 = 2,75, en jaune car c'est ce que l'on cherche. Avec n = 6 ou 7 ou 8, aucune possibilité d'obtenir une moyenne en …,75 Chose que l'on retrouve avec n = 9, 13 puis, en poursuivant, avec 17, 21 … 4n + 1.
Conclusions	Seules les valeurs de n en 4k + 1 donnent une moyenne en …,75 lorsqu'on retire l'un des nombres.
Application à notre énigme	Dans le cas de l'énigme, la quantité de nombres doit être en 4k + 1 et proche de 80, disons 81. La somme de 1 à 81 est égale à ½ (80 x 81) = 3 321. Or la somme des nombres sans x est 40,75 x 80 = 3 260. C'est que x = 3 321 – 3 260 = 61.

Solution de l'énigme n°2
Énigme Parmi les nombres de 1 à 1993, on retire trois entiers consécutifs, et la moyenne est un nombre entier. Quels sont ces trois nombres ?	La somme normale de ces entiers est égale à ½ 1993 x 1994 = 1 987 021 Moyenne: 1 987 021 / 1993 = 997 Voir Solution simple La somme des trois nombres retirés vaut: (n – 1) + n + (n + 1) = 3 n
Solution La nouvelle moyenne pour les 1990 nombres restants est un entier M tel que:
Examen des extrêmes avec n = 2 ou 1992 qui donne l'amplitude des recherches. Effectivement: n = (996, 997 ou 998)
Test de ces valeurs Les trois nombres sont donc: 996, 997 et 998	M996 = 997,0015… M997 = 997 M998 = 996,9984…
Généralisation On retire trois nombres consécutifs parmi les nombres de 1 à A. La moyenne des ces nombres est entière pour n = (a + 1) / 2.	Exemples a = 1999 => n = M = 1000 a = 2017 => n = M = 1009

Extraordinaire ? Non ! Avec a = 9, en retirant le 5 central, la moyenne des nombres restants est 5. En retirant une paire symétrique, la moyenne reste égale à 5. Même en retirant plusieurs paires. Par contre, retirer un nombre quelconque autre que le central produit une moyenne fractionnaire, non réductible à un entier.
Cas des nombre pairs Avec a = 10, en retirant le premier ou le dernier la moyenne est un nombre entier. En retirant, une extrémité et les paires symétriques par rapport aux nombres restants, la moyenne reste un nombre entier.
Bilan	La moyenne des nombre de 1 à A, A étant impair, reste un nombre entier lorsqu'on retire le nombre central et autant de paires symétriques que l'on veut. La moyenne des nombre de 1 à A, A étant pair, reste un nombre entier lorsqu'on retire un des nombres extrêmes et autant de paires symétriques sur ce qui reste.

Retour	Moyenne – Introduction
Suite	Comparaison entre les moyennes Énigme de l'entier manquant – Somme connue Somme des nombres de 1 à n Énigmes – Index Voir haut de page
Voir	Dénombrement Isopérimètre Moyenne et médiane Opérations
Cette page	http://villemin.gerard.free.fr/aMaths/Moyenne/SomEnt.htm