|
|||||||||||||||||||||||||||||||||||||||||||||
![]()
|
VECTEURS Introduction pour débutants Un vecteur est un outil
mathématique. "Vecteur" est un mot pour désigner une flèche indiquant une direction dans l'espace. On
connait les nombres
qui mesurent les segments de droites
qui sillonnent l'espace. Les vecteurs associent les deux en spécifiant une
direction et une longueur. En physique, la première application
consiste à représenter par un vecteur une force
appliquée dans une direction et selon
une certaine intensité. Cette page est dédiée à ceux
qui découvrent les vecteurs pour la première fois et ne comprennent pas tout
de suite ce qu'ils sont et à quoi ils servent. Ce n'est pas un cours, mais une
explication destinée à créer un déclic de compréhension. |
Anglais: Vector / Euclidean vector
Image qui démontre la
"force du vecteur"

Voir Pensées & humour
|
|
|||
|
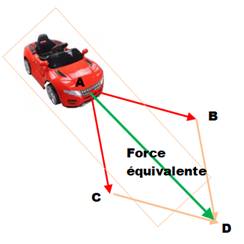
Exemple 1 Cette
flèche qui montre le déplacement de la voiture de sport est un VECTEUR. C'est
aussi simple! |
Le vecteur est le nom mathématique
pour une flèche. |
||
|
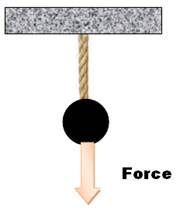
Exemple 2 Un boulet qui pèse
1 kg est suspendu au plafond,
tenu par une corde. Le boulet ne tombe pas, il est accroché au plafond. Mais,
il "tire" sur la corde. On peut imaginer
qu'une flèche représente la force du
boulet qui tire vers le bas. On appelle cette flèche symbolique: un vecteur. (Du latin
vector, dérivé de veho, transporter, comme dans l'expression: le moustique
est vecteur de maladies) |
|
||
|
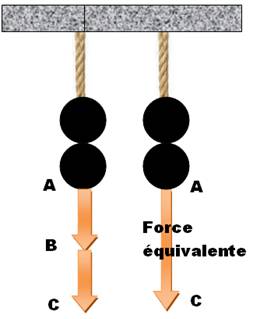
Première expérience avec les
vecteurs Avec un second
poids, on imagine bien que la force sera doublée (2 kg de force). Voir Unités de force On vient tout
simplement d'ajouter deux vecteurs! Recette: cela revient à effacer le B répété deux fois au centre de la somme. |
|
||
|
Le vecteur est un objet mathématique qui possède trois
caractéristiques: grandeur, direction et sens.
La grandeur du vecteur s'appelle la norme. Définition: soit A et B deux
points distincts, le vecteur
Pourquoi sens et direction ?
On dit bien je me dirige dans la direction de l'est. Donc
"direction" devrait suffire. Oui, mais on dit aussi une droite de
direction verticale sans préciser si elle va vers le bas ou vers le haut. Bah! Je dis bien: je suis sur l'autoroute en direction
de Nice et alors tout est dit! Certes.
Mais, pour le garagiste qui viendra te chercher mieux vaut lui préciser la
voie sur laquelle tu te trouves; je
suis sur l'autoroute A8 (Aix-Nice), dans le sens de Nice vers Aix. Bref, en maths, on aime la précision, alors on donne la
direction générale (il y en a une
infinité) et le sens (il y en a deux) sur cette direction. |
Voir DicoMot Maths Vecteur
|
|
||
|
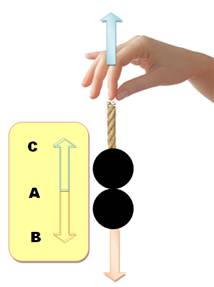
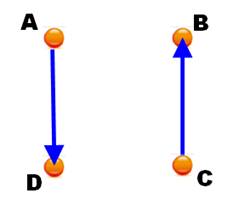
Maintenant prenons
la corde avec la main et maintenons l'équilibre. Il faudra tirer avec une
force de 1 kg. On symbolise cela avec la flèche bleue dans l'autre sens. On vient de soustraire
deux forces. L'une a un effet contraire à l'autre. Les vecteurs sont alignés,
alors en terme de forces: En vecteurs, cela
donne AB + AC = 0, le vecteur nul. Recette: on retrouve encore le B central qui s'efface.
Ici, le vecteur résultat est AA, c’est-à-dire un point. D'où cette notion de
vecteur nul. |
|
|
|
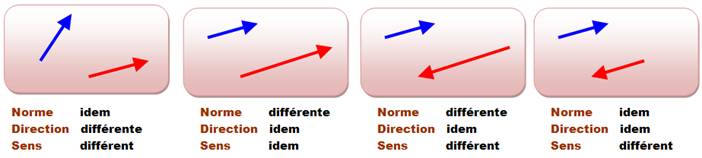
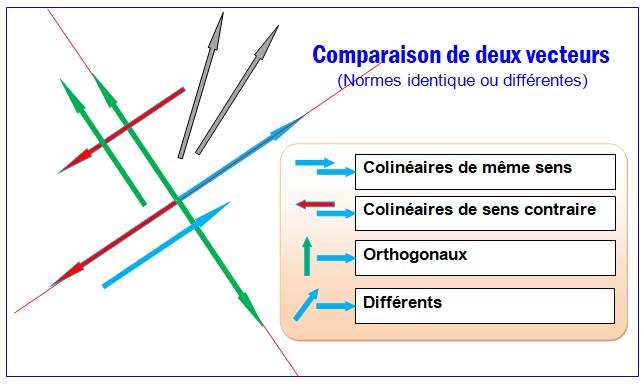
Variété de situations
|
|
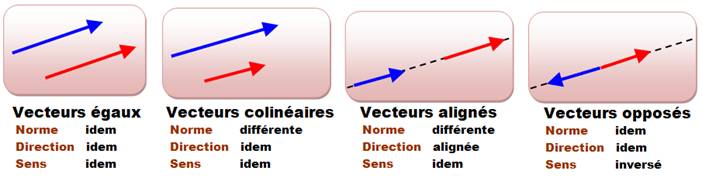
Noms de couples de vecteurs
|
|
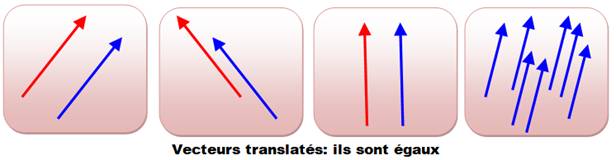
Égalité Deux vecteurs non nuls sont égaux si
et seulement si ils ont même direction, même sens et
même longueur.
|
Voir Translation
(traduisez: glissement sans rotation)
Attention: SENS
|
Le SENS d'un vecteur a une définition précise: il
indique le point départ d'un vecteur et son point d'arrivée. Le SENS pour deux vecteurs est une indication du
langage courant: il indique que les vecteurs pointent dans la même direction
ou dans la direction opposée ou dans des directions différentes. |
Merci à Alain OUDJOUDI
pour ses remarques
|
|
||
|
Après les vecteurs
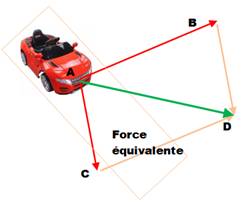
alignés, passons aux vecteurs de direction quelconque. Si on tire la
petite voiture avec une ficelle, elle va aller tout droit; dans le sens où on
tire. Facile! Mais que se
passe-t-il si deux enfants de même force tirent chacun sur une ficelle,
chacun de son côté ? D'abord, la force ne sera pas égale
à 2, car on "perd" un peu de force à vouloir tirer sur les côtés.
Ensuite, si les forces sont les mêmes, la voiture va avancer sur le trajet central, droit devant elle,
comme avec une seule ficelle. |
|
|
|
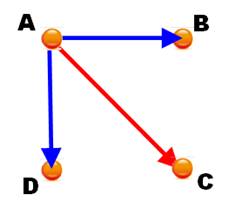
On a montré que
tout se passe comme si la force équivalente était dessinée par la diagonale du
parallélogramme dessinée à partir des deux vecteurs à ajouter. En vecteurs cela donne:
AB + AC = AD. Recette: Comme AB
et CD sont "équivalents", pour dessiner le parallélogramme, il suffit
de mettre le vecteur AC au bout du vecteur AB. |
|
|
|
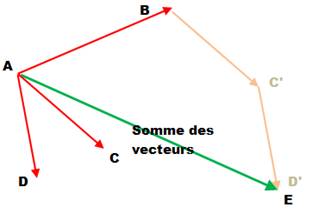
Pour faire une somme de vecteurs: je mets
les vecteurs les uns au bout des autres. Pratique non? Sur ce dessin, on
montre comment appliquer cela pour trois vecteurs. On met les vecteurs
équivalents, bout à bout: AB + AC +
AD = AB + BC'
+ C'D' = AD' = AE On voit que les points intermédiaires comme C'
s'éliminent. Exemple: la somme des vecteurs AB + BC + CD + DE +…YZ est égale à AZ. |
|
|
|
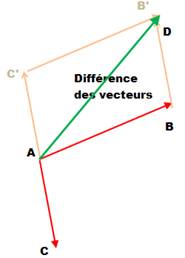
Pour faire la soustraction de AB et AC, on se ramène à une
addition en dessinant le vecteur AC' opposé de AC (le même, mais dans l'autre
sens) et on effectue la somme: |
|
|
|
La règle du parallélogramme: pour les additionner, on
met les vecteurs bout à bout. La relation de Chasles: les point intermédiaires (qui
se répètent) d'effacent :
Vecteurs
opposés: si AB + BA = 0, les vecteurs AB et BA
sont opposés et AB = – BA. Ils sont
alignés. Pour
avoir un sens, formellement, il faut mettre un chapeau
aux vecteurs:
|
|
|
|
|
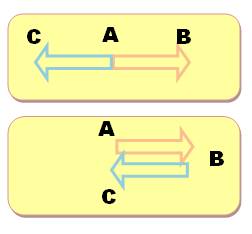
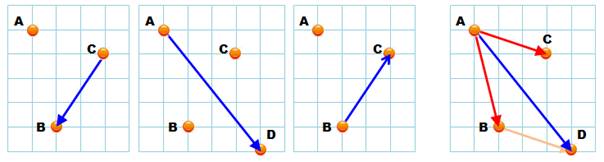
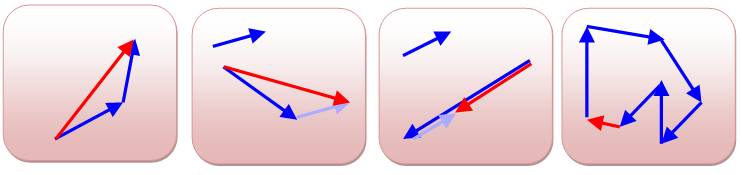
Parmi les trois
figures, dire quel dessin représente:
Pour cela, on trace
le parallélogramme (figure de droite) ou on met bout à bout les deux
vecteurs. La somme est représentée par le vecteur AD.
C'est la figure du
centre qui représente la somme demandée. |
|
Somme Vecteurs bleus = Vecteur rouge
|
|
||
|
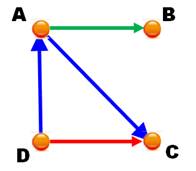
Si ABCD est un
carré, dire si les affirmations suivantes sont vraies ou fausses. |
||
|
AB + AD = AC |
AD = CB |
|
|
|
|
|
|
On
dessine mentalement le parallélogramme (ici, un carré) et on vérifie
qu'effectivement l'égalité est correcte.
(Note:
sans le chapeau ^, l'égalité proposée n'a pas de sens). |
S'agissant
d'un carré, les côtés AD et CB sont bien de même mesure. L'égalité sans le
signe vecteur est correcte. Par
contre, avec les vecteurs:
|
|
|
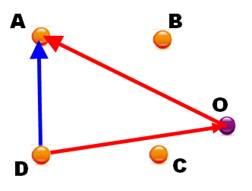
DO + OA = DA |
|
|
|
|
|
Le
point O est quelconque. Cette
égalité n'a de sens qu'avec la mention vecteur:
Le
tracé du parallémigramme montre que cette somme est exacte. D'ailleurs la recette de l'effacement
du point central montre immédiatement que c'es bon (le O disparait) Plus mathématiquement: on applique la
relation de Chasles qui donne immédiatement la solution. |
Le
dessin du parallélogramme montre que la somme vaut Plus mathématiquement:
Communtativité (on peut
inverser)
Relations de Chasles
Équivalence des vecteurs
|
|
|
||
|
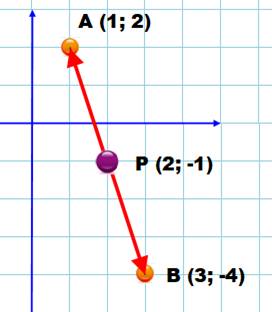
Problème Deux
points A (1; 2) et B (3, -4) Coordonnées
du point P tel que Solution Si
le vecteur-somme est nul, les vecteurs sont alignées et de sens opposés.
Le
point P est au milieu du segment AB. Soit en abscisse: (1 + 3)
/ 2 = 2 Et en ordonnées: (2 – 4 )
/ 2 = – 1 Les
coordonnée du point P: P (2; -1) |
Vérification graphique
|
|
|
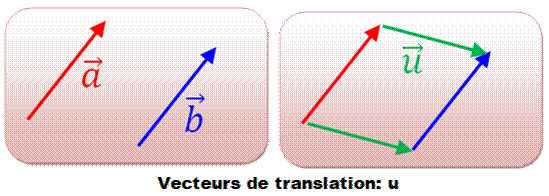
Retour au premier exemple montrant le déplacement
d'une voiture de sport. Ici, on définit la translation par un vecteur (u) qui
spécifie direction, sens et grandeur
du déplacement. Ce déplacement s'appelle une translation.
Le vecteur b est l'image du vecteur a par la
translation u. Les vecteurs a et b sont égaux. |
![]()
|
Retour |
|
|
Suite |
|
|
Voir |
|
|
Sites |
|
|
Cette page |
http://villemin.gerard.free.fr/aMaths/Outils/Matrice/Vecteur.htm |
![]()