NOMBRES - Curiosités, théorie et usages Accueil / Dictionnaire / Rubriques / Index / Atlas / Références / Nouveautés ORIENTATION GÉNÉRALE  - M'écrire - Édition du: 01/02/2012
Débutants Général	SCIENCES Physique				Glossaire Général
	LEVIER – Les bases
	Levier	Treuil	Plan incliné	Support
	Forces	Poussée
Sommaire de cette page >>> Approche >>> Somme des forces >>> Cas de la barre inclinée >>> Cas du plan incliné

---

Approche: jeux de cordes
À deux Au jeu de la corde, si chacun tire avec la même force F, la corde ne bouge pas. On note simplement que: l'une des forces est dans un sens et l'autre est dans l'autre sens. Les forces ont même intensité, mais elles s'opposent.
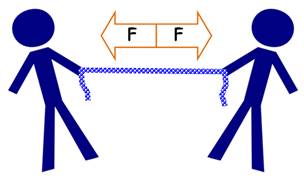
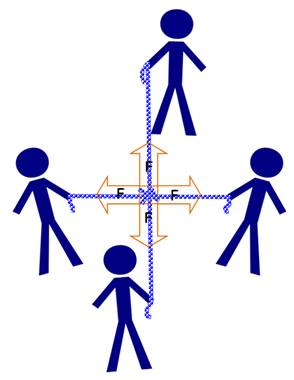
À deux fois deux Si un autre couple s'adonne à ce jeu, nous aurons deux nouvelles forces qui s'équilibrent. Un défi à quatre, maintenant. Les deux cordes sont perpendiculaires et nouées au centre. L'équilibre est réalisé si les quatre forces: sont perpendiculaires, ont une intensité égale, et s'opposent deux à deux.
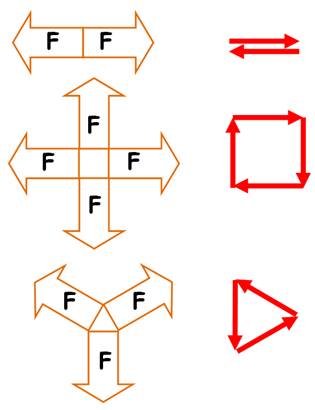
À trois Chacun des individus est placé au sommet d'un triangle équilatéral. Il est facile d'admettre que pour maintenir sa position au sommet du triangle, chacun doit tirer avec la même force. Les trois forces sont de même intensité, et orientés à 120° l'une par rapport à l'autre.

La somme des forces
Une force est symbolisée par un vecteur (un segment orienté): sa longueur représente l'intensité de la force (exprimée en newtons), son orientation indique la direction de la traction, et son sens, la direction. L'extrémité sans flèche correspond au point d'application de la force.
Pour chacun des jeux de cordes ci-dessus, amusons-nous à mettre les vecteurs de forces les uns à la suite des autres (en rouge à droite). Constat: dans les trois cas, le parcours le long des flèches (des vecteurs de force) est un circuit fermé. on revient au point de départ. La somme des vecteurs de force est nulle.	Condition d'équilibre: Somme des vecteurs nulle.

Voici maintenant deux cas typiques d'application.

Cas de la barre inclinée
On revient sur le cas de la barre inclinée. Deux forces, l'une horizontale et l'autre verticale, tirent sur une barre qui peut pivoter à l'autre extrémité. L'équilibre est réalisé lorsque la somme des forces (des vecteurs) est nulle (dessin bleu de droite). La force de résistance suit la direction de la diagonale du rectangle (en général du parallélogramme) formé par les vecteurs F1 et F2. D'ailleurs, la dite diagonale représente la somme des vecteurs F1 et F2.	Condition d'équilibre:

Cas du plan incliné
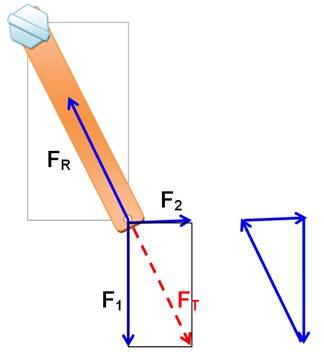
On revient sur le cas du plan incliné. La bille tend à descendre la pente sous l'effet de son poids (P). La force F maintient l'équilibre. En fait, le poids P produit deux effets: Faire descendre la bille avec la force Pi, et Appuyer sur le plan incliné avec la force Pj. L'équilibre est réalisé si la force F compense la contribution du poids Pi à faire descendre la bille. On remarque bien que la somme des deux contributions Pi et Pj est égale à P.	Condition d'équilibre: Contribution du poids:

---

Retour	Levier
Suite	Travail d'une force
Voir	Archimède – Biographie Archimède et ses contemporains Histoire Euréka Multiplication Sciences – Index
Aussi	Dicomot
Livre	Petite logique des forces; Constructions et machines – Paul Sandori – Points Sciences – 1983 Livre très abordable par tous.