|
|||||||||||||||||||||||||||||||||||
![]()
|
NOMBRE CHROMATIQUE Quantité de couleurs pour
colorer une carte, un objet … Définition et exemples. |
|
|
||
|
Nombre
chromatique K: plus petit nombre de couleurs permettant de
colorier tous les sommets d’un graphe sans que deux sommets adjacents du
graphe soient de la même couleur. |
Propriétés Quadrilatère: K = 2; Triangle: K = 3; Quadrilatère
complet: K = 4. Complet veut dire:
avec toutes ses diagonales. |
|
|
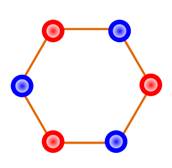
K = 2 |
Rappel: un sommet ne
doit pas être relié à un sommet de même couleur. |
|
K = 3 |
Le double pentagone (en bas à droite) est le graphe
de Petersen, un graphe souvent utilisé pour illustrer la théorie des
graphes. |
|
K = 4 |
Remarque importante: tous les graphes présentés
ci-dessus sont planaires. Ils peuvent être
représentés par un graphe sans croisement. Exemples avec les trois derniers:
Le graphe ci-dessous ne peut pas être colorié avec trois
couleurs (à gauche les verts se font face!). Résolution avec une quatrième couleur
au centre. À droite, une représentation de la carte correspondante.
|
|
K = 5 |
Remarque importante: ce graphe n'est pas planaire. Voir
Les trois maisons |
Amusement: couleurs remplacées par des nombres
|
Le problème consiste à
placer des nombres aux sommets, tels que la différence en valeur absolue soit
supérieure à un nombre k. Ici, l'exemple avec le
graphe de Petersen (vu ci-dessus),
en exigeant une distance k supérieure à 2. Cette illustration montre la
solution optimale. |
Voir Jeux
et énigmes
![]()
|
Retour Suite |
|
|
Voir |
|
|
DicoNombre |
|
|
Sites |
|
|
Cette page |
http://villemin.gerard.free.fr/aMaths/Topologi/aaaGraph/Chromat.htm
|
![]()