|
||||||||||||||||||||||||||||||||||||
![]()
|
|
QUADRILATÈRES Propriétés générales et divers types de
quadrilatères. Définition Polygone à quatre côtés ou Quadruplet de points de l'espace, non alignés trois à trois. Étymologie latine Quatuor,
quatre et latus, lateris, côté. Étymologie grecque Tétragone:
quatre angles, ou Tétrapleure:
quatre côtés Anglais Quadrilateral or complete
quadrilateral |
|
|
|
|
||
|
Plan |
Gauche |
|
|
Les
quatre points sont dans le même plan. |
Quadrilatère
non plan: les quatre points sont dans l'espace. |
|
|
Convexe |
Concave |
|
|
Tous
les sommets sont dans le même demi-plan formé avec
chacun des côtés. Exemple
ici avec le jaune. |
Non
convexe: certains sommets sont rentrants; certains côtés prolongés coupent le
quadrilatère. |
|
|
Croisé |
Complet |
|
|
Deux
côtés sont sécants. |
Les
côtés sont prolongés. |
|
Famille des quadrilatères en un clin d'œil

|
|
||||
|
|
PARALLÈLE |
PERPENDICULAIRE |
ÉGALITÉ |
|
|
Diagonales |
|
|||
|
Q. Quelconque Quadrilateral |
|
Pseudo-carré ou
Cerf-volant Kite |
||
|
Parallèles |
|
|||
|
Trapezium, trapezia (trapezoid -
US) |
T. Rectangle Rectangle
trapezium (trapezoid) |
T. Isocèle Isosceles
trapezium (trapezoid) |
||
|
Égalités |
|
|||
|
Parallelogram |
Rectangle |
Rhombus,
rhombi |
||
|
Tout ! |
Carrés = Rectangle
et Losange à la fois Square |
|
||
|
Rectangle + Côtés égaux |
Losange + Angle droit |
|||
|
|
||
|
|
|
|
Voir Autres propriétés de angles du
quadrilatère / Sommes des angles des polygones / Somme des angles opposés
|
|
||
|
Énoncé Points O1
et O2 avec O1O2 = 3 cm Cercles de centre O1 et O2 et
de rayon 4 cm Ils se
coupent en P1 et P2. Nature du quadrilatère O1P1O2P2
? Les
quatre côtés sont des rayons de même mesure: c'est un losange. Dans un losange les diagonales (O1O2)
et (P1P2) sont perpendiculaires. Bissectrice (P1P2) ? Le
triangle O1P1O2 est isocèle: ses angles à la
base sont égaux. Les
triangles rectangles
O1P1H et HP1O2 sont
égaux (2 côtés et un angle de mêmes
mesures). Les angles en P1 sont égaux. La droite
P1P2 est bissectrice de l'angle
O1P1O2. |
|
|
|
|
||
|
Un air de théorème
de Pythagore, mais appliqué au quadrilatère, et ce théorème est dû à
Euler: a² +
b² + c² + d² = m² + n² + 4u² Précisions: AC = m et BD =
n. |
|
|
|
Théorème Pour tout quadrilatère, la somme des carrés des
côtés est égale à la somme des carrés des diagonales plus quatre fois le
carré du segment joignant les milieux des diagonales. |
Anglais In any quadrilateral, the sum of the
squares of the four sides equals the sum of the squares of the diagonals plus
four times the square of the line connecting the midpoints of the diagonals. |
|
|
|
||
|
Les milieux des côtés;
Le
théorème des points
milieux dans le triangle permet de démontrer cette propriété.
|
Le quadrilatère ayant pour sommet les milieux des côtés d'un
quadrilatère quelconque est un parallélogramme. Chaque côté est parallèle à
l'une des diagonales. |
|
|
Exemples
|
||
|
|
||
|
Lorsque
le triangle OBC pivote autour de O, les diagonales restent perpendiculaires. Lorsque
BC devient parallèle à AD, les diagonales sont confondues avec les cotés des
triangles. |
|
|
|
|
||
|
Les sommets forment un quadrilatère.
|
|
|
|
|
||
|
Il suffit de cinq points (n = 5) au moins. |
|
|
|
Démonstration
avec cinq points
|
||
|
Généralisation
avec n points
Formulation
du théorème Pour tout
entier k donné, il existe un
entier n, tel que tout ensemble de
n points ou plus placés sur le
plan en position quelconque (c'est-à-dire sans que trois points soient
alignés) contient un sous-ensemble de k
points déterminant les sommets d'un polygone convexe (pouvant contenir
d'autres points).
|
||
Voir Graphes
Sujet traité par Pour la Science N°376
– Février 2009
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
La
donnée d'une diagonale permet de caractériser la quadrilatère >>> |
||
Voir Calcul de l'aire du quadrilatère
quelconque
|
– Carnot's Polygon Theorem |
|
|
|
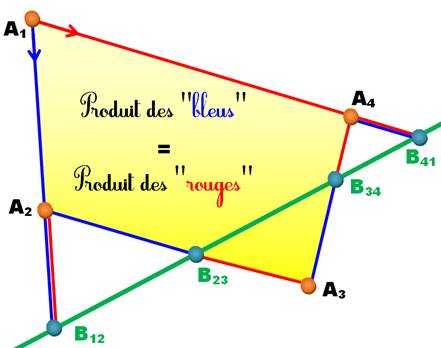
Une sécante B12B41
Il en existe deux jeux selon
que, partant du premier sommet, on se dirige dans un sens ou dans l'autre.
Ces deux produits sont égaux.
|
Illustration
Propriété
du produit des longueurs valable pour tout polygone. Formulation
|
|
Voir Lazare Carnot
|
|
||
|
Définition Un quadrilatère (convexe)
complet inclut ses côtés prolongés. C'est aussi la figure de
géométrie plane constituée
|
Quadrilatère
complet avec ses trois diagonales (bleues)
Quatre
droites, six sommets et trois diagonales. |
|
|
Droite
de Newton Les milieux M, N et O des
trois diagonales. Ces trois points sont
alignés. La droite passant par ces
trois points est la droite
de Newton. |
Quadrilatère
complet avec milieu des diagonales
Les
milieux des diagonales sont alignés. |
|
|
Relation
harmoniques Chaque diagonale coupe les
deux autres (I, J et K). Les quatre points sur chaque
diagonale sont dans des rapports harmoniques.
|
Intersections
des diagonales entre elles
Les
quatre points sur chaque diagonale sont dans un rapport harmonique. |
|
|
Construction Un
quadrilatère convexe quelconque. Les
côtés opposés sont partagés en trois segments égaux. Propriété L'aire
de chacun des trois quadrilatères (bleus et vert) est égale à un tiers des celle
du quadrilatère complet.
Voir Démonstration |
|
|
|
|
||
|
Les
quatre bissectrices des angles aux sommets se coupent en quatre points
cocycliques (sur un même cercle). The four angle bisectors of a quadrilateral
intersect adjacent bisectors in four concyclic points. |
|
|
|
|
||
|
Un
quadrilatère convexe quelconque. Les
milieux des côtés: E, F, G et H. Le quadrilatère EFGH est un parallélogramme.
Son périmètre est égal à la somme des longueurs des deux diagonales et
son aire est moitié de celle du quadrilatère. L'aire est aussi égale à la
somme des aires des quatre triangles périphériques. Les médianes EG et FH se
coupent en M. Les milieux
des diagonales D1 et D2. Ces trois points sont alignés. Notez les parallélogrammes: FD1HD2. La
démonstration de l'alignement repose sur la propriété de leurs diagonales
concourantes. |
|
|
Voir Aires des quatre quadrilatères formés
par les bi-médianes
|
|
||
|
Un
quadrilatère convexe quelconque (bleu). Les médiatrices des côtés,
prolongées d'une longueur égale au demi-côté (traits bleus).Soit, quatre
points (bleus) Les deux droites (rouges) réunissant ces quatre points, deux, à deux,
sont perpendiculaires et de même longueur. |
|
|
|
|
||
|
Théorème Parmi
cinq points quelconques du plan (donc non alignés), il est toujours possible
de tracer un quadrilatère convexe. Généralisation: on peut toujours trouver un polygone convexe de n points parmi un
nombre suffisants de points: f(3) = 3, f(4) = 5, f(5) = 9, f(6) = 17. Valeurs
inconnues au-delà. Historique Le nom a été donné par Paul Erdös du
fait qu'il a conduit au mariage conclu entre George Szekeres et Esther Klein. |
f(4) = 5 Un quadrilatère convexe existe parmi 5 points. |
|
Voir Nombres de croisements d'un graphe
![]()
|
Données A4 = 243 m²
et A8 = 305 m² Valeurs des autres? Principe
du calcul 1) Les aires A1,
A2 … A8 sont en progression arithmétique. Connaître
deux valeurs permet de calculer les autres. 2) La progression
arithmétique pour les quadrilatères sera prouvée en montrant que les
aires des deux types de triangles T1 et T2 sont elles-mêmes en progression
arithmétique. |
|
|
|
Progression
arithmétique On considère les triangles en jaune qui partagent les parcelles en deux par une
de ses diagonales. On trace les parallèles à AB en chaque
point de découpe sur CD. Elles permettent de tracer une des
hauteurs de chaque triangle jaune. |
Triangles
T1 Aire triangle T11
= base x hauteur = x . H Aire triangle T12
= x . (H + h2) Aire triangle T13
= x . (H + h2 + h3) Du fait des parallèles
espacées également de la quantité y, nous avons: h2 = h3 = h. L'aire des triangles jaunes
progresse comme: x(H), x(H+h), x(H+2h), x(H+3h), … x(H+7h), Triangles
T2 La même démonstration
s'applique et les aires des T2 sont également en progression
arithmétique. Quadrilatères
(ou Parcelle de champ) La somme des aires de T1 et
T2, l'aire des parcelles, est elle-aussi en progression arithmétique. |
|
|
Valeur
des aires Les deux valeurs indiquées vont servir à
étalonner la progression et à trouver les autres aires:
|
||
|
Internet? L'énigme
a circulé sur Internet avec dans l'énoncé un indice supplémentaire: l'aire
totale du champ est égale à l'année de la mort du paysan. Sans intérêt, sinon
de conforter le calcul. On trouve effectivement 2006. |
Une solution erronée circule sur Internet. Elle
considère les huit quadrilatères et le supplément de surface pour chacun.
Celui-ci est découpé en deux: des triangles soi-disant égaux et des losanges
soi-disant égaux. La figure est trompeuse: les droites ah et bi,
par exemple, ne sont pas du tout parallèles. |
|
Retour / Énigme
de la quatrième parcelle
![]()
|
Suite Quadrilatères |
… / Carrés ______________________________________________________________________
|
|
|
Voir |
|
|
|
DicoNombre |
|
|
|
Sites |
|
|
|
Cette page |
http://villemin.gerard.free.fr/Wwwgvmm/Geometri/Quadrila.htm |
|
![]()