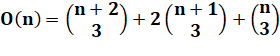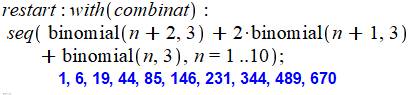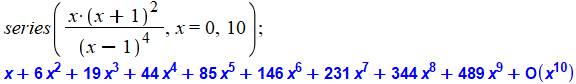|
Édition du: 25/02/2023 |
|
INDEX Types de nombres figurés: liste
et liens |
Nombres Polygonaux |
|||
![]()
|
NOMBRES OCTAÉDRIQUES Nombres
construits en déposant (en empilant)
des points (des billes, des oranges … ) de part et d'autre d'une base carrée. |
||
|
|
Sommaire de cette page >>> Caractéristiques >>> illustrations >>> Liste des nombres octaédriques >>> Nombres octaédriques
centrés ou de Haüy |
Débutants Nombres
figurés ou
géométriques Glossaire |
En bref
|
Octaédrique |
1,
6, 19, 44, 85, 146, 231, 344, 489, 670 |
|
Octaédrique centré ou de Haüy
|
1,
7, 25, 63, 129, 231, 377, 575, 833, 1159 |
|
Octaédrique tronqué |
1,
38, 201, 586, 1289, 2406, 4033, 6266, 9201, 12934 |
|
|
|||
|
Famille |
|
||
|
Définitions |
NOMBRE OCTAÉDRIQUE Nombre
formé à partir d'un octaèdre.
Empilement
de deux pyramides
successives à base carrée. |
||
|
Formule |
n > 0 |
||
|
Autres formules |
O(n) = 1² + 2² + … + (n-1)² + n² + (n-1)² + … + 2² + 1² Exemple
Exemple
de programmation
Exemple
de calcul
|
|||||||||||||||||||||||||||||||||||||||||||||||||||
|
Relation |
L'octaèdre
complété de quatre tétraèdres sur ses faces son adjacentes créé un tétraèdre
dont le volume est deux fois celui de l'octaèdre. O(n) + 4T(n-1) = T(2n-1) Exemple O(5) + 4T(4) = T(29) 85 + 4 x 20 = 165 |
|
||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
Propriétés |
En 1850 - Sir Frederick Pollock: conjecture que chaque entier positif est la
somme d'au plus sept nombres octaédriques. En chimie, les nombres octaédriques ou nombres magiques
sont utilisés pour décrire les nombres d'atomes dans les amas octaédriques. |
Voir Coefficients
binomiaux / Fonction
génératrice
|
|
|||
|
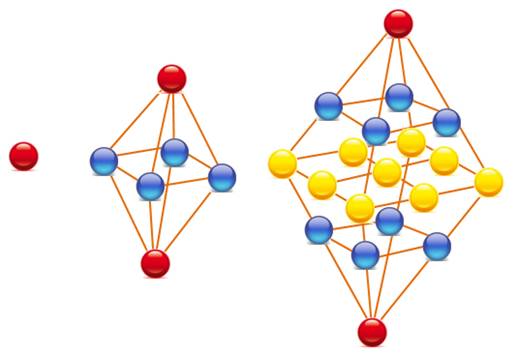
Nombres
octaédriques 1, 6, 19 Notez le
point central sur la couche jaune pour le troisième octaédrique. Chaque
bille bleue s'empile sur quatre billes jaunes. |
|
||
|
Représentation
sous forme de cubes pour le nombre octaédrique 6 |
|
||
|
|
|||||||||||||||||
|
0, 1, 6, 19, 44, 85,
146, 231, 344, 489, 670, 891, 1156, 1469, 1834, 2255, 2736, 3281, 3894, 4579,
5340, 6181, 7106, 8119, 9224, 10425, 11726, 13131, 14644, 16269, 18010,
19871, 21856, 23969, 26214, 28595, 31116, 33781, 36594, 39559, 42680, … |
|||||||||||||||||
|
Somme des couples successifs de nombres pyramides-carrés
|
|||||||||||||||||
|
|
|||
|
Octaédrique centré ou de Haüy
|
1,
7, 25, 63, 129, 231, 377, 575, 833, 1159 |
||
|
Liste 1, 7, 25, 63,
129, 231, 377, 575, 833, 1159, 1561, 2047, 2625, 3303, 4089, 4991, 6017,
7175, 8473, 9919, 11521, 13287, 15225, 17343, 19649, 22151, 24857, 27775,
30913, 34279, 37881, 41727, 45825, 50183, 54809, 59711, 64897, 70375, 76153,
82239, … |
|
||
|
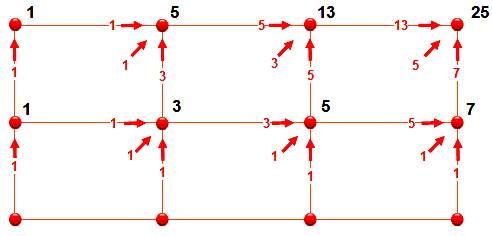
Ces nombres représentent la quantité de façons d'aller
du bas-gauche vers le haut-droit en progressant continument en horizontal
vertical ou oblique dans une maille d'une grille de (n-1, 3). Ici, les 25 façons pour n = 3, soit la grille (2, 3). Cas particulier des nombres
de Delannoy avec une largeur fixe de 3. |
|
||
Voir Réseaux et chemins sur réseaux
![]()
|
Voir |
|
|
DicoNombre |
|
|
Sites |
|
|
Cette page |
![]()