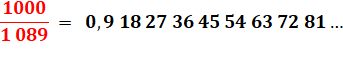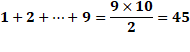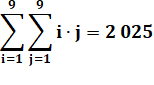|
|||||||||||||||||||||||||||||||||||||
![]()
Humour
|
Toto, très entreprenant, déménage la salle de classe. – Pourquoi tu fais cela, Toto? – Ben, madame, vous avez demandé d'étudier les multiplications sans les tables. |
Voir Pensées & humour
|
Ajoutez tous les nombres de la table
de multiplication des nombres de 1 à 9.
Quelle est la somme ? Trouvez l'astuce de calcul ! |
|
TABLES de MULTIPLICATION L'apprentissage des
tables est terriblement fastidieux! Comment les
apprendre une bonne fois pour toute. Avec méthode,
logique. Et les imprimer
définitivement en mémoire. Hep! Il faut tout
de même fournir un petit effort … ! Attention: Les explications sont
détaillées et semblent un peu longues. Mais une fois assimilée, la méthode
est simple. Habituez-vous à reconstruire la
table dans l'ordre de la présentation ou adoptez vos propres variantes si
cela vous semble plus facile. |
|
Orientation Je souhaite voir les TABLES tout de
suite >>> Je souhaite connaitre la méthode
d'apprentissage en bref >>> Ou plutôt, pas à pas >>> |
Voir Table de
multiplication originale / Brève 69
– Multiplication / Table en DicoMot Math
|
|
||
|
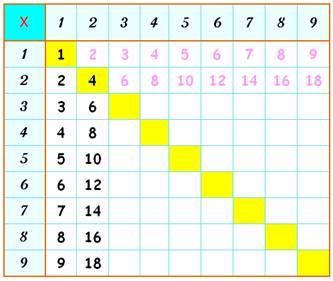
Voici le tableau que nous allons utiliser (table
de Pythagore). On lit le résultat de la multiplication à l'intersection des
lignes et des colonnes. Par exemple: 4 x 4 = 16 Rappel: le résultat d'une
multiplication s'appelle le produit. |
|
|
|
C'est un
tableau qui comporte 9 x 9 = 81 cases de
résultats. Soit 81 valeurs de produits à
apprendre. Table formée de 9 cases le long de la diagonale (jaune) et de deux
triangles de 36 cases de part et d'autre de cette diagonale. |
|
|
||
|
|
Chouette! La
table est symétrique. On retrouve
deux fois les mêmes résultats. (Sauf sur la diagonale) Inutile de
retenir les cases du haut à droite (en rose) |
|
|
Nous pouvons
éliminer le triangle supérieur de 36 cases qui donne les mêmes résultats que
ceux du triangle en bas à gauche. Éliminons tout de suite également la
colonne (9 cases) de la multiplication par 1 qui est si évidente. Restent 81
– 36 – 9 = 36
cases à apprendre. |
|
|
|||
|
|
||
|
Nous venons de
placer les premières huit valeurs intéressantes pour la table. Restent 36 – 8
= 28 cases à apprendre. |
|
|
|||
Formons
la ligne 5, 10, 15, 20, 25, 30, 35, 40 et 45. Par
effet miroir, écrivez les résultats dans la colonne en dessous du 25. |
Entr 5 fois 2 égal 10; 5 fois 3 égal 15 … |
||
|
Nous venons de
placer 7 nouvelles valeurs dans la table Restent 28 –
7 = 21
cases à apprendre. |
|
|
|||
Les enfants curieux adorent ce truc!
|
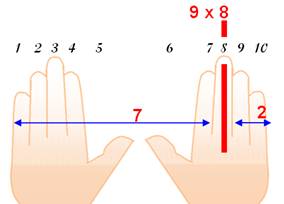
Table du neuf facile! Observez cette belle symétrie,
comme dans un miroir:
Complétons la table
|
||
|
Magie
du nombre
1089:
Division qui donne
la table de multiplication par 9. |
Voir Magie
– Index
|
Nous venons de
placer 6 nouvelles valeurs dans la table Restent 21 –
6 = 15
cases à apprendre |
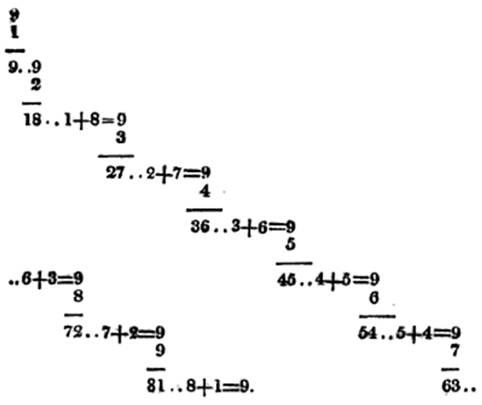
Histoire: présentation
et observations datant des années 1600
|
L'auteur observait: la
somme des chiffres des produits est égale à 9. Ces chiffres se répètent dans
l''odre inverse après le 5. La somme des produits de
1 à 9 par 9 est égale à 405 et, divisée par 9, elle vaut 45. La somme de tous
les chiffres de ces produits est 81 = 9² La somme des produits et des
chiffres est égale à 405 + 81 = 486
qui, divisé par 9 donne 54 avec 5 + 4 = 9. Avec neuf cloches, il y
a 9! = 362 880 possibilités (permutations)
de sons possibles. La somme des chiffres est 27 et 2 + 7 = 9. Son quotient
par 9 est 40 320 et 4+3+2 = 9. |
D'après: Recreations in Mathematics and Natural
Philosophy – Jacques Ozanam
|
|
|
|
|
|
|
Problème Quelle
est la somme de tous ces nombres figurant dans la table de multiplication des
nombres de 1 à 9 ? Solution On remarque que la somme de la première colonne
est la somme des
nombres de 1 à 9 qui est égale à: Chaque des colonnes montre les mêmes nombres
multipliés par 2, 3, … 9. La somme sera: Formulation
|
Table de multiplication
Somme
des nombres de la table 1 à 9 = 45² = 2 025 Somme
des nombres de la table 1 à 10 = 55² =
3 025 |
Retour /
Brève
565 Autres énigmes
![]()
|
Suite |
|
|
Voir |
|
|
Site |
|
|
Cette page |