|
|||||||||||||||||||||||||||||
![]()
|
F |
Nombre / Diviseurs / Multiplicatif / Premiers |
|
Définition |
NOMBRES PREMIERS de STERN Nombre premier p tel que, quel que soit q,
un premier inférieur à p, on ne trouve jamais p – q = 2 b². Nombre premier qui n'est pas la somme d'un
nombre premier et du double d'un carré parfait non nul. |
|
Exemples |
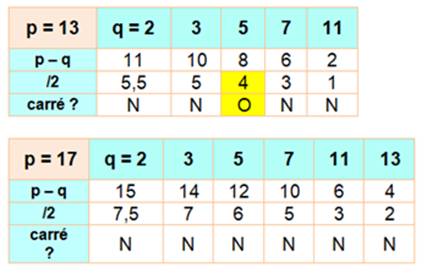
Le
nombre premier 13 n'est pas de Stern, alors que 17 l'est.
En
effet: 13 = 5 +
8 = 5 + 2 × 2² . Condition suffisante pour déclarer que
13 n'est pas un nombre premier de Stern. On a même en plus: 13 = 11 + 2 = 11
+ 2 × 1². |
|
Commentaire |
Moris
Stern (1807-1894) élève de
Gauss qui est devenu son successeur comme professeur à l'université de
Göttingen. |
|
Anglais |
A Stern prime is a
prime number that is not the sum of a smaller prime and twice the square of a
non zero integer. |
|
Nombres non- sommes d'un premier et du double d'un carré |
|
|
|
Premiers |
2, 3, 17, 137, 227,
977,
1 187,
1 493 Seuls
connus. Le
suivant, s'il existe, serait > 2 1013. |
|
|
Impairs composés |
5 777,
5 993 Seuls
connus. En 1752, Christian Goldbach fit
connaître cette conjecture à Euler:
Texte de Goldbach (18 novembre 1752)
Euler a vérifié la véracité jusqu'à
2500. Ruemmler a trouvé l'exception 5 777
en se demandant si elle était la seule. Moritz Abrahan Stern (1807-1894), professeur
de mathématique à Göttingen a testé les nombres jusqu'à 9 000 avec ses
étudiants. Ils ont trouvé les deux exceptions citées de même que la liste
complète des nombres premiers de Stern.
|
|
|
Liste complète ? |
1,
3, 17, 137, 227, 977, 1 187, 1 493, 5 777, 5 993 À
partir de 17, tous ces nombres sont congruents à 2 mod 3. À
partir de 17, tous les nombres sont en 6n – 1. Ces dix nombres sont sans doute les
seuls nombres impairs (premiers ou composés) à être de Stern: somme d'un
premier et du double d'un carré. Cela jusqu'à au moins 2 1013. Il y a de bonne raison de penser que
la liste est complète, car la quantité de présentations augmente rapidement
avec n. Voir Les
records. Hardy et
Littlewood ont émis cette nouvelle conjecture: Tout grand
nombre impair (> 6000) est la somme
d'un nombre premier et du double d'un carré. La quantité de représentations
vaut:
w
vaut pour tous les premiers et (2n/w) est le symbole de Legendre. Laurent
Hodge formule une conjecture plus forte: Pour
chaque nombre N > 1, il n'y a qu'un nombre fini d'entiers impairs qui ne peuvent
pas être représentés comme la somme d'un nombre premier et de deux fois un
carré d'au moins N façons. |
|
Curiosité
|
Vittorio
Ornago, chercheur en nombres premiers, fait remarquer cette propriété des
nombres premiers de Stern (S). Pour
les cinq compris entre 17 et 1187 on a: S = 10(n² – 3) + 7. Avec
n de 2 à 11, on retrouve ces nombres et d'autres. Tous sont premiers. Le
12e de cette forme est
1417. Il est composé et non-Stern (1417 = 13 × 109). Le
suivant est 1667. La formule ne réussit pas à capter le nombre premier de
Stern le plus grand (1493). |
|
|
|
||
|
|
Une manière de lister tous les nombres premiers Sélection des premiers parmi le nombre 2 et la suite des nombres
impairs de 3 à n. Voir Séquence |
|
|
|
Utilisation d'une liste pour définir à quels nombres s'applique la fonction (ici le carré). |
|
|
|
Programme de recherche des premiers de Stern Recherche jusque n = 20. Liste des premiers dans P. Liste des double-carrés dans C, arrêt à racine de
n. Floor est la fonction plancher. T est la liste de toutes les possibilités de
sommes d'un premier avec les double-carrés. La dernière instruction (minus) retire de P
toutes les valeurs présentes dans T. Rappel: les accolades
définissent des ensembles; les doublons sont automatiquement éliminés. |
|
Voir Programmation – Index
Idée du
programme d'après Robert Israel - OEIS A042978
|
|
||
|
|
Commentaire N recevra les nombres premiers de Stern. R est la suite des nombres en double carré. P est la suite des nombres premiers. Le témoin T est a 1 si Stern. Deux boucles pour exécuter toutes les sommes deux
à deux. Dés la présence d'une somme égale à n, alors le
témoin est mis à 0. Si le témoin résiste à 1, le nombre est de Sterne
et il est placé dans la liste N. |
|


Remarquez
que pour ces
nombres le carré impliqué ne dépasse pas 9
Exemple de lecture: 139 est le plus petit nombre sept fois sommes d'un
premier et d'un double carré.
|
1, 5 2, 13 3, 21 4, 49 5, 55 6, 91 |
7, 139 9, 181 10, 301 11, 391 12, 481 13, 559 |
14, 619 15, 829 16, 859 17, 1069 19, 1081 20, 1489 |
21, 1609 22, 1741 23, 1951 24, 2029 26, 2341 29, 3331 |
30, 3589 31, 3961 33, 4189 35, 4801 36, 4975 |
![]()
|
Suite |
|
|
Voir |
|
|
DicoNombre |
|
|
Livre |
|
|
Sites |
|
|
Cette page |
![]()