|
Édition du: 27/10/2024 |
|
INDEX |
Partitions – Goldbach |
|||
![]()
|
Conjecture de GOLDBACH - Introduction |
||
|
Terminale |
Sommaire de cette page >>> Introduction >>> Conjecture >>> Tables pour n < 25 >>> Table d'addition originale >>> Quantité de décompositions pour n < 100 >>> Fonction quantité de partitions >>> Quantité de décompositions autour de 1 000 >>> Conclusion >>> English corner |
Débutants Glossaire |
|
Conjecture de GOLDBACH La décomposition des nombres
en sommes a toujours été une source d'émerveillement, tout comme celle des
nombres en produits. Il existe une conjecture donnant une décomposition très simple
Pourtant elle n'est toujours pas démontrée. Après Fermat, la conjecture de Goldbach
est l'un des problèmes les plus importants de la recherche des
mathématiciens.
|
|
|
||
|
Nombres & Multiplication |
Nombres et Addition |
|
|
Décomposition
en produits de facteurs premiers |
Partition
en sommes de nombres premiers |
|
|
|
|
|
|
Théorème fondamental de l'arithmétique:
les nombres premiers comme briques de construction de tous les autres par multiplication. |
Conjecture de Goldbach: les nombres premiers en quantité
réduite comme briques de construction de tous les autres par addition? |
|
Voir Nombres premiers
|
|
||
|
Nombres PAIRS égal somme de deux nombres premiers pour n > 2 |
Nombres IMPAIRS égal somme de trois nombres premiers pour n > 5 |
|
|
PAIRS
|
IMPAIRS
Car tous les premiers > 2 sont impairs
et,
|
|
|
Elle est fausse pour 2
= 1 + 1 Elle est vraie pour 4 = 2 + 2 NB. les nombres premiers peuvent
être répétés. |
Elle est fausse pour 3
= 1 + 1+1 Elle est vraie pour
7 = 2 + 2 + 3 NB. Avec deux premiers, on a 5 = 2 +
3 |
|
Voir 1 n'est pas
premier
La conjecture sur les impairs est déduite de celle sur les pairs
|
Un
nombre impair plus grand ou égal à 7 (= 4
+ 3) est toujours égal à un nombre pair
plus 3. Impair = Pair + 3 Or
supposons que tout nombre pair plus grand que 4 soit somme de deux nombres
premiers. Alors: Impair = Premier + Premier + 3,
soit somme de trois premiers. Dès que c'est possible le nombre 3 peut
être remplacé par n'importe quel autre nombre premier, ce qui induit une
quantité innombrable de sommes de trois premiers pour les nombres impairs. Recherche de la preuve
|
|
Dans
un article du 31 janvier 2012 intitulé Every
odd number greater than 1 is the sum of at most five primes , Terence Tao
montre que chaque nombre impair peut s'écrire comme somme de cinq nombres
premiers au plus. En
mai 2013, Harald Helfgott prépublie sur arxiv une preuve de la conjecture. À
ce jour cette preuve n'a pas été publiée dans une revue à comité de
lecture. Voir Historique |
Voir Historique
/ Recherche de la preuve
|
|
||
|
Pair = Premier + Premier Le nombre n pair (si n > 2) est somme de deux premiers,
au moins une fois. |
|
|
|
Impair = Premier + Premier Le nombre n impair n'est pas la somme de 2 nombres
premiers. Seuls les impairs premiers séparés de 2 unités possèdent cette
propriété. Ce sont les nombres premiers
jumeaux. |
|
|
|
Impair = Premier + Premier + Premier Le nombre n
impair (si
n > 5) est somme de trois premiers, au moins une fois. |
|
|
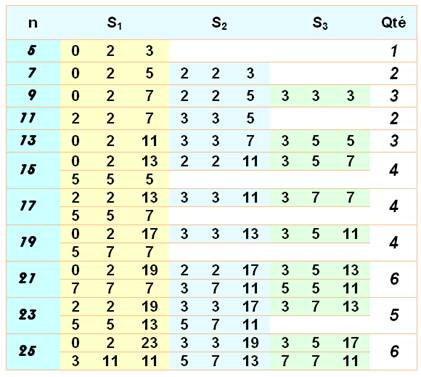
Une table d'addition originale

Voir
Suite de cette table et autres types
de représentations
|
|
|
|
Compte tenu de la quantité
croissante des partitions, on pourrait penser que la démonstration
de la conjecture ne devrait pas poser de problème. Et pourtant si! |
|
Fonction quantité de partitions
|
La
fonction qui donne la quantité de sommes pour un nombre pair (E, comme even)
est nommée r(N). Exemple:
100 = 3 + 97 = 11 + 89 = 17 + 83 = 29 + 71 = 41 + 59 = 47 + 53 soit six
possibilités. Alors r(100) = 6. Évidemment
les permutations (comme 97 + 3) ne sont pas comptées. |
Voir Comète
de Goldbach
|
|
|
|
Cas de 1 000 r(1 000)
= 28 sommes
de 2 premiers
Cas de 999 r(999) =
770
sommes de 3 premiers
Cas de 1 001 r(1 001)
= 1 095
sommes de 3 premiers
Cas de 5 779 (par exemple) 5 779 n'est pas somme de deux premiers. C'est impossible, car la
somme de deux nombres premiers est toujours paire, sauf avec 2 et 5 777 (composé:
5 777 = 53 x 103). 5 776 est la somme de deux premiers 63 fois. Donc, 5 779 = 5776 + 3
est au moins somme de trois premiers 63 fois. 5 779 est en fait la somme de trois premiers 16 886 fois. Exemples:
(3, 2 879, 2 897), (3, 2 837, 2 939) … (199, 2 039, 3 541) … (1 913, 1 933, 1
933) Note: le fait que 5 779 soit premier importe peu
pour la conjecture de Goldbach. |
|
|
Il
est assez paradoxal que la conjecture de Goldbach ne soit pas démontrée avec:
|
|
|
|
|
The Goldbach
conjecture asserts that every even integer greater than 2 is the sum of two
primes. Stated by Christian Goldbach in 1742, verified up to 1018
at least, this conjecture has evaded all attempts at proof. Ternary Goldbach
conjecture (TGC): at least it seems that every number that is greater than 2
is the sum of three primes. Strong or binary Goldbach
conjecture (BGC): all positive even integers Goldbach partition: two primes (p,
q) such that p + q = 2n for n, a positive integer. |
|
![]()
|
Suite |
|
|
Voir |
|
|
Revues |
|
|
Cette page |
![]()