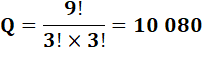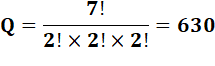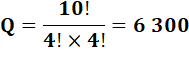|
|||||||||||||||||||||||||||||||||||||||||||||
|
Anagrammes de MISSISSIPPI sous contraintes Le nom de cette ville des États-Unis se prête idéalement au jeu
du décompte des anagrammes de ce mot. Une anagramme valable de ce
mot ne compte que 5 lettres: pipis; ou 6 lettres avec missis (mesdemoiselles) en anglais Ici, nous cherchons toutes
les possibilités d'échange des lettres. On se donnera également des
contraintes. |
Voir Mississippi en grille –
Quantité de chemins
|
|
||
|
Le mot Mississippi compte 11 lettres. La
quantité de permutations
des lettres ne présente pas d'intérêt du fait de la répétition des lettres. Il faut
chercher autre chose. |
Quantité de permutations P =11! = 39 916 800 |
|
|
La
méthode des coefficients multinomiaux
tient compte de ces répétitions. Avec 11 lettres dont 1
M, 4
I, 4 S
et 2 P. |
Quantité d'anagrammes
|
|
|
Méthode directe par élimination des
redondances (coefficients multinomiaux) On
explique la division par le calcul de la quantité des répétitions de chaque
lettre. Attention: division par la
quantité de répétitions (11! / 4!) et non soustraction (11! – 4!). De manière imagée, certains
parlent de la méthode du berger: ayant
compté les pattes des moutons, il faut diviser par 4 pour connaitre la
quantité de moutons. |
Par exemple La lettre "I" est
présente quatre fois. Tous les cas présentant une permutation de ces quatre
"I" sont identiques, donc redondants; or, ils sont au nombre de 4!
D'où la division par factorielle
4. |
|
|
Méthode alternative par les combinaisons Il s'agit
de placer:
Les actions sont indépendantes et les
possibilités se
multiplient. |
|
|
|
Comparaison des résultats obtenus
par les deux méthodes
|
||
Certains sites présentent un calcul avec MISSISSIPI
mal orthographié; évidemment le résultat est différent.
|
|
||
|
Nous
ajoutons la contrainte suivante: Pas de
PSI dans les anagrammes. |
MISSISSIPPI OUI PSIMSISSIPI NON |
|
|
Pour
éliminer les cas où le groupe PSI apparaît, on considère ce groupe comme un
tout. Au lieu de 11 objets, nous en avons maintenant 9. |
PSI, M,
S, I, S, S, I, P, I n = 9 avec 3 S et 3 I.
|
|
|
La
quantité d'anagrammes de Mississippi sans PSI serait la différence. |
34 650 – 10 080 ? |
|
|
En fait, pas
tout à fait, car nous avons encore des doublons. Il faut tenir compte des cas
où PSI est présent deux fois; pas trois, car il n'y a que deux P. |
PSIMSISSIPI OUI PSIMSISISPI NON |
|
|
Cette fois,
l'ensemble des objets à considérer compte 7 objets. |
PSI, PSI, M,
S, S, I, I n =
7 avec 2 S et 2 I
et sans oublier 2 PSI
|
|
|
Le nombre
de permutations qui contiennent le groupe PSI est la quantité de celles qui
contiennent au moins PSI, moins la
quantité de doublons. |
QPSI = 10 080 – 630 = 9 450 |
|
|
Bilan, la quantité d'anagrammes de MISSISSIPPI sans PSI
est égal à: |
34 650 – 9 450 = 25 200 |
|
|
|
||
|
Nous
ajoutons la contrainte suivante: Les deux
P sont séparés |
MISSISSIPPI NON MISSISSPIPI OUI |
|
|
Supposons
les deux P ensembles. Ce seront
des cas à exclure. |
PP, M, I, S, S, I, S,
S, I, I n =
10 avec 4 S et 4 I
|
|
|
Soit le
nombre d'anagrammes de MISSISSIPPI sans avoir PP |
34 650 – 6 300 = 28 350 |
|
|
|
||
|
Combien
de mots de quatre lettres peut-on former avec les lettres de MISSISSIPPI? On va examiner les différents cas les uns après
les autres. |
MISSISSIPPI Quatre sortes de lettres: (M1, I4,
S4, P2) |
|
|
Mots de 4
lettres, toutes différentes. |
Ce sont toutes les permutations de quatre lettres. 4! = 24 |
|
|
Mots de 4
lettres avec une lettre répétée deux fois seulement; les deux autres sont
distinctes. |
Elles sont 3: {I, S, P} 3 façons de choisir une lettre répétée. Choix des 2 distinctes parmi les 3
restantes: (3, 2) = 3. Manière de permuter ces lettres: 4! / 2! =
12. Bilan: 3 x 3 x 12 = 108 |
|
|
Mots de 4
lettres avec une lettre répétée trois fois seulement. |
Elles sont 2: {I, S} 2 façons de choisir une lettre répétée. 3 choix pour la lettre restante Manière de permuter ces lettres: 4! / 3! =
4. Bilan: 2 x 3 x 4 = 24 |
|
|
Mots de 4
lettres avec une lettre répétée quatre fois. |
Elles sont 2: {I, S} Les deux possibilités sont IIII et SSSS |
|
|
Mots de 4
lettres avec deux lettres distinctes répétées deux fois. |
Elles sont 3: {I, S, P} 3 façons de les choisir Manière de permuter ces lettres: 4! / (2! x
2!) = 6. Bilan:
3 x 6 = 18 |
|
|
Bilan Quantité
de mots de 4 lettres possibles avec les lettres de MISSISSIPPI. |
24 + 108 + 24 + 2 + 18 = 176 |
|
|
Voir |
|
|
Aussi |
|
|
Cette page |
