|
Édition du: 05/06/2023 |
|
INDEX |
Aire des polygones |
||
Faites un double-clic pour un retour en haut de page
![]()
|
Théorème de Pick
Georg Pick (1859-1942) –
Mathématicien autrichien, il énonce ce théorème en 1899. Formule de Pick: A = P/2 +
Q – 1 P = quantité de
points sur la frontière (le périmètre), et Q = quantité de
points à l'intérieur de la frontière. La formule
donne bien la valeur réelle de l'aire, pas une simple approximation. |
||
|
|
Sommaire de cette page >>> Approche avec le rectangle >>> Cas du triangle quelconque >>> Exemples de figures particulières >>> Cas des polygones réguliers >>> Pourquoi ça marche – Intuitivement >>> Démonstration par récurrence >>> Aire sous les entiers du cercle >>> Bilan >>> Anglais |
Débutants Glossaire |
Mots clés
Voir Lexique
|
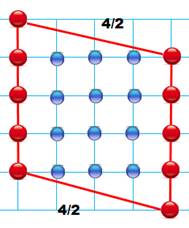
Aire du rectangle Longueur: a = 4 Largeur:
b = 3 Aire:
A = 3 × 4 = 12. Formule de Pick 1.
Compter
les points rouges: P = 14; 2.
Compter les
points bleus: Q = 6; 3.
Appliquer
la formule: A = P/2 +
Q – 1 Conclusion La formule s'applique bien au rectangle et nous
en avons la démonstration (ci-contre). |
Figure
Calcul et démonstration P = 2a + 2b = 2x4 + 2x3 = 14 Q = (a – 1)(b – 1) = 3 x2 = 6 Formule de Pick: A = (a + b) + ab – a – b + 1 – 1 = ab Ce qui est bien l'aire du rectangle. |
|
Voir Brève
876
|
Aire du triangle rectangle Base: a = 4 hauteur: h = 3 Aire: A =
½ (3 × 4) = 6. Formule de Pick 1.
Compter
les points rouges P = 8; 2.
Compter
les points bleus Q = 3; 3.
Appliquer
la formule; A = P/2 +
Q – 1 Conclusion La formule s'applique bien au triangle rectangle
et nous en avons la démonstration. |
Figure
Calcul littéral P = a + h + 1 = 4 + 3 + 1 = 8 Q = ½ (a – 1)(h – 1) = ½ x 3 x2 = 3 Formule de Pick: A = ½ (a + h + 1) + ½ (a – 1)(h – 1) – 1 Ce qui est bien l'aire du triangle rectangle. |
|
|
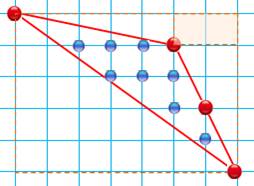
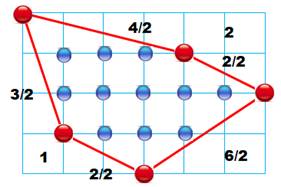
Aire du triangle rectangle Le rectangle enveloppe est tel que deux sommets
au moins sont sur la frontière du rectangle.
Grand rectangle: 7 x 5 = 35 Petit rectangle: 2 x 1 = 2 Triangles rectangles: ½ (7x5) + ½ (2x4) + ½ (5x1)
= 24 Aire du triangle : A = 35 – 2 – 24 = 9 Formule de Pick 1. Compter les points rouges P = 4; 2. Compter les points bleus Q = 8; 3.
Appliquer
la formule; A = P/2 +
Q – 1 Conclusion La formule s'applique à ce type de triangle et
nous en avons la démonstration. |
Démonstration Le théorème de Pick s'applique au rectangle
enveloppe et au petit rectangle comme aux triangles rectangles à retirer; il
s'applique au triangle interne. Si le sommet interne est lui aussi sur la
frontière du rectangle, le petit rectangle disparait et le théorème de Pick
s'applique toujours. |
|
Nous savons que …
|
Il nous faut démontrer qu'elle est valable pour
tout polygone. Or, tout polygone se décompose en triangles ayant
des côtés communs. Voyons d'abord le cas de figures particulières. |
|
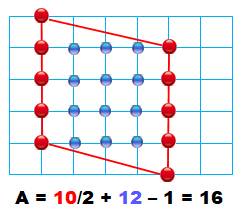
Parallélogramme L'aire de ce parallélogramme est égale au produit
de la base par la hauteur: A = 4 × 4 =
16 Autre méthode: Formule de Pick 1.
Compter
les points rouges P = 10; 2.
Compter
les points bleus Q = 12; 3.
Appliquer
la formule; A = P/2 +
Q – 1 |
|
|
|
Pentagone quelconque L'aire de ce pentagone est égale à: Formule de Pick 1.
Compter les
points rouges P = 5; 2.
Compter
les points bleus Q = 11; 3.
Appliquer
la formule; A = P/2 +
Q – 1 |
|
|
|
Pentagone régulier (figure du haut) Côté: 4 Aire:
Avec la formule de Pick En principe non applicable puisque les sommets du
pentagone ne peuvent pas être sur un quadrillage (aussi fin soit-il; voir le
théorème qui suit). Aire: A = 8/2 + 23 – 1 = 26 Pentagone irrégulier (figure du bas) Aire : = 36 – 6
– 4 = 26 Avec la formule de Pick Applicable puisque les sommets de ce pentagone
sont sur la quadrillage Aire: A = 8/2 +
23 – 1 = 26 Théorème Sauf pour le carré, pour tout polygone régulier, y
compris le triangle équilatéral, les coordonnées d'au moins un sommet sont
irrationnelles Sauf pour le carré, la formule de Pick est
inapplicable. Voir Démonstration |
Pentagone régulier: trois points hors du
quadrillage, formule de Pick non applicable.
Pentagone sur le quadrillage (non régulier):
formule de Pick bien applicable. |
|
|
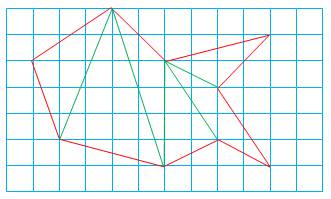
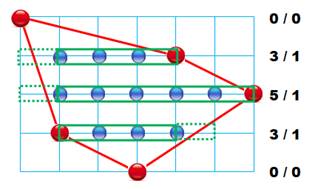
Calcul de l'aire par tranches Une méthode courante pour évaluer l'aire d'une
figure consiste à découper cette figure en tranches. Les tranches vertes (figure) couvrent une surface interne à la figure. Leur aire vaut
11, c'est une aire par défaut. Ajouter les compléments (pointillés verts) donne
une aire par excès: 11 + 3 = 14 La moyenne ne doit pas être loin de la vérité:
(11 + 14) / 2 = 12, 5. |
Aire de la figure: 12,5. Moyenne "défaut + excès" = 12, 5. |
|
|
Principe Nous savons que la formule est vraie pour tout
type de triangle. Or, un polygone peut toujours être triangulé. Soit un triangle ou un polygone. Il est complété
par un triangle externe (T) ayant un côté commun avec la figure initiale
(Pi). En supposant la formule vraie pour une figure
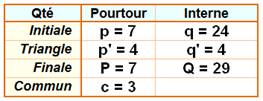
initiale, montrer qu'elle est vraie pour la figure étendue (Pf). Notation des quantités de points
Avec c, la quantité de points sur le côté commun,
dont deux sont des sommets. |
Figure initiale: Ai = 7/2 + 24 – 1 = 26,5 Figure étendue: Af = 7/2 + 29 – 1 = 31,5 |
|||||||||||||||||||||||||
|
Démonstration par récurrence de: Si
la formule est vraie pour un triangle, elle est vraie pour deux triangles accolés Or,
elle est vraie pour un triangle. Elle
est donc vraie pour toute figure formée par la réunion de triangles.
Ce qui montre que, si la formule est vraie pour
un triangle ou un polygone, elle est vraie pour le même triangle ou polygone
complété d'un triangle. Or elle est vraie pour tout triangle isolé. Elle
est donc vraie pour toute figure formée de triangles accolés comme les
polygones. |
||||||||||||||||||||||||||
Voir Démonstration
par récurrence / Brève de
maths n°1
|
Problème Calculer
l'aire du polygone dont tous les sommets sont les points "entiers"
sur le cercle de rayon 10. "Entiers" = nombres entiers pour les coordonnées
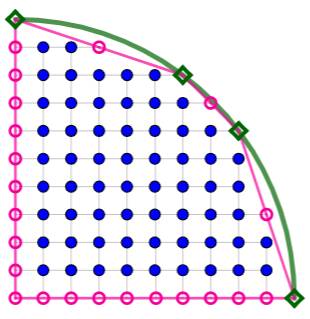
des points. Pistes Le
calcul sur un quart de cercle suffit. Alors,
il n'existe que quatre points "entiers" sur ce quart de cercle: (0,
10), (4, 9), (9, 4) et (10, 0) Théorème de Pick On
note tous les points "entiers" du polygone. En vert ceux sur le
cercle; en rose les points en périphérie et en bleu les points internes. Quantité
de points sur le bord: 26. Quantité
de points internes: 62 Formule
de Pick: A = 26/2 + 62 – 1 = 74 Aire demandée: A = 74 Vérification avec rectangles et triangles A
= 6×8
+ 6×3
+ 2×6/2
+ 2×2/2
+ 6×2/2
= 74 |
|
|
D'après Hervé
Clavier – Quora
|
La formule de Pick est plus amusante que
pratique; en tout cas bien originale ! Sa démonstration est élémentaire. Il existe
d'autres démonstrations. Et surtout, le théorème est généralisable. Vous
trouverez ces développements dans l'article de Jean-Paul Delahaye, cité en
référence, et disponible dans les bonnes bibliothèques. Notez que dans le cas de polygones à trous:
appliquer la formule au polygone et au trous et faites la différence. |
|
Pick's theorem gives an elegant formula for the area
of simple lattice polygons. Polygons covered by the theorem have their
vertices located at nodes of a square grid or lattice. Pick’s Theorem provides a method to calculate the
area of simple polygons whose vertices lie on lattice points—points with integer
coordinates in the x-y plane. The word “simple” in “simple polygon” only
means that the polygon has no holes, and that its edges do not intersect. To compute the area of a simple polygon with the
formula, we will only need to know the number of interior points (the points
of the grid that are inside the polygon) and the number of boundary points
(the points of the grid that lie exactly in the boundary of the polygon). |
Voir
Anglais pour le bac et pour les affaires
![]()
|
Retour |
|
|
Suite |
|
|
Voir |
|
|
Livre |
|
|
Sites |
|
|
Cette page |
http://villemin.gerard.free.fr/GeomLAV/Polygone/ThdePick.htm
|