|
|||||||||||||||||||||||||||||
![]()
|
OU MENTIR Il
existe de nombreuses énigmes impliquant
Certains de ces problèmes ne sont
pas évidents à résoudre. Il est important de bien poser les hypothèses. |
|
Dans Don Quichotte: À
la frontière d'un pays, il faut dire la vérité sinon c'est la pendaison |
Q - Pourquoi
venez-vous ? R - Pour être pendu ! … |
Voir Pensées & humour
/ Interdictions
|
|
|
|
Deux
copains savent que l'un est menteur et l'autre est véridique. Si
je dis à l'un d'eux: "ton copain dit la
vérité, n'est-ce pas?". Que
croyez-vous qu'il me réponde?
Cette
question ne permet pas de détecter qui est qui, car les deux répondent non.
Quelle est la question qui pourrait détecteur la qualité de chacun? Ce
serait: "si je demandais à votre copain s'il
est menteur, quelle serait a réponse?"
Celui
qui répond OUI est le menteur et celui qui répond NON est le véridique. |
|
Niveaux de raisonnement logique
|
Une personne Deux personnes
|
![]()
Deux personnes vous interpellent
|
Parmi
deux personnes, véridiques ou menteuses,
l'une dit: "Au moins l'un de nous est menteur". Déduction? Si
la personne était menteuse, son affirmation serait vraie; il serait donc
védique. Contradiction, donc pas possible. Donc
la personne est véridique et l'autre est menteuse. |
Énigmes
|
|
||
|
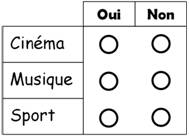
Situation Dans
la salle: 20 personnes Trois
catégories: les adeptes de cinéma, ceux de musique et ceux de sport. Ils
y ceux qui disent toujours la vérité et ceux qui mentent. Combien
sont menteurs? |
Sondage:
quel est votre passion? Cocher oui ou non pour chaque rubrique:
12
cochent cinéma, 5 musique, et 8 sports |
|
Voir Solution
|
|
||
|
Situation Albert
est véridique lorsqu'il est joyeux, menteur autrement. Bernard
est menteur lorsqu'il est joyeux, menteur autrement. |
Systématiquement
l'un est joyeux lorsque l'autre est triste. |
|
|
Énigme Comment reconnaître Albert et Bernard à
coup sûr? |
||
Voir Solution
|
|
||
|
Situation Deux gardiens de prison: L'un
dit la vérité, et L'autre
ment toujours. |
Deux portes en face du prisonnier: l'une
donne la liberté, et l'autre
la prison. |
|
|
Énigme Le prisonnier a une chance de se retrouver
libre en choisissant la bonne porte Pour cela, il a le droit de poser
une question unique aux gardiens. Il en existe effectivement au moins une qui
lui donnera la liberté Laquelle ? |
||
Voir Solution / Le dilemme du prisonnier
|
|
||
|
Situation Deux
personnes Albert et Bernard |
L'un
(Véridique) dit toujours la vérité et l'autre (Menteur) ment toujours. |
|
|
Énigme Cédric interroge Albert mais ne comprend
rien à ce qu'il dit. Il interroge Bernard qui répond: "
Albert dit qu'il ne ment pas". Qui est le Véridique? |
||
Voir Solution
|
|
||
|
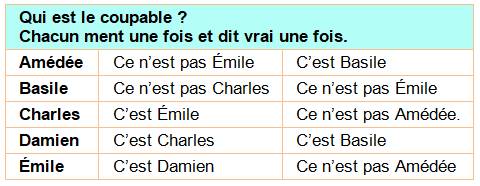
Situation Le
coupable est menteur et les deux autres disent la vérité. |
Conversation Albert: Bernard est coupable. Bernard:
Chloé est coupable. Chloé: Bernard ment. |
|
|
Énigme: Qui est le coupable? |
||
Voir Solution
|
|
||
|
Situation Albert
est menteur en début de semaine: lundi, mardi et mercredi. Bernard
est menteur en fin de semaine: jeudi, vendredi et samedi |
Corinne
entend cette conversation: Albert: tiens, hier j'ai menti! Bernard:
comme c'est drôle, moi aussi! |
|
|
Énigme Quel jour de la semaine sommes –nous, ce jour-là? |
||
Voir Solution
![]()
|
|
||
|
Situation Dans
la salle: 20 personnes. Trois
catégories: les adeptes de cinéma, ceux de musique et ceux de sport. Ils
y ceux qui disent toujours la vérité et ceux qui mentent. D'après
le sondage, combien sont menteurs? |
Sondage: quelle est votre
passion? Cocher oui ou non pour chaque rubrique:
12
cochent cinéma, 5 musique, et 8 sport. |
|
|
Solution Chacun
donne trois réponses dont une positive et deux négatives. Sauf
le menteur qui donne deux positives et une négative. Autrement-dit, le
menteur introduit une réponse positive en trop. |
Quantité
de personnes: 20 Quantité
de Oui: 12 + 5 + 8 = 25 Quantité
de Oui en trop: 25 – 20 = 5 Il
y a 5 menteurs dans l'assistance. |
|
Retour / Voir Lapins et canards
|
|
|||
|
Situation Albert
est véridique lorsqu'il est joyeux, menteur autrement. Bernard
est menteur lorsqu'il est joyeux, véridique autrement. |
Systématiquement l'un est joyeux lorsque l'autre est
triste. Énigme Comment
reconnaître Albert et Bernard à coup sûr? |
||
|
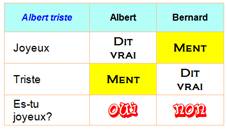
Solution Tableau
montrant la situation générale. |
|
||
|
On pose la
question: es-tu joyeux? Dans les
deux cas, Albert est celui qui répond oui et Bernard, celui qui répond non. |
|
||
|
|
|
|
"Si je demandais à votre
collègue si cette porte (il en montre une) donne la
liberté Que me dirait-il ?" Réponse du gardien et choix du prisonnier Si le gardien dit: mon collègue dirait
c'est la porte de la prison le prisonnier choisit alors la porte
désignée. Si le gardien dit: mon collègue
dirait c'est la porte de la liberté le prisonnier choisit alors l'autre porte. |
|
|
|
|
|
Rapide L'information depuis la désignation
de la porte jusqu'à l'oreille du prisonnier passe par deux cerveaux dont l'un dit la vérité
et l'autre ment. Donc, l'information qui arrivera au
prisonnier sera toujours un mensonge. Il devra
inverser la proposition qui lui est indiquée: Si la réponse est "Liberté",
c'est en fait "Prison". Il
faut choisir l'autre porte. Si la réponse est "Prison", c'est en fait "Liberté". Il faut
la choisir. Détaillée Deux cas: ou le collègue montre la porte de la
liberté, ou il montre celle de la prison. Le message passe par deux cerveaux:
le collègue puis le gardien qui est interrogé ou le collègue dit la vérité ou il ment; puis, ou le gardien dit la vérité ou il
ment. Soit quatre possibilités. Le diagramme suivant montre tous ces cas et
donne la solution.
Il dit prison, c'est la porte
liberté, il faut la prendre; Il dit liberté, c'est en fait
prison, il faut prendre l'autre porte. |
|
|
|
|||
|
Analysons les deux cas possibles et
vérifions quel est le scénario plausible. On montre l'attitude de chacun selon
l'hypothèse qu'il est Véridique ou Menteur. On ajoute une colonne centrale
pour bien indiquer ce que dit Albert selon Bernard. Scénario 1 |
|||
|
Bernard Menteur |
donc, Albert à dit |
Albert Véridique |
|
|
Albert dit qu'il ne ment pas. |
|
|
|
|
M |
Je suis le Menteur. |
V |
|
|
Scénario
incohérent. |
|||
|
Scénario 2 |
|
|
|
|
Bernard Véridique |
donc, Albert à dit |
Albert Menteur |
|
|
Albert dit qu'il ne ment pas. |
|
|
|
|
V |
Je ne mens pas Je suis le véridique. |
M qu'il est le Véridique. |
|
|
Scénario cohérent. |
|||
|
C'est Bernard le VÉRIDIQUE. |
|||
|
|
||||||||||||||||||||||||||||||||||||
|
Solution – Mise en table de vérité Exemple de lecture: Si A est
le menteur (m), alors son propos est
faux et ce n'est pas Bernard (pas B) qui est le coupable.
En observant les trois colonnes
"déclarations", seule celle ou B est le menteur est cohérente:
Albert affirme que Bernard est le menteur et les deux autres disent que ce
n'est pas Chloé, ce qui est juste. Bernard est le menteur. |
||||||||||||||||||||||||||||||||||||
|
|
|
|
Que cherchons-nous, en fait? Cette énigme est très classique. Notre but
ici est de la décortiquer pour mettre au point une méthode de résolution
systématique. Nous allons voir que cette énigme est posée
avec deux locuteurs:
Parmi
ces deux paires de jours, l'un est commun
et constitue la solution de l'énigme. Que cherchons-nous dans cette énigme? Nous
cherchons une cohérence logique dans les
propos des deux locuteurs:
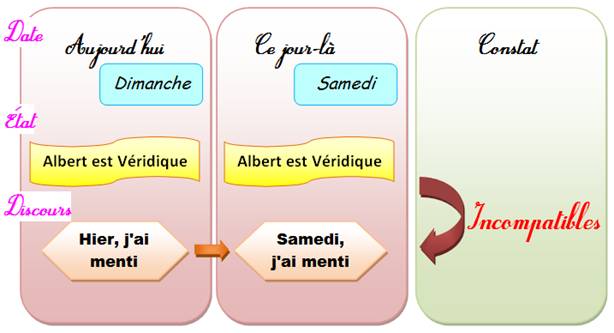
Exemple (explications à suivre sur l'illustration
ci-dessous)
Illustration
Cette situation est logiquement impossible,
nous ne sommes pas un dimanche. Examen des jours de la semaine En jaune le locuteur dit la vérité, il est
"véridique". En vert, les jours où le discours
est cohérent. Exemple de lecture:
Albert
le lundi dit qu'il a menti hier; puisqu'il est menteur le lundi, nous devons
prendre la négation de son affirmation: "hier dimanche, j'ai dit vrai". Or dimanche est un de ses jours de vérité. Son propos est logique.
Le jour cherché peut très bien être le lundi.
Parmi les deux possibilités pour Albert et
pour Bernard, seul le jeudi est un jour commun. Le jour cherché est le jeudi. |
|
Merci
à Mathias Z. pour sa pertinence à propos de cette énigme
|
|
||
|
Suppose there are two identical twin brothers, one who always lies and
the other who always tells the truth.
The interesting thing is that each brother will give the same answer
to the same question. For example, suppose you ask whether two
plus two equals four.
|
Supposez qu'il existe une paire de jumeaux dont l'un ment toujours et
l'autre dit toujours la vérité.
Il est intéressant de noter que chaque frère donnera la même réponse à
la même question. Par exemple, si vous demandez si deux plus deux égal quatre.
|
|
Extrait d'un texte de Smullyan
(par cut-the-knot.org)
|
On
pose la question: "est-ce que tu es le
véridique?" à un menteur. En
son for intérieur, le menteur ne pense pas correctement, il se croit le
véridique. Lorsqu'il va se prononcer, il va inverser la réponse et répondre :
non! je ne suis pas le véridique, je suis
le menteur. Or étant effectivement le menteur, il ne ment nullement en disant
cela, il est donc un véridique. Paradoxe?
En
général, on considère que chacun y compris le menteur est conscient de son état. En l'occurrence, le
menteur sait qu'il ment et va répondre faussement: oui,
je suis le véridique. On évite de propager le mensonge à deux
reprises: une fois dans la tête et une fois en paroles. |
|
|

Solution
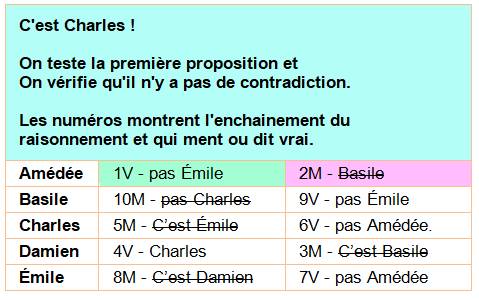
Énigme parue dans Ouest-France
avec solution le 13/03/2019
![]()
|
Voir |
|
|
|
|
|
Sites |
|
|
Livres |
|
|
Cette page |
![]()