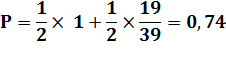|
||||||||||||||||||||||||||||||||||||||||||||||||||
![]()
|
DILEMME DU PRISONNIER Situation montrant combien
la coopération est bénéfique, mais difficile à mettre en œuvre. |
|
Deux
étudiants arrivent en retard à un examen suite à une "panne
d'oreiller". Ils se justifient auprès de l'examinateur: "nous
étions chez notre grand-mère souffrante pour la nuit. Elle habite un peu loin
et, ce matin, nous avons eu une crevaison, désolé monsieur".
Compréhensif, l'examinateur les place chacun à un bout de la salle, et il
leur donne la feuille d'examen accompagnée d'une question liminaire,
éliminatoire en cas de réponse erronée: quelle roue pour la crevaison? |
Voir Pensées & humour
|
|
||
|
Il existe de nombreuses énigmes octroyant la liberté sous
conditions. En voici une avant d'entreprendre le célèbre dilemme du prisonnier. Problème Le prisonnier doit sa chance
de liberté à une énigme. Il dispose de 20 balles blanches et 20 balles noires
à placer à sa convenance dans les deux urnes. Les deux urnes sont posées au
hasard sur la table. Si, les yeux bandés, il tire une boule blanche, il est sauvé. Quelle est sa tactique pour
maximiser ses chances. |
Solution 1) S'il met les 20 noires
dans une urne et les 20 blanches dans l'autre, sa probabilité de liberté est d'une
chance sur deux. 2) S'il met 10 noires et 10
blanches dans chaque urne et même chose dans l'autre. La probabilité de
liberté reste 50%. 3) S'il met une seule balle
blanche dans une urne et le reste dans l'autre, la probabilité de liberté se
calcule de la façon suivante:
Avec cette tactique, il a
pratiquement 3 chances sur 4 de s'en sortir. |
|
|
|
|
|
Énoncé
La
police leur fait la proposition suivante:
Les
interrogations se font avec chacun des prisonniers, séparément. L'un ne
connait pas la réponse de l'autre. Mise
en tableau
|
|
|
|
|
|
En
effet
Ils
prennent quatre ans chacun. Résumé Hypothèse: Albert, le coupable, se déclare innocent
|
|
|
|
|||||||||||||
|
Résumé Hypothèse: Albert, le coupable, ne parle pas
|
|||||||||||||
|
|
|
|
Résumé
en termes de peines encourues et d'injustice Si Albert, le coupable, joue l'innocent en ne disant rien,
il encoure 2 ans ou 5 ans, soit –3 et 0 par rapport à la peine méritée. Un
total de –3 ans dans ce cas. Dans l'autre cas où il se dit innocent, il
observe une remise de peine pour un total de 6 ans (– 5 et – 1, non cumulables, certes!). On comprend qu'Albert
choisisse cette attitude (innocent), a priori.
Par contre, Bernard osera-t-il parier sur le cas où
Albert ne parlera pas, là où le bilan de l'injustice pour lui ne serait que
de 2 ans; alors que dans l'autre cas, il écoperait d'un lourd bilan: 9 ans. |
|
Commentaires
|
Je
m’amuse à penser qu’il pourrait y avoir une tactique N°3: le double
acquittement: Albert dénonce Bernard comme innocent et Bernard dénonce Albert
comme innocent lui aussi. Résultat
: un double acquittement possible ? …
ou au pire un tirage au sort à pile ou face; …
dans tous les cas le choix revient à la police et non plus aux prisonniers
potentiels. Le
seul vrai problème c’est que probablement aucun des deux prisonniers ne peut
avoir confiance l’un dans l’autre… Conclusion
: le risque serait probablement de deux ans pour chacun ou de cinq pour un
seul des 2 (soit un risque de 2 ou 5 ans à pile ou face) Une
dernière remarque : on part du postulat qu’il y a un coupable, et qu’il ne se
risquera pas à se dénoncer comme tel … Vincent M. |
![]()
|
Suite |
|
|
Voir |
|
|
Cette page |
![]()