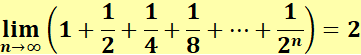|
|||||||||||||||||||||||||||||
![]()
|
ACHILLE & LA TORTUE Achille ne peut
jamais atteindre la tortue! Il faut avoir
assimilé les concepts de l'infini,
du zéro
et, en résumé, des limites pour résoudre ce paradoxe. |
|
|
||
|
Atterrissage |
Principe d'encadrement par dichotomie. Comme l'avion qui
atterrit, la courbe asymptotique se rapproche sans cesse d'une ligne droite.
À mesure que cette courbe et la ligne convergent, la distance qui les sépare
est continuellement divisée de moitié.
Mais quel que soit le point atteint, il restera toujours une moitié à faire,
et ceci, même à l'infini.
Paradoxe de la ligne asymptotique ou Paradoxe d'Achille et la
tortue. |
|
|
Antinomies de Zénon d'Élée
Grec, vers 500 avant J.-C. |
||
|
La flèche n'atteint jamais sa cible |
Chaque fois que la flèche a parcouru la moitié de son
chemin, il lui en reste une autre moitié à parcourir. |
|
|
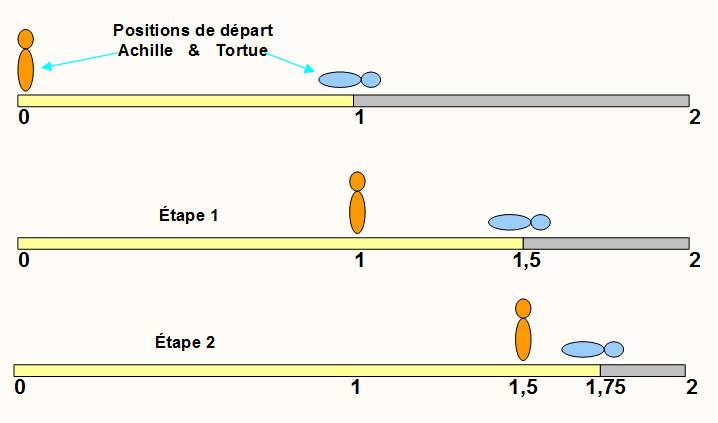
Achille ne rattrape jamais la tortue |
La tortue est
partie en avance (eh, oui!). Elle est déjà loin lorsqu'Achille se met à courir. Au moment où Achille atteint le point où elle se
trouvait, la tortue a fait du chemin. Chaque fois qu'Achille passe par le point où se
trouvait la tortue celle-ci, pendant ce temps, progresse … |
|
Voir Nombre
0,5 / Zénon d'Élée
|
|
|
|
Illustration
|
|
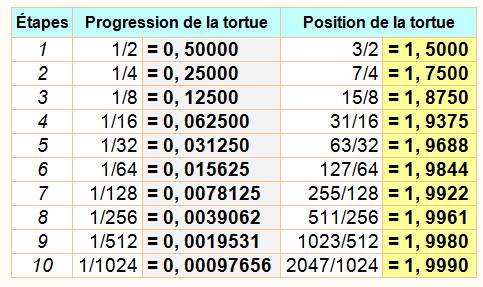
Voir Somme des
inverses des puissances de 2
|
|
|
|
Les
Grecs n'avaient pas d'explication à ce paradoxe. |
|
|
Chaque terme est comme un voyage dont la destination serait zéro |
Zéro - La biographie d'une idée dangereuse
– Charles SEIFE
|
|
|
|
Quel que soit l'écart
que l'on décide entre Achille et la tortue, il existe une étape pour laquelle
Achille et la tortue sont assez proches pour tenir dans cet écart.
Voir Nombre 2
|
|
![]()
|
Voir |
|
|
|
|
|
Site |
|
|
Cette page |
![]()