|
|
Définitions |
Voir Redondance / Multiensemble |
|
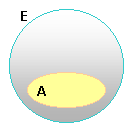
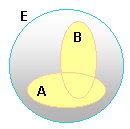
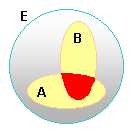
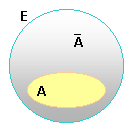
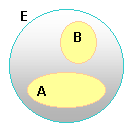
Ensemble ou classe |
|
|
Oups! |
Mais des relations et des règles d'emplois et … des paradoxes, parfois. |
![]()
|
Exemples d'ensembles |
|
|
Notations |
|
![]()
|
Caractérisation |
Un ensemble peut être caractérisé par l'une des
deux manières suivantes:
|
|
Types |
Un ensemble peut-être:
|
![]()
|
Intérêt |
Trouver des caractéristiques communes à des
groupes d'objets et, de ce fait, traiter globalement la collection
(l'ensemble) au nom de tous les objets.
|
|
Théorie |
La théorie des ensembles
traite de toutes ces propriétés:
|
![]()
|
De la définition originelle formulée par Cantor résultait
des paradoxes. Célèbre mise en évidence par Russel dans le paradoxe
qui porte son nom:
|
||
|
Mathématiciens |
Mathématiciens associés à la théorie des
ensembles
|
![]()
|
Anglais |
Set A well-defined collection of objects. It may be possible to define a set by listing the elements or as
consisting of all elements that satisfy some property. Kamke's definition (Theory of Sets – 1950) By a set we are to understand, according to G. Cantor, "a collection into a whole, of definite, well-distinguished objects (called the
elements) of our perception or of our thought…" For a set, the order
of succession of its elements shall not matter… Furthermore, the same element
shall not be allowed to appear more than once.
The number complex 1, 2, 1, 2, 3
consequently, becomes a set only after deleting the repeated elements. A multiset is a collection of
objects (called elements) in which elements may occur more than once. >>> |
|
Suite |
|
![]()
![]()
|
||||||||||||
Suite en Cardinal
![]()
|
||||||||||||||||||
Suite en Logique de
Boole
![]()
|
|||||||||||||
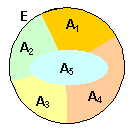
Suite en Partition
![]()
|
|||||||||||||||
![]()
![]()
![]()