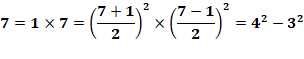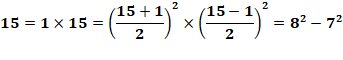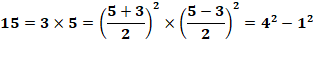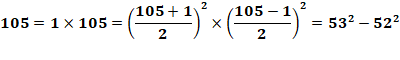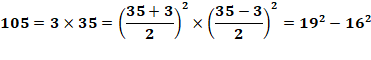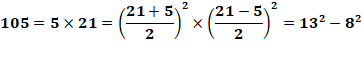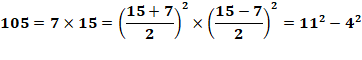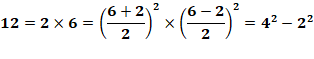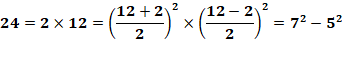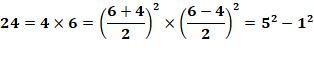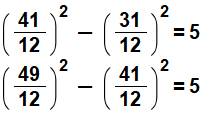|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
![]()
|
DIFFÉRENCE des carrés de deux nombres
Propriété TOUT
nombre est égal à une différence de carrés, au moins. Voir la suite des propriétés |
Voir Nombres
Impairs et différence de carrés
|
|
||
|
Observations On
cherche les nombres égaux à une différence de deux nombres au carré, comme 12
= 4² – 2². Avec les
nombres pairs,
Avec les
nombres impairs,
|
Nombres
pairs & Nombres impairs
|
|
Voir Pair et
impair
Records de quantité de différences de carrés jusqu'à 1000
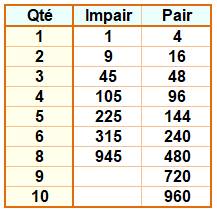
Voir Nombre 105 comme exemple
|
|
||
|
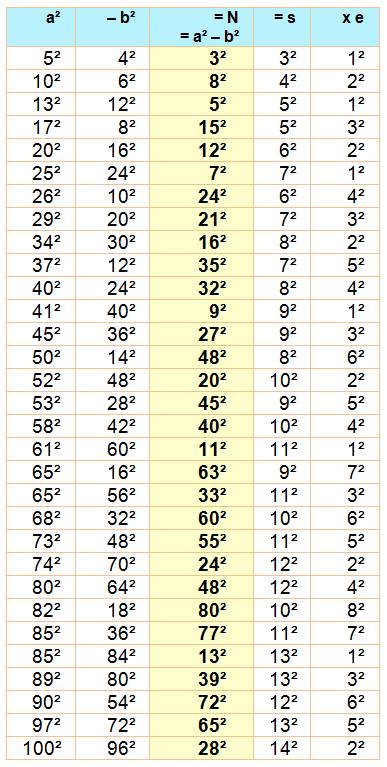
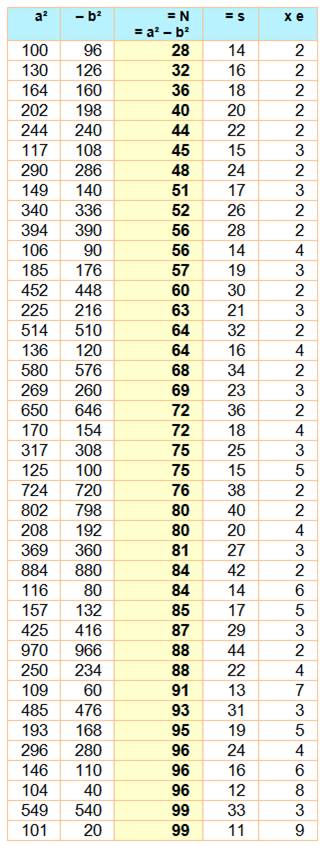
Explications Avec l'identité
remarquable, on déduit immédiatement que:
les nombres portés au carré ont s pour somme et e pour différence
(écart) |
N = a² – b² = (a – b) (a +
b) = e . s Si un nombre (N) est différence de deux carrés, il est le produit de la
somme (s) de ces deux nombres et de leur différence (e). |
|
|
Relations entre ces quatre nombres
|
|
|
|
Conditions Les
fractions exprimant a et b ne sont des nombres
entiers que si (s +e) est pair; ce qui impose:
|
Exemples 7 = 1 x 7 tous deux impairs a = 8/2 = 4 et
b = 6/2 = 3 7 = 4² – 3² = 16 – 9 8 = 2 x 4 tous deux pairs a = 6/2 = 3 et
b = 2/2 = 1 8 = 3² – 1² = 9 – 1 |
|
Voir Recherche sur la
somme et la différence des facteurs d'un nombre
|
|
||
|
Méthode
|
Exemple
Avec t = 4 diviseurs, on forme Q = t/2)= 2 couples dont le produit des membres est N. |
|
|
Quantité Soit t
(en fait tau) est la quantité
de diviseurs, il existe en général t/2 couples tels que leur produit est
égal à N. Deux cas
critiques cependant:
|
La quantité de présentations est égale à la quantité de couples de
diviseurs dont les valeurs sont de même parité. Cas de parités différentes 10 et ses diviseurs {1, 2, 5,
10} Les couples (1, 10) et (2,
5) ne sont pas de même parité. Aucune différence
de carré possible. Cas d'une quantité impaire de diviseurs 16 et ses diviseurs {1, 2, 4,
8, 16} Seul le couple (2, 8) crée une différence de carrés. |
|
|
|
||
|
Nombres impairs premiers À la
différence des autres nombres, les nombres
premiers (P) offrent un seul couple (1, P) et donc qu'une seule possibilité
de différence de carrés. Elle
existe toujours, car le couple (1, P) est bien de même parité impaire. |
P = 1 x P avec seulement deux diviseurs Exemple Un nombre impair premier est une seule fois différence de deux carrés consécutifs. |
|
|
Nombres impairs composés Avec au
moins deux diviseurs de plus que pour les nombres premiers, ils offrent au
moins un couple de plus. Ce couple
est éligible, car tous les diviseurs d'un nombre impair sont impairs. La
quantité de présentation (Q) est égale à la moitié de la quantité des
diviseurs. Pour les
nombres dont la quantité de diviseurs est impaires: Q = entier(t/2). |
Exemple
Propriété Si t est la quantité de diviseurs d'un nombre impair composé, alors il
est Q = t/2 fois différence de deux carrés, dont une fois de nombres
consécutifs. Exemple de calcul de quantité Diviseurs de 105 {1, 3, 5, 7, 15, 21, 35, 105} Quantité de présentations: Q = t/2 = 8/2 = 4
|
|
|
|
||
|
Nombres pairs Si N est
pair, alors e et s sont tous deux pairs, donc N est divisible par 4 Les
nombres pairs non divisibles pas 4 (N = 4k + 2) sont exclus. Le
premier couple (1, N) de diviseurs, avec N pair, n'est pas éligible. Tous les
couples avec un diviseur impair sont disqualifiés. Le
décompte n'est pas chose facile, car la parité des diviseurs est hétérogène. |
N = a² – b² = (a – b) (a + b) = e . s Exemples de calcul de quantité Diviseurs de 12 {1, 2, 3, 4, 6, 12} avec t = 6 et Q = 1 Couples (1, 12), (2, 6) (3, 4).Seul (2,6) est de même parité.
Diviseurs de 24 {1, 2, 3, 4, 6, 8, 12, 24} avec t = 8 et Q = 2
Diviseurs de 48 {1, 2, 3, 4, 6, 8, 12, 16, 24, 48} avec t = 10 et Q =3
Un nombre N composé pair-impair (divisible par 4) est toujours
différence de deux carrés non consécutifs. Aucune présentation avec deux nombres consécutifs. La quantité de
présentations est au plus égale à la moitié de la quantité des diviseurs. |
|
Merci à Anthony Fernandes pour sa lecture attentive
|
Propriétés Tous les nombres sont différences de
deux carrés sauf ceux en 4k + 2 et les nombres: 1, 2 et 4. Tout nombre impair est différence de
carrés de nombres consécutifs. S'il est premier, c'est la seule présentation;
sinon, il en possède au moins une autre. Note:
le calcul de la quantité de présentations doit tenir compte de la parité de N
et aussi du fait que N est une puissance pure ou non. Construction Un couple de diviseurs (s et e, avec
s . e = N), de même parité, produit une différence de carrés N = a² – b²
telle que:
|
Voir Illustration
/ Pour aller plus loin
Merci à
Bruno Payet pour toutes ses suggestions
![]()
Balade sur le sujet: différences de deux
carrés
|
|
|
|
Somme
des premiers impairs consécutifs égale différence de leur carré 3 = 1 + 2 = 2² – 1² 5 = 2 + 3 = 3² – 2² 7 = 3 + 4 = 4² – 3² 9 = 4 + 5 = 5² – 4² … Vrai pour tout
nombre impair, et notamment lorsqu'ils sont carrés,
engendrant alors et systématiquement un triplet
de Pythagore. 9² = 81 = 2 x 40 + 1 = 40 + 41 = 41² – 40² Suite Table de 1 à 100 Voir Nombres
consécutifs |
|
|
|
||||||||||
|
La somme de deux nombres consécutifs,
un nombre
impair, est égale à la différence de leur carré. Démonstration
|
||||||||||
|
Démonstration
géométrique Soit un nombre impair quelconque
(13). On le plie en deux: 13 = 6 + 7
(cases bleues). On remplit l'espace dans l'équerre
(jaune) On lit les relations: grand carré –
carré jaune = zone bleue: 7² – 6² = 13 |
|
|||||||||
|
|
|||||||||||||||||||
|
Liste
pour n jusqu'à 20 n n-1 Somme n² (n-1)² Différence 1 0 1 1 0 1 2 1 3 4 1 3 3 2 5 9 4 5 4 3 7 16 9 7 5 4 9 25 16 9 6 5 11 36 25 11 7 6 13 49 36 13 8 7 15 64 49 15 9 8 17 81 64 17 10 9 19 100 81 19 11 10 21 121 100 21 12 11 23 144 121 23 13 12 25 169 144 25 14 13 27 196 169 27 15 14 29 225 196 29 16 15 31 256 225 31 17 16 33 289 256 33 18 17 35 324 289 35 19 18 37 361 324 37 20 19 39 400 361 39 En rouge: trois carrés, triplets
de Pythagore Autres
exemples
Beau moyen de faire
se répéter les chiffes |
|||||||||||||||||||
|
|
|||||||||||||||||
|
Généralisation
Conséquence
Exemples
|
|||||||||||||||||
Voir Calcul des nombres avec somme et produit
connus / Nombre
111
Voir Différence de carrés = produit de cubes
|
|
|||
|
Tableau
des nombres congruum (en rouge) jusqu'à r = 10 000.
|
|||
Voir Historique
![]()
|
Retour |
|
|
Suite |
|
|
Voir |
|
|
DicoNombre |
|
|
Cette page |
http://villemin.gerard.free.fr/Wwwgvmm/Addition/P100a500/Difcarth.htm |
![]()