|
||||||||||||||||||||||||||||||||||||||||
![]()
Vision générale: Nombre en ak + h premiers ou non
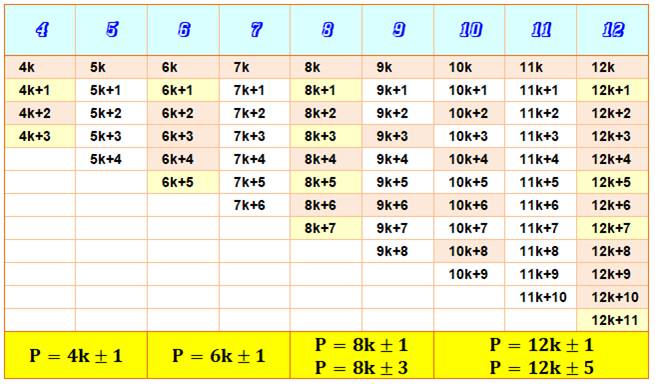
Tous les nombres
premiers sont en 4k + 1 ou 4 k – 1 (idem que 4k + 3)
ou de la forme 6k + 1 ou
6k – 1, etc. (se prolonge, même au-delà de 12)
Cependant, tous les
nombres de ces formes ne sont pas toujours premiers.
Explications ci-dessous
![]()
|
Nombres premiers P = 4n ± 1
Comme on le fait avec les nombres pairs et impairs En effet: Pair = 2n & Impair = 2n + 1
|
|
|
|||||||||
|
Condition
nécessaire, mais pas suffisante
|
Voir Tableau |
||||||||
|
Cette forme est assez triviale puisqu'elle
indique que seuls les nombres impairs (hormis 2) sont premiers. Un évidence! |
|
||||||||
|
|
||
|
Prenons toutes les possibilités de division par 4 |
Reste 0, 1, 2
ou 3. |
|
|
Reste 0 => nombre en 4k |
=> composé, divisible par 4 |
|
|
4k + 1 |
=> premier possible |
|
|
4k + 2 |
=> composé, divisible par 2 |
|
|
4k + 3 = 4(k + 1) - 1 = 4k' – 1 |
=> premier possible |
|
|
Un nombre premier ne peut être que de la forme |
4n ± 1 |
|
|
|
||
|
|
Voir Caractérisation et
liste de ces nombres premiers dits de Pythagore |
|
|
|
Exemples 2² x
5 = 20 = 4² +
2² 3² x
5 = 45 = 6² +
3² 4² x 13 = 208 = 12² + 8² 5² x 13 = 325 = 15² + 10² |
|
|
ILLUSTRATION en cercle |
|
|
|
|
Voir suite en Cercles
et croix en 4, 6 12 …
|
Répartition selon les
facteurs |
|
|
|
Tout
nombre est décomposable en produit de facteurs (diviseurs premiers). Combien
de ces facteurs sont de la forme 4k – 1 et combien de la forme 4k + 1 ? |
Facteurs de 21 : 1, 3, 7, 21 1 = 4 x 0 + 1 3 = 4 x 1 – 1 7 = 4 x 2 – 1 21 = 4 x 5 + 1 Deux facteurs en MOINS et deux facteurs en PLUS. On note: [21, 2, 2] |
|
|
Liste selon MOINS, Égal ou PLUS Moins, 6, [[27, 2, 1], [42, 2, 1], [63, 3, 1], [66, 2, 1], [84, 2, 1],
[99, 3, 1]] Egal, 51, [[3, 1, 1], [6, 1, 1], [7, 1, 1], [11, 1, 1], [12, 1, 1],
[14, 1, 1], [15, 2, 2], [18, 1, 1], [19, 1, 1], [21,
2, 2], [22, 1, 1], [23, 1, 1], [24, 1, 1], [28, 1, 1], [31, 1, 1],
[33, 2, 2], [35, 2, 2], [36, 1, 1], [38, 1, 1], [39, 2, 2], [43, 1, 1], [44,
1, 1], [46, 1, 1], [47, 1, 1], [48, 1, 1], [51, 2, 2], [54, 1, 1], [55, 2,
2], [56, 1, 1], [57, 2, 2], [59, 1, 1], [62, 1, 1], [67, 1, 1], [69, 2, 2],
[71, 1, 1], [72, 1, 1], [75, 2, 2], [76, 1, 1], [77, 2, 2], [79, 1, 1], [83,
1, 1], [86, 1, 1], [87, 2, 2], [88, 1, 1], [91, 2, 2], [92, 1, 1], [93, 2,
2], [94, 1, 1], [95, 2, 2], [96, 1, 1], [98, 1, 1]] Plus, 43, [[1, 0, 1], [2, 0, 1], [4, 0, 1], [5, 0, 2], [8, 0, 1], [9,
1, 2], [10, 0, 2], [13, 0, 2], [16, 0, 1], [17, 0, 2], [20, 0, 2], [25, 0,
3], [26, 0, 2], [29, 0, 2], [30, 1, 2], [32, 0, 1], [34, 0, 2], [37, 0, 2],
[40, 0, 2], [41, 0, 2], [45, 1, 3], [49, 1, 2], [50, 0, 2], [52, 0, 2], [53,
0, 2], [58, 0, 2], [60, 1, 2], [61, 0, 2], [64, 0, 1], [65, 0, 4], [68, 0,
2], [70, 1, 2], [73, 0, 2], [74, 0, 2], [78, 1, 2], [80, 0, 2], [81, 1, 2],
[82, 0, 2], [85, 0, 4], [89, 0, 2], [90, 1, 2], [97, 0, 2], [100, 0, 2] |
||
|
|
||
|
Répartition selon les
diviseurs |
|
||||||||||||||||||||||||||||||||||||||
|
Combien
de ces diviseurs sont de la forme 4k – 1 et combien de la forme 4k + 1 ? |
Diviseurs de 27 : 1, 3, 9, 27 1 = 4 x 0 + 1 3 = 4 x 1 – 1 9 = 4 x 2 +1 27 = 4 x 7 – 1 Deux diviseurs en MOINS et deux diviseurs en PLUS. On note: [27, 2, 2] |
||||||||||||||||||||||||||||||||||||||
|
Liste selon MOINS, Égal ou PLUS Moins, 0, [] Egal, 57, [[3, 1, 1], [6, 1, 1], [7, 1, 1], [11, 1, 1], [12, 1, 1], [14,
1, 1], [15, 2, 2], [19, 1, 1], [21, 2, 2], [22, 1, 1], [23, 1, 1], [24, 1,
1], [27, 2, 2], [28, 1, 1], [30, 2, 2],
[31, 1, 1], [33, 2, 2], [35, 2, 2], [38, 1, 1], [39, 2, 2], [42, 2, 2], [43,
1, 1], [44, 1, 1], [46, 1, 1], [47, 1, 1], [48, 1, 1], [51, 2, 2], [54, 2,
2], [55, 2, 2], [56, 1, 1], [57, 2, 2], [59, 1, 1], [60, 2, 2], [62, 1, 1],
[63, 3, 3], [66, 2, 2], [67, 1, 1], [69, 2, 2], [70, 2, 2], [71, 1, 1], [75,
3, 3], [76, 1, 1], [77, 2, 2], [78, 2, 2], [79, 1, 1], [83, 1, 1], [84, 2,
2], [86, 1, 1], [87, 2, 2], [88, 1, 1], [91, 2, 2], [92, 1, 1], [93, 2, 2],
[94, 1, 1], [95, 2, 2], [96, 1, 1], [99, 3, 3]] Plus, 43, [[1, 0, 1], [2, 0, 1], [4, 0, 1], [5, 0, 2], [8, 0, 1], [9,
1, 2], [10, 0, 2], [13, 0, 2], [16, 0, 1], [17, 0, 2], [18, 1, 2], [20, 0,
2], [25, 0, 3], [26, 0, 2], [29, 0, 2], [32, 0, 1], [34, 0, 2], [36, 1, 2],
[37, 0, 2], [40, 0, 2], [41, 0, 2], [45, 2, 4], [49, 1, 2], [50, 0, 3], [52,
0, 2], [53, 0, 2], [58, 0, 2], [61, 0, 2], [64, 0, 1], [65, 0, 4], [68, 0,
2], [72, 1, 2], [73, 0, 2], [74, 0, 2], [80, 0, 2], [81, 2, 3], [82, 0, 2],
[85, 0, 4], [89, 0, 2], [90, 2, 4], [97, 0, 2], [98, 1, 2], [100, 0, 3]] |
|||||||||||||||||||||||||||||||||||||||
|
Théorème |
Un théorème de Legendre dit que: si M est la quantité des diviseurs en
4k – 1 et P celle en 4k + 1, la quantité de représentations de n comme somme
de deux carrés est égale à 4(P – M). Alors, P ≥
M pour tout nombre. Il n'existe aucun nombre ayant moins de diviseurs
en 4k – 1 qu'en 4k + 1. |
||||||||||||||||||||||||||||||||||||||
|
Record de quantité Ces nombres sont également P/2 fois somme
de deux carrés. |
|
||||||||||||||||||||||||||||||||||||||
![]()
|
Voir |
|
|
Aussi |
|
|
|
|
|
Cette page |
![]()


