|
||||||||||||||||||||||||||||||||||||||||||||
![]()
|
Quelques IDENTITÉS importantes |
|
(a + b)2 + (a – b)2 (a + b)2 – (a – b)2 (a + b)3 + (a – b)3 (a + b)3 – (a – b)3 (a + b)4 + (a – b)4 (a + b)4 – (a – b)4 |
= = = = = = |
2(a² + b²) 4 ab 2a( a² + 3b²) 2b(3a² + b²) 2(a4 + 6a²b² + b4) 8ab (a² + b²) |
|
||
|
(a² + b²) (A² + B²) |
= |
(aA – bB)² + (aB + bA)² |
|
||
|
(a² + b²) (A² + B²) |
|
(aB + bA)² |
|
||
|
(a² + kb²) (A² + kB²) |
= |
(aA – bBk)² + k(aB + bA)² |
|||
|
(a² + b² + c²) (A² + B² + C²) |
= |
(aA + bB + cC)² + (aB – Ab)² + (bC – Bc)² + (cA – Ca)² |
|||
|
(a2
+ b2 + c2 + d2)² |
= |
(a2 + b2 – c2 – d2)² + (2ac + 2bd)² + (2ad – 2bc)² |
|
||
|
(a
– c) (b – a) (c – b) |
= |
a²(b – c) + b²(c – a) + c²(a – b) |
|||
|
(a2+b2+c2+d2)(A2+B2+C2+D2) |
= |
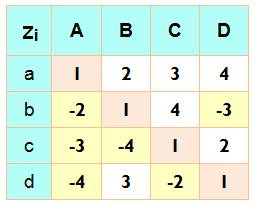
z12 + z22 + z32
+ z42 avec z1 = aA + bB + cC + dD z2 = aB – bA + cD – dC z3 = aC – cA – bD + dB z4 = aD – dA + bC – cB |
|
|
|
Exemples |
(1²+2²+3²+4²)(5²+6²+7²+8²) = 25 x 174 = 63² + (16)² +5² + (-10)² = 4 350 (1²+3²+5²+7²)(2²+4²+6²+8²) = 84 x
120 = 100² + (-4)² + 0² + (-8)² = 10 080 |
|||
|
Généralisation Le produit
de nombres, chacun somme de quatre carrés, est somme de quatre carrés. |
|
|||
Voir Théorème des quatre carrés de Lagrange
|
(a
+ b + c)2 + (a – b – c)2 |
= |
2(a² + b² + c²) + 4bc |
|||
|
|
|
||||
|
a3
+ a2 + a + 1 |
= |
(a + 1) (a² + 1) |
|
||
|
a4
+ a2 + 1 |
= |
(a² + a + 1) (a² – a + 1) |
|
||
|
a4
+ 4b4 |
= = |
{(a + b)² + b²} {(a – b)² + b²} (a² + 2ab + 2b²) (a² – 2ab + 2b²) |
Identité de
Sophie
Germain |
||
Identité
du triple et du quadruple quad
|
Si
a + b = c |
(a²
+ b² + c²)2 = 2(a4 + b4 + c4) |
|
Si
a + b = s Et
c + d = s |
{ (a² + b²
+ c² + d²) – 2(a4 + b4 + c4 + d4)
}2 = 64 a²b²c²d² |
Voir Triple quad
Identité des quatre carrés d'Euler
|
Euler Four Square Identity can be verified by expanding out the parentheses in
both sides. Its deeper meaning becomes clear only after one can become
acquainted with the algebraic objects called "quaternions" – Oleg A.
Ivanov |
|
Cette relation:
Peut être transposée en (avec x
|
|
Quelques exemples:
Nombres atteint par cette relation pour x et n
jusqu'à 10 7,
13, 15, 21, 31, 40, 43, 57, 63, 73, 85, 91, 111, 121, 127, 156, 255, 259,
341, 364, 400, 511, 585, 781, 820, 1023, 1093, 1111, 1365, 1555, 2801, 3280,
3906, 4681, 5461, 7381, 9331, 9841, 11111, 19531, 19608, 21845, 29524, 37449,
55987, 66430, 87381, 97656, 111111, 137257, 299593, 335923, 349525, 488281,
597871, 960800, 1111111, 2015539, 2396745, 2441406, 5380840, 6725601,
11111111, 12093235, 19173961, 47079208, 48427561, 111111111, 153391689,
435848050, 1111111111 … |
|
|
= |
|
|
|
|
= |
|
|
|
1 + x+ x2 + x3 + … = 1 / (1 –
x) |
|
||
|
1 |
= |
a.u + b.v |
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Identité
de Brahmagupta
Suite
sur ce genre d' Identités Vérification de la
formule
Conséquence
Formulation (a² + b²) (c² + d²)
= (ad + bc)² + (ac - bd)² m = a² + b² n = c² + d² m.n = u² + v²
Liste des premiers
nombres ayant cette propriété
Liste 4 10 16 20 25 26
34 36 40 50 52 58
64 65 68
74 80 82
85 90 100 104 106
116 125 130
136 144 145
146 160 164
170 180 185
194 200 202 205
208 … |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Voir Théorie
de la somme de deux carrés
Deux identités remarquables de Ramanujan
|
|
Voir Développements
|
|
||
|
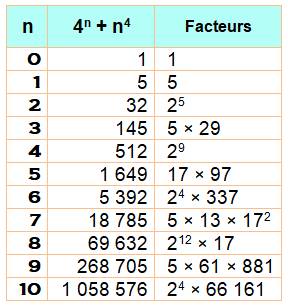
Montrez que cette expression est composée, sauf pour n = 1. |
|
|
|
E est un
carré tronqué: |
|
|
|
Premières vérifications Valeur
pour n = 1 |
4 + 1 = 5 premier |
|
|
Valeur
pour n = 2 |
42 + 24 = 16 + 16 =
32 composé |
|
|
Valeur
pour n = 3 |
43 + 34 = 64 + 81 =
145 composé |
|
|
Valeur
pour n = 2k |
42k + (2k)4 = 2K
composé |
|
|
Valeurs impaires de n Valeur
pour n = 2k – 1 ou n + 1 = 2k. Le deuxième terme devient un carré et propice à
l'application d'une identité remarquable. |
|
|
|
Cette expression
n'est première que si le plus petit facteur est égal à 1, ou composé si
supérieur à 1. Compte tenu des vérifications pour n jusqu'à
3, il suffit de vérifier au-delà. Conclusion: aucun des deux
facteurs ne peut égaler 1, l'expression représente toujours n nombre composé. |
n = 3 => 23
+ 32 = 8+9 = 17 & 3x22 = 12 Inégalité vérifiée
pour 3 et au-delà. Plus formellement (n>3): 2n + n2 > 2n
+ 1
= 22k – 1 + 1 = 2k .2k-1 +1 |
|
|
Vérification jusqu'à n = 10 Anglais All values (but 1)
of n^4 + 4^n for the positive integer
n are not prime. |
|
|
|
Expressions semblables (test pour n jusqu'à 100) |
Première pour n = 1, 3, 9, 15, 31, 33
Première pour n = 2, 56
Première pour n = 24 |
|
Voir Identités
remarquables du quatrième degré / Même démonstration
![]()
|
Suite |
|
|
Voir |
|
|
Site |
|
|
Cette page |
http://villemin.gerard.free.fr/Wwwgvmm/Identite/IdentSpe.htm |
![]()
Pour
ces liens voir
>>>