|
Édition du: 29/12/2020 |
|
INDEX |
Tables – FRACTIONS |
|
|
Table des périodes des fractions Table donnant le
développement décimal des fractions avec un nombre
premier pour dénominateur. Nombres périodiques.
Les nombres
têtus ou premier longs sont ceux dont la période est de longueur maximale
(p = n – 1). |
||
|
|
Sommaire de cette page >>>
Période du développement des fractions >>>
Développement décimal des fractions |
Débutants Glossaire |
Vocabulaire
|
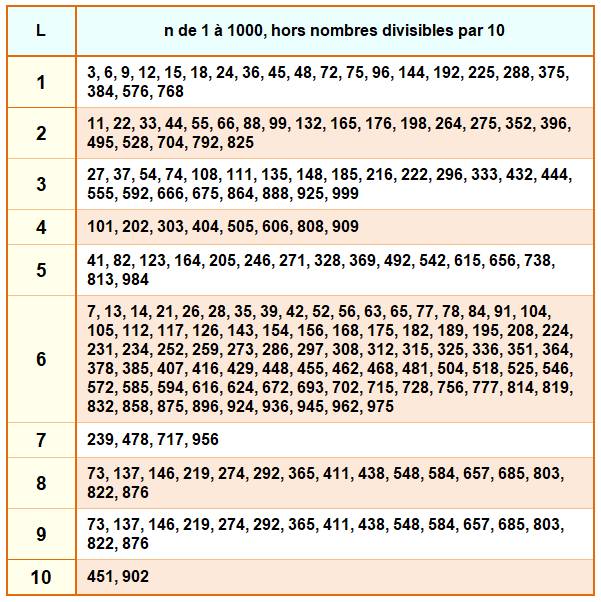
Table de 200
valeurs donnant la période du développement des fractions avec un nombre premier
pour dénominateur. Exemple 1/7 = 0, 142857
142857 … La période
142857 comporte six chiffres. Soit dans la table: [7, 6] Nombre
premier long Le nombre
premier 17, noté [17,
16] engendre une longueur maximale de 16 chiffres dont on trouvera la valeur
dans la table ci-dessous. |
[2, 0],
[3, 1], [5, 0], [7, 6],
[11, 2], [13, 6], [17,
16], [19, 18], [23, 22], [29, 28], [31, 15], [37, 3], [41, 5], [43,
21], [47, 46], [53, 13], [59, 58], [61, 60], [67, 33], [71, 35], [73, 8],
[79, 13], [83, 41], [89, 44], [97, 96], [101, 4], [103, 34], [107, 53], [109,
108], [113, 112], [127, 42], [131, 130], [137, 8], [139, 46], [149, 148],
[151, 75], [157, 78], [163, 81], [167, 166], [173, 43], [179, 178], [181,
180], [191, 95], [193, 192], [197, 98], [199, 99], [211, 30], [223, 222],
[227, 113], [229, 228], [233, 232], [239, 7], [241, 30], [251, 50], [257, 256],
[263, 262], [269, 268], [271, 5], [277, 69], [281, 28], [283, 141], [293,
146], [307, 153], [311, 155], [313, 312], [317, 79], [331, 110], [337, 336],
[347, 173], [349, 116], [353, 32], [359, 179], [367, 366], [373, 186], [379,
378], [383, 382], [389, 388], [397, 99], [401, 200], [409, 204], [419, 418],
[421, 140], [431, 215], [433, 432], [439, 219], [443, 221], [449, 32], [457,
152], [461, 460], [463, 154], [467, 233], [479, 239], [487, 486], [491, 490],
[499, 498], [503, 502], [509, 508], [521, 52], [523, 261], [541, 540], [547,
91], [557, 278], [563, 281], [569, 284], [571, 570], [577, 576], [587, 293],
[593, 592], [599, 299], [601, 300], [607, 202], [613, 51], [617, 88], [619,
618], [631, 315], [641, 32], [643, 107], [647, 646], [653, 326], [659, 658],
[661, 220], [673, 224], [677, 338], [683, 341], [691, 230], [701, 700], [709,
708], [719, 359], [727, 726], [733, 61], [739, 246], [743, 742], [751, 125],
[757, 27], [761, 380], [769, 192], [773, 193], [787, 393], [797, 199], [809,
202], [811, 810], [821, 820], [823, 822], [827, 413], [829, 276], [839, 419],
[853, 213], [857, 856], [859, 26], [863, 862], [877, 438], [881, 440], [883,
441], [887, 886], [907, 151], [911, 455], [919, 459], [929, 464], [937, 936],
[941, 940], [947, 473], [953, 952], [967, 322], [971, 970], [977, 976], [983,
982], [991, 495], [997, 166], [1009, 252], [1013, 253], [1019, 1018], [1021,
1020], [1031, 103], [1033, 1032], [1039, 519], [1049, 524], [1051, 1050],
[1061, 212], [1063, 1062], [1069, 1068], [1087, 1086], [1091, 1090], [1093,
273], [1097, 1096], [1103, 1102], [1109, 1108], [1117, 558], [1123, 561],
[1129, 564], [1151, 575], [1153, 1152], [1163, 581], [1171, 1170], [1181,
1180], [1187, 593], [1193, 1192], [1201, 200], [1213, 202], [1217, 1216],
[1223, 1222]. |
||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Sur les 200
valeurs tabulées, 77 nombres produisent des périodes maximales. Anglais: Full reptend
prime, maximal period prime, golden prime or long prime |
7, 17,
19, 23, 29, 47, 59, 61, 97, 109, 113, 131, 149, 167, 179, 181, 193, 223, 229,
233, 257, 263, 269, 313, 337, 367, 379, 383, 389, 419, 433, 461, 487, 491,
499, 503, 509, 541, 571, 577, 593, 619, 647, 659, 701, 709, 727, 743, 811,
821, 823, 857, 863, 887, 937, 941, 953, 971, 977, 983, 1019, 1021, 1033,
1051, 1063, 1069, 1087, 1091, 1097, 1103, 1109, 1153, 1171, 1181, 1193, 1217,
1223. |
||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Toutes les
fractions avec un nombre premiers p présentent les mêmes suites de nombres Quantité
de suites périodiques Quels sont les plus petits
nombres premiers p avec k suites de nombres représentant toutes les fractions
en n/p ? Quels sont les plus petits nombres premiers périodiques d'ordre k ? Exemple Avec p = 3, on a 1/3 = 0,333… et 2/3 = 0,666… Avec = = 103, Relation l x q = p – 1 Aucun nombre de
quantité de période l = 13, 15 ou 16 jusqu'à p = 1619. |
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||
Voir Brève
543
|
Développement
des fractions
périodiques avec identification de la période et de sa longueur. Table pour les
fractions avec un nombre premier pour dénominateur de 2 à 53. |
Exemple
La fraction 1/7
a une période égale à 6: six chiffres qui se répètent indéfiniment. Cette période
142857 est surlignée. |
|
Voir Une
autre présentation de ces fractions
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Retour |
|
|
Suite |
|
|
Voir |
|
|
Site |
|
|
Cette page |
