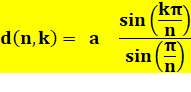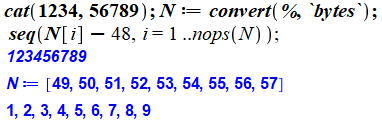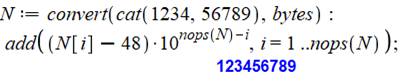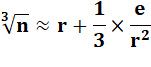NOMBRES – Curiosités, Théorie et Usages Accueil DicoNombre Rubriques Nouveautés Édition du: 03/10/2024 Orientation générale DicoMot Math Atlas Actualités M'écrire Barre de recherche DicoCulture Index alphabétique Références Brèves de Maths
	Maths en se divertissant
Débutants Général	BRÈVES de MATHS									Glossaire Général
INDEX Brèves Atlas des maths	Page 1	Page 10		Page 20		Page 30		Page 40			Page 50

	Page 20 (380-399)		Page 21 (400-419)		Page 22 (420-439)		Page 23 (440-459)		Page 24 (460-479)
	Page 25 (480-499)		Page 26 (500-519)		Page 27 (520-539)		Page 28 (540-559)		Page 29 (560-579)

BRÈVES de MATHS – Page 28

Un millier de faits et chiffres

sur les nombres et les mathématiques

Ces pages sont dédiées à tous ceux qui veulent aborder les mathématiques en douceur et en s'amusant tout en découvrant les aspects les plus fondamentaux de cette discipline. Un parcours à picorer avec nombreux liens d'orientation vers les développements destinés à satisfaire votre curiosité.

En principe ces pages sont très abordables sans connaissances particulières de maths. Elles sont proposées dans un ordre quelconque favorisant la découverte de sujets multiples.

Anglais: Facts and figures about numbers and mathematics

540. Diagonales des polygones

Pour un polygone régulier à n côtés de longueur a, la longueur de la diagonale d se calcule avec cette formule.

Avec k la quantité de côtés interceptés par la diagonale.

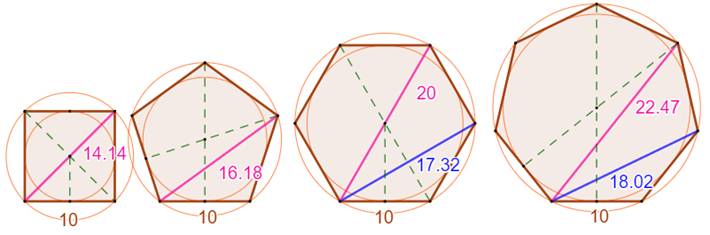
Longueur pour un côté unité

Carré	k = 2	1,414213562	Racine de 2
Pentagone	2	1,618033989	Nombre d'or
Hexagone	2	1,732050808	Racine de 3
	3	2	Nombre 2
Heptagone	2	1,801937735
	3	2,246979603

Illustration avec a = 10

Brèves associées

>>> Diagonales de l'octogone

>>> Diagonales – Quantité

>>> Brèves Géométrie – Index

Pour en savoir plus

>>> Diagonales des polygones

>>> Diagonales des polygones – Table

541. Nombre 1001 – Magie
Pensez à un nombre de trois chiffres. Vous le répétez Montrez sa magie en le divisant par 11, puis par 13, puis par 7. Vous retrouvez le nombre initial.		Exemple 456 456456 / 11 = 41 496 / 13 = 3 192 / 7 = 456		Le secret 7 x 11 x 13 = 1001 abc x 1001 = 1000abc + abc = abcabc
Brèves associées	>>> Nombre 1001 et combinaisons		>>> Brèves Nombres – Index
Pour en savoir plus	>>> Nombre 1001		>>> Magie – Index

542. Nombres Pavés
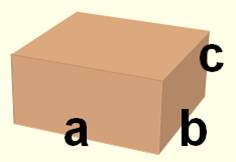
On s'intéresse à la somme des produits des trois nombres entiers a, b et c: N = ab + bc + ca. C'est en fait la moitié de l'aire (S) des six surfaces du pavé droit. Quelles sont les valeurs de S ? A priori toutes les valeurs jusqu'à l'infini. Eh bien, non ! Il existe exactement dix-huit nombres qui résistent: ils ne sont jamais le résultat du calcul de cette formule pour a, b, c positifs.		S = aire des faces du pavé = 2 (ab + bc + ca) Cette aire n'est jamais l'un de ces nombres: {2, 4, 8, 12, 20, 36, 44, 60, 84, 116, 140, 156, 204, 260, 380, 420, 660, 924}
Brèves associées	>>> Nombres narcissiques		>>> Brèves Nombres – Index
Pour en savoir plus	>>> Nombre pavés		>>> Pavé droit

543. Nombre 1 / 103
Toutes les fractions avec 103 au dénominateur possèdent 34 décimales répétitives en trois suites permutées. Le plus petit nombre avec trois suites de chiffres. Chaque fraction développée présente l'une des trois séries de chiffres avec permutations circulaires de ceux- ci. Voir les exemples avec 1000/103 et suivants.
Brèves associées	>>> Nombre 100	>>> Brèves Nombres – Index
Pour en savoir plus	>>> Fractions et développement décimal	>>> Nombre 103

544. Algorithme 196
Algorithme Le procédé consiste à additionner un nombre et son retourné et recommencer avec la somme jusqu'à trouver un palindrome. Exemple en deux itérations		Possible ? Oui, la plupart des nombres se prêtent à ce jeu en plus ou moins d'opérations (itérations). Le nombre 177, par exemple, nécessitera 15 itérations: 177, 948, 1797, 9768, 18447, 92928, 175857, 934428, 1758867, 9447438, 17794887, 96644658, 182289327, 906271608, 1712444217, 8836886388 Cas de 196 À ce jour, les milliards d'itérations n'ont pas permis de trouver un palindrome. C'est le plus petit nombre dans ce cas. Il y a en a d'autres: 295, 394 … 879, … 1997 …
Brèves associées	>>> Motif itératif en 98 et 99 >>> Procédé de Kaprekar		>>> Brèves Motifs – Index
Pour en savoir plus	>>> Algorithme 196 >>> Nombres retournés		>>> Nombre 177 >>> Nombre 196

545. Régions externes des polygones
Combien de régions polygonales sont formées par le prolongement des côtés d'un polygone, ici un dodécagone (rouge) ? La figure de droite montre le principe du dénombrement: trait rouge issu du sommet: 3 régions dont une ouverte, et trait noir issu du côté: 3 régions dont une ouverte. Bilan: 12 fois (3 + 3) + la région centrale = 73 régions polygonales dont 49 fermées.
Brèves associées	>>> Octogone – Diagonales	>>> Brèves géométrie – Index
Pour en savoir plus	>>> Régions externes des polygones	>>> Polygones – Introduction et index

546. Pentagone Meccano
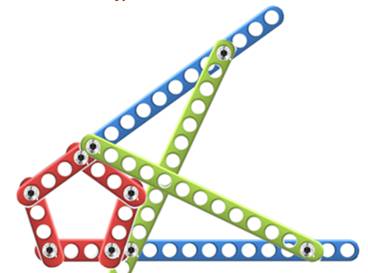
Défi Il s'agit d'un défi numérique. Comment rigidifier le pentagone en utilisant des barres, trouées régulièrement du style de celles du jeu de construction Meccano. Autrement-dit : trouver un montage tel que toutes les longueurs soient des nombres entiers. Magie du nombre d'or On sait que le nombre d'or se niche dans le pentagone. Ici, un calcul fait intervenir ses puissances et finissent par donner des nombres entiers malgré le caractère irrationnel du nombre d'or.		Côté du pentagone: 3 (pour 4 trous) Fixation sur barres bleues: 12 et 4 Longueur sur barres vertes: 11
Brèves associées	>>> Pentagone >>> Nombre d'or		>>> Brèves construction – Index
Pour en savoir plus	>>> Pentagone rigide façon Meccano		>>> Polygones – Introduction et index

547. Procédé de Kaprekar
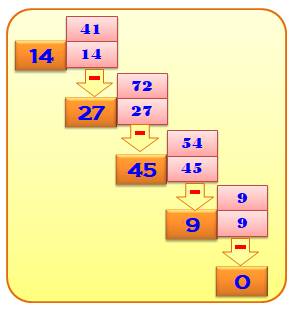
Procédé itératif qui consiste à ordonner les chiffres d'un nombre par ordre décroissant (Max) et également par ordre croissant (Min) et à effectuer leur soustraction (D = Max – Min). La différence (D) est soumise à nouveau à ce même procédé. Exemple Par ce procédé le nombre 14 devient 27, puis 45 puis 9 puis 0 et le procédé prend fin. Le cycle de Kaprekar de 14 est: [14, 27, 45, 9, 0]. Le cycle de Kaprekar de 41 est le même. La longueur du cycle est égale à 5. Le nombre final est 0. Observez que 14 devient 27 = 9(4 – 1); un multiple de 9.
Brèves associées	>>> Motif itératif en 98 et 99	>>> Brèves opérations – Index
Pour en savoir plus	>>> Procédé de Kaprekar	>>> Motifs – Index

548. Cycle des chiffres au carré
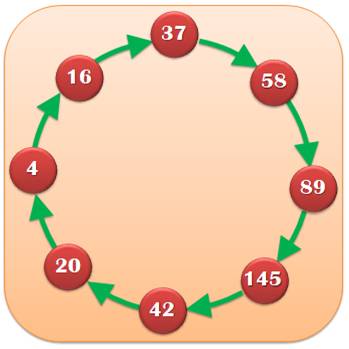
Mise en évidence de la destinée des nombres par calcul de la racine additive au carré. Celle-ci consiste, comme pour la preuve par neuf à ajouter les chiffres, mais au carré. On applique le même calcul de manière itérative sur les chiffres du résultat. Exemple avec 4 Avec le nombre 4 au départ, le procédé conduit à un cycle revenant sur le nombre 4 lui-même. 4² = 16 1² + 6² = 1 + 36 = 37 3² + 7² = 9 + 49 = 58 etc. Règle générale Pour tout nombre le procédé se termine par une boucle en 4, ou alors il finit par le nombre 1.		Le cycle en 4 La fin en 1 Avec 31, on aurait: 3² + 1² = 10 et 1² + 0² = 1 et Arrêt. Essayez avec le nombre tout simple: 1112.
Brèves associées	>>> Somme des carrés des entiers		>>> Brèves opérations – Index
Pour en savoir plus	>>> Cycle des chiffres au carré >>> Racine additive		>>> Carrés – Index

549. Cycle 3x + 1 – Syracuse
Séquence Il s'agit d'une séquence très simple d'opérations sur les nombres qui ramène toujours au même endroit, le nombre 1. D'abord un amusement, cette étonnante suite est devenue troublante pour les mathématiciens qui ne se lassent pas de l'explorer sans avoir encore réussi à la domestiquer. Exemple avec 5 au départ 5 impair => 3 x 5 + 1 = 16 16 pair => 8, puis 4, 2, 1 Conjecture Pour tout nombre, la fin de cycle est 1.		Règle du jeu
Brèves associées	>>> Multiplication autour de 100		>>> Brèves Itérations – Index >>> Brèves Opérations – Index
Pour en savoir plus	>>> Cycle 3x + 1, suite de Syracuse		>>> Suite

550. Caractérisation des carrés
Un nombre n'est pas un carré s'il ne se termine pas par: 00, 01, 21, 41, 61, 81, 04, 24, 64, 84, 25 16, 36, 56, 76, 96 09, 29, 49, 69, 89 Les nombres qui se terminent de la sorte sont susceptibles d'être carrés. De 1 à 100, ce sont (en rouge, les vrais carrés): 1, 4, 9, 16, 21, 24, 25, 29, 36, 41, 44, 49, 56, 61, 64, 69, 76, 81, 84, 89, 96, 100		Critère de reconnaissance d'un possible carré Un critère supplémentaire: la racine numérique d'un carré ne peut être que: {1, 4, 7, 9}.
Brèves associées	>>> Carrés et le nombre 5		>>> Brèves opérations – Index
Pour en savoir plus	>>> Racine numérique des puissances		>>> Racine numérique

551. "Premiers" nombres premiers

Os d'Ishango

Les plus anciennes traces des nombres premiers ont été trouvées près du lac Édouard au Zaïre (Congo), non loin des sources du Nil. Il s'agit d'un os de plus de 20 000 ans, appelé l'os d'Ishango, découvert en 1950.

Cet os qualifié de «plus vieil objet mathématiques de l'humanité», exposé au Muséum des sciences naturelles de Bruxelles, est recouvert d'entailles représentant les nombres 11, 13, 17 et 19 (avec beaucoup d'imagination !). Ces nombres sont premiers : est-ce un hasard ou l'ébauche d'une table de nombres premiers ? La question reste ouverte.

Les Grecs

Le grec Pythagore (-580 à -490) fonde l’école Pythagoricienne qui va durer environ 10 générations. Ces passionnés par l'Arithmétique étudient la notion de diviseur et découvrent les nombres parfaits.

Sans lui donner ce nom, les nombres premiers devaient donc être connus par Pythagore et ses adeptes.

Dans les écrits de Philolaos (env. -470 à -390), les nombres premiers sont cités comme une classe particulière de nombres.

La première allusion concrète aux nombres premiers est faite par Aristote (-384 à -322) dans un passage de ses Seconds analytiques. Dans la Métaphysique, il distingue le composé et l'incomposé et "l'incomposé vient avant le composé".

Savants arabes

Le grand savant arabe, Ibn al-HAYTHAM ou ALHAZEN (né à Bassora en Irak actuelle en 965, mort au Caire en 1039) établit que :

si p est un nombre premier alors n = (p – 1)! + 1 est divisible par p.

Cette propriété est connue sous le nom de théorème de Wilson.

Exemple avec p = 7:

6! = 720, et 721 / 7 = 103.

Soit le tableau:

p = 2	n = 2	n / p = 1
3	3	1
5	25	5
7	721	103
11	3628801	329891

Brèves associées

>>> Diviseurs d'un nombre

>>> Brèves premiers – Index

Pour en savoir plus

>>> Historique des nombres premiers

>>> Théorème de Wilson

>>> Alhazen et ses contemporains

>>> Nombres parfaits

552. Date Palindrome

Dates dont les nombres concaténés forment un palindrome.

Format: les jours et les mois sont écrits avec quatre chiffres en ajoutant des 0 si nécessaire ou alors seul le mois est complété à deux chiffres. Il existe aussi le format américain avec l'année en tête, format bien pratique pour le classement chronologique.

Avec le format 01 02 2021, il a 145 dates palindromes jusqu'à 1000 et 121 entre 1000 et 3000.

Grands sauts de huit siècles !

Aucune date palindrome

du 29 10 192

au 10 01 1001

du 29 11 1192

au 10 02 2001

Dans les deux cas:

808 a 2 m 12 j

= 9 698 m 12 j

= 295 182 j

= 7 084 368 h

= 425 062 080 min

= 25 503 724 800 s

Format 01 02 2021

21	2	2012	21022012
2	2	2020	02022020
12	2	2021	12022021
22	2	2022	22022022
3	2	2030	03022030

Format 1 02 2021

9	10	2019	9102019
12	2	2021	12022021
22	2	2022	22022022
13	2	2031	13022031

Format 2021 02 01

2011	11	2	20111102
2020	2	2	20200202
2021	12	2	20211202
2030	3	2	20300302

Brèves associées

>>> Palindromes

>>> Brèves motifs – Index

Pour en savoir plus

>>> Dates palindromes

>>> Palindromes

>>> Calendrier

>>> Année 2021 avec humour

553. Outils mathématiques Google
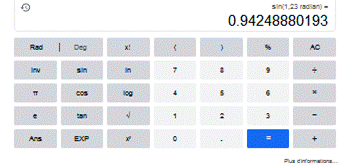
Google offre quelques outils mathématiques bien utiles. Par exemple, tapez sin(1,23) et vous obtenez le résultat sur la calculatrice scientifique de Google. Avec 3x^2 + x – 5 = 0, l'équation est résolue (y compris affichage des étapes): Avec le navigateur Google Chrome, de nombreuses extensions mathématiques sont disponibles.		Image animée obtenue en tapant simplement sin(x)/y
Brèves associées	>>> Calculatrice		>>> Brèves outils – Index
Pour en savoir plus	>>> Outils informatiques		>>> Calculette

554. Conversion chaine en nombre
Programmes Maple			Principe La conversion du type byte d'une chaine de caractères produit une liste d'entiers. Notamment les chiffres sont isolés sous la forme d'un nombre égal au chiffre + 48.
			Exemple d'application Supposons que l'on veuille convertir une chaine de caractères (string) représentant un nombre en un nombre entier (integer). La chaine a été obtenue à la suite d'une concaténation (cat). N reçoit la liste des nombres. Pour retrouver les chiffres, il suffit retirer 48 à chacun des nombres indicés par i de 1 à la quantité de nombres dans la liste (nops).
				Ici, au lieu d'énoncer les chiffres, on les additionne avec une pondération en puissance de 10 pour reconstituer le nombre complet.
		Conversion chaine de caractères en un nombre entier Il existe une solution plus simple avec l'instruction parse (analyser). Dans le premier cas, la chaine de caractères ("…") est convertie en un nombre prêt pour des calculs. Dans le second cas, la concaténation produit une chaine de caractères qui est convertie en nombre par parse.
Brèves associées	>>> Programmation				>>> Brèves informatiques – Index
Pour en savoir plus	>>> Trucs de programmation Maple				>>> Programmes – Index

555. Notion de "2" cachée
Préfixe Latin BI- AMBO- Grec DI- AMPHI- Gotique TWAI		"2" caché Balance Besace Bief Biner Biscuit Brouette Dièse Dilemme Duplex Janus	Exemple de "2" bien caché Tête-bêche: mot invariable à deux accents circonflexes. Vient de Tête-Béchevet, avec béchevet ou bêchevet qui désigne un double chevet (un lit à béchevet, à deux endroits pour poser la tête) ou encore dormir à béchevet (dormir l'un la tête aux pieds de l'autre). Du latin biceps (à deux têtes, bicéphale) Anglais: head to tail.
Brèves associées	>>> Les nombres 4 et 8 en chinois			>>> Brèves Langue – Index
Pour en savoir plus	>>> Nombre 2 – Culture >>> Quantité 2 – Linguistique			>>> DicoNombre – Nombre 2 >>> DicoCulture – Tête-bêche

556. Somme de produits
Une règle bien pratique pour calculer la somme de n termes, chacun étant le produit de h facteurs consécutifs. Exemple et règle pratique de calcul Somme de n termes de h facteurs = fraction 1/(h+1) du produit commençant par n et comptant h+1 facteurs (c'est aussi le dernier terme avec un facteur en plus). Autres exemples S₃ (3) = 1x2x3 + 2x3x4 + 3x4x5 = 1/4 (3x4x5x6) = 90 S₅ (5) = 1x2x3x4x5 + 2x3x4x5x6 + … + 5x6x7x8x9 = 1/6 (5x 6x7x8x9x10) = 25 200
Brèves associées	>>> Produit de deux nombres proches	>>> Brèves Calculs – Index
Pour en savoir plus	>>> Somme de produits	>>> Somme des entiers

557. Racine cubique – Calcul mental
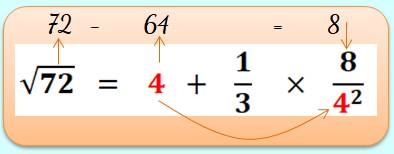
Méthode Pour calculer, par exemple, la racine cubique de n = 72: Chercher le cube le plus proche (64 = 4³): r = 4; Son écart avec le nombre cherché: (e = 72 – 64 = 8); Calculer cette opération => Formule générale		Calcul approché de la racine cubique de 72 Ce calcul donne: 4 + 1/6 = 4,166… pour la valeur exacte: 4,160…
Brèves associées	>>> Racine cubique (deux chiffres)		>>> Brèves Calculs – Index
Pour en savoir plus	>>> Racine cubique – Méthode de Newton		>>> Calcul mental – Index

558. Tour de magie – Simple !

Le tour

Pensez à un nombre.

Multipliez par 2.

Ajoutez 10.

Divisez par 2.

Retranchez le nombre de départ.

Vous annoncez:
"Le résultat est 5 n'est-ce pas ?"

Explication

Pensez à un nombre:	n
Multipliez par 2:	2n
Ajoutez 10:	2n + 10
Divisez par 2:	n + 5
Retranchez le nombre de départ:	5

Finalement, le nombre de départ est éliminé lors des calculs.

Brèves associées

>>> Multiplication magique par 91

>>> Brèves Magie – Index

Pour en savoir plus

>>> Nombre 5

>>> Magie – Index

559. Multiplication et division mentales par 9
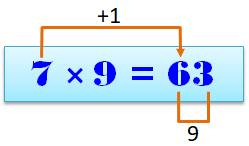
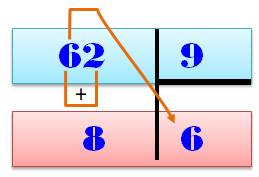
Multiplication de n par 9 Dizaine = n – 1 Unité = Complément à 9 de la dizaine		Division par 9 Quotient = dizaine Reste = somme des deux chiffres (tenir compte de la retenue éventuelle) Méthode valable pour un nombre quelconque de chiffres

Brèves associées	>>> Multiplication proches de 100		>>> Brèves Calcul mental – Index
Pour en savoir plus	>>> Division par 9, 19 … - Explications >>> Nombre 9		>>> Calcul mental – Index

Retour	Brèves de maths – Page 27
Suite	Brèves de maths – Page 29
Voir	Voir liens en haut de page
Cette page	http://villemin.gerard.free.fr/NombDico/aBreves/Breve28.htm

540. Diagonales des polygones

541. Nombre 1001 – Magie

542. Nombres Pavés

543. Nombre 1 / 103

544. Algorithme 196

545. Régions externes des polygones

546. Pentagone Meccano

547. Procédé de Kaprekar

548. Cycle des chiffres au carré

549. Cycle 3x + 1 – Syracuse

550. Caractérisation des carrés

551. "Premiers" nombres premiers

552. Date Palindrome

553. Outils mathématiques Google

554. Conversion chaine en nombre

555. Notion de "2" cachée

556. Somme de produits

557. Racine cubique – Calcul mental

558. Tour de magie – Simple !

559. Multiplication et division mentales par 9