|
|||||||||||||||||||||||||||||||||||
![]()
|
CALCUL sans machine de la RACINE CARRÉE Les calculateurs prodiges
excellent dans ce genre de sport ! Deux cas se présentent: le nombre
considéré est lui-même une puissance exacte du nombre à chercher ou il ne
l'est pas. Ici, on donne une méthode de
calcul mental pour la racine carrée
d'un nombre que ce nombre soit un carré ou non. Un rappel sur la bonne
vieille méthode de calcul posé comme la division. Une méthode efficace mais
lourde consiste à utiliser les fractions
continues. Pour finir, une curiosité de
calcul de la racine avec les impairs. Comme pour beaucoup de
calculs, la méthode par recherche-erreur (dichotomie)
est toujours possible. Note: nous travaillons dans le monde des nombres positifs (pour éviter les
questions sur la valeur négatives d'une raine carrée). |
Voir au préalable calcul rapide des carrés
Un truc marrant!
|
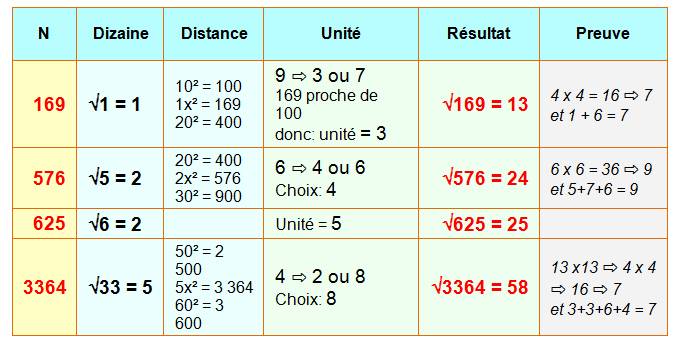
Pour
calculer la racine d'un carré parfait, il suffit de compter combien il faut
ajouter de nombres impairs consécutifs pour atteindre ce nombre.
|
Suite Méthode semblable
si le carré n'est pas parfait
Calcul rapide
|
Formule pour approcher
une racine carrée.
|
|
|
|
||
|
Calcul avec Pythagore Remarquez que R = (n+1) / 2
|
Si le segment
unité mesure m, alors la perpendiculaire mesure |
|
Voir Autre vision / Pseudo quadrature du cercle
|
|
|
|
Calculez la racine carrée de 1444. On note N = mcdu (milliers,
centaines, dizaines et unités).
Mentalement la preuve par 9 peut s'avérer
utile. 38 x 38 = 1444 Dans le monde des racines
numériques (3 + 8) (3 + 8) = (1 + 4 + 4 +4) 2 x 2 = 4 BON! Autres
exemples
|
|
|
|
|
|
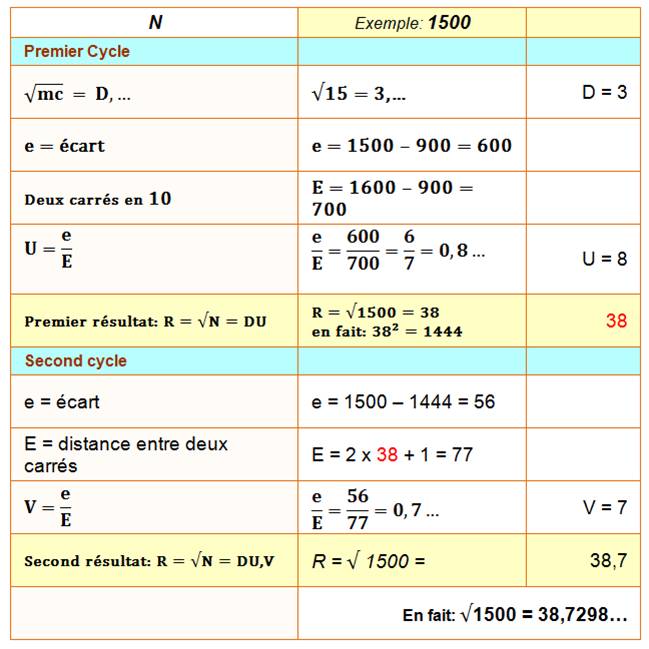
Calcul pour des nombres à
quatre chiffres. Calculer avec un chiffre
après la virgule peut s'envisager, au-delà, il faut être très doué!
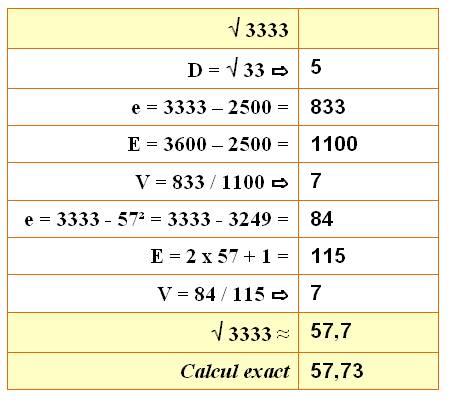
Autre
exemple avec 3 333
Note: Le calcul d'une
proportion (e/E) pour en déduire le chiffre suivant n'est qu'une
approximation commode pour le calcul mental; la progression n'est pas
linéaire, mais, bien sûr, quadratique. Le résultat est néanmoins satisfaisant
dans la majorité des cas. On le vérifie en recalculant le carré. |
|
|
|
|
|
Calculer la racine carrée
n'est pas plus compliqué qu'effectuer une division. C'est tout aussi fastidieux.
Mais ce fut le seul moyen avant l'arrivée des calculatrices.
Cette méthode donnant les
chiffres de la racine les uns après les autres était connue des Chinois. Les Neuf chapitres sur les procédures mathématiques
(vers le début de notre ère) rassemble toutes les mathématiques de la Chine
ancienne. Liu Hui (263) commente ce livre et surtout donne une interprétation géométrique de la méthode. |
|
Un calcul complet avec décimales
La
présentation est éclatée (plus claire selon moi) par rapport à la méthode
enseignée autrefois.

Bilan: racine de 1234,54 = 35,136 306 009 …
|
|
|||
|
Nombres de 2 chiffres |
N = du |
|
|
|
Nombres de 4 chiffres |
N = 100C + U R = 10d + u |
2025 = 100 x 20 + 25 45 =
10x4 + 5 |
|
|
R² = 100d² + 2x10du + u² |
2025 = 100x4² +
2x10x4x5 + 5² =
1600 + 400
+ 25 |
||
|
Illustration Où apparaissent:
|
|
||
|
On connait l'aire du très
grand carré. |
N = (10d + u)² |
A = 2025 |
|
|
On peut extraire le plus
grand carré parfait qui y est inscrit. |
N = 100C +
U N = 100d² + … En associant C et d² |
Carré de 40 de côté |
|
|
Estimer la taille des
rectangles. |
N – 100d² = 2x10du + … |
2025 – 1600 = 425 2 x 10 x 4 x u + … =
425 u = 425/(80 +…) u = 5,… |
|
|
Bilan après le .retrait des
rectangles |
N – 100d² – 2x10du = R |
d = 4 et u = 5 425 – 2x40x5 = 25 |
|
|
Chiffre des unités. |
R = u² |
25 = 5² |
|
|
|
|
|
Cette méthode est générale à
beaucoup de calcul. Il s'agit de cerner la valeur recherchée en encadrant la
réponse de plus en plus finement. Calculons la racine de 60 =
7,745 966 692 414 833 770 358 530 799 564 8 …
Méthode qui est pratique
lorsqu'on dispose d'une calculette sans la fonction racine carrée. |
|
|
|
|||
|
Une propriété exceptionnelle
des carrés: ils sont somme des
impairs consécutifs. Ex: 25 = 1 + 3 + 5 + 9; ajoutez 11 et vous obtenez un nouveau carré: 25 + 11
= 36 = 6². Pour obtenir n², on ajoute
les impairs consécutifs de 1 à 2n – 1. La méthode d'extraction de
racine carrée utilisant cette propriété est aujourd'hui une curiosité. Elle
était utilisée sur les machines à calculer mécaniques à manivelle. On cherche la racine de 17
qui vaut 4,123 105 625 617 660 549 821 409 855 974 1… |
|||
|
Retirons autant d'impairs
que possible |
17 – 1 – 3 – 5 – 7 = 1 |
4 impairs |
|
|
Travail sur le reste |
1 suivi de la tranche de deux chiffres suivants. |
1 00 |
|
|
Impair suivant |
(7
+ 1) x 10 + 1 |
81 |
|
|
Retrait des impairs |
100 – 81 = 19 |
1 impair |
|
|
Travail sur le reste |
Nouvelle tranche de 00 |
19 00 |
|
|
Impair suivant |
(81
+ 1) x 10 + 1 |
821 |
|
|
Retrait des impairs |
1900 – 821 – 823 = 256 |
2 impairs |
|
|
Travail sur le reste |
|
256 00 |
|
|
Impair suivant |
(823
+ 1) x 10 + 1 |
8241 |
|
|
Retrait des impairs |
25 600 – 8 241 – 8 243 – 8 245 = 871 |
3 impairs |
|
|
Etc. |
La racine de 17 commence par |
4, 123 |
|
|
Le passage à la tranche supérieure
de deux chiffres correspond au passage au chiffre suivant de la racine. Soit
10n pour la racine ou (10n)² pour le nombre; lequel est atteint par la somme
des nombres impairs de 1 à 20n – 1. Ce nombre peut se développer en: ((2n – 1) + 1) x 10 + 1. D'où le calcul un peu
curieux présenté dans l'algorithme. |
|||
![]()
|
Retour |
|
|
Suite |
|
|
Voir |
|
|
Cette page |
![]()