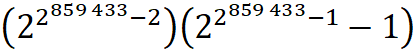|
|||||||||||||||||||||||||||||
![]()
|
NOMBRES PARFAITS – Liste Mersenne: M(p) = 2p – 1 Parfait: P(p) = 2p – 1 (2p – 1) |
|
Chiffres dans |
|
|
|
||||
|
N° |
p |
Mp |
Pp |
Année |
Découvreurs |
Valeur |
|
|
1 |
2 |
1 |
1 |
---- |
|
||
|
2 |
3 |
1 |
2 |
---- |
|
||
|
|
|
||||||
|
3 |
5 |
2 |
3 |
---- |
|
||
|
4 |
7 |
3 |
4 |
---- |
|
||
|
|
|
||||||
|
5 |
13 |
4 |
8 |
1456 |
|
33 550 336 |
|
|
|
|
||||||
|
6 |
17 |
6 |
10 |
1588 |
Cataldi |
8 589 869 056 |
|
7 |
19 |
6 |
12 |
1588 |
Cataldi |
137 438 691 328 |
|
8 |
31 |
10 |
19 |
1750 |
Euler |
2 305 843 008 139
952 128 |
|
9 |
61 |
19 |
37 |
1883 |
Pervouchine |
2 658 455 991 569 831 744 654 692 615 953 842 176 |
|
10 |
89 |
27 |
54 |
1911 |
Powers |
|
|
11 |
107 |
33 |
65 |
1914 |
Powers |
|
|
127 |
39 |
77 |
1876 |
Lucas |
|
|
|
|
|
|||||
|
Chiffres dans |
|
|
|||
|
N° |
p |
Mp |
Pp |
Année |
Découvreurs |
|
13 |
521 |
157 |
314 |
1952 |
Robinson |
|
|
|||||
|
14 |
607 |
183 |
366 |
1952 |
Robinson |
|
15 |
1 279 |
386 |
770 |
1952 |
Robinson |
|
16 |
2 203 |
664 |
1 327 |
1952 |
Robinson |
|
17 |
2 281 |
687 |
1 373 |
1952 |
Robinson |
|
18 |
3 217 |
969 |
1 937 |
1957 |
Riesel |
|
19 |
4 253 |
1 281 |
2 561 |
1961 |
Hurwitz &
Selfridge |
|
20 |
4 423 |
1 332 |
2 663 |
1961 |
Hurwitz &
Selfridge |
|
21 |
9 689 |
2 917 |
5 834 |
1963 |
Gillies |
|
22 |
9 941 |
2 993 |
5 985 |
1963 |
Gillies |
|
23 |
11 213 |
3 376 |
6 751 |
1963 |
Gillies |
|
24 |
19 937 |
6 002 |
12 003 |
1971 |
Tuckerman |
|
25 |
21 701 |
6 533 |
13 066 |
1978 |
Noll & Nickel |
|
26 |
23 209 |
6 987 |
13 973 |
1979 |
Noll |
|
27 |
44 497 |
13 395 |
26 790 |
1979 |
Nelson &
Slowinski |
|
28 |
86 243 |
25 962 |
51 924 |
1982 |
Slowinski |
|
29 |
110 503 |
33 265 |
66 530 |
1988 |
Colquitt &
Welsh |
|
30 |
132 049 |
39 751 |
79 502 |
1983 |
Slowinski |
|
31 |
216 091 |
65 050 |
130 100 |
1985 |
Slowinski |
|
32 |
756 839 |
227 832 |
455 663 |
1992 |
Slowinski &
Gage |
|
33 |
859 433 |
258 716 |
517 430 |
1994 |
Slowinski &
Gage |
|
34 |
1 257 787 |
378 632 |
757 263 |
1996 |
Slowinski &
Gage |
|
35 |
1 398 269 |
420 921 |
841 842 |
1996 |
(GIMPS) |
|
36 |
2 976 221 |
895 932 |
1 791 864 |
1997 |
(GIMPS) |
|
37 |
3 021 377 |
909 526 |
1 819 050 |
1998 |
(GIMPS, PrimeNet) |
|
38 |
2 098 960 |
4 197 919 |
1999 |
(GIMPS) |
|
|
39 |
13 466 917 |
4 053 946 |
8 107 892 |
2001 |
GIPMS |
|
… |
|
||||
|
49 |
74 207 281 |
44 677 235 |
2016 |
Cooper, Woltman,
Kurowski, Blosser, et al. |
|
|
50 |
77 232 917 |
2017 |
Pace, Woltman,
Kurowski, Blosser, et al |
||
|
51 |
82 589 933 |
2018 |
Laroche, Woltman,
Kurowski, Blosser, et al. |
||
|
|
|
||||
Voir
sites indiqués pour liste complète
SUITE
en Nombres premiers records
La "tête" du Mersenne le plus grand connu en 1997
|
|
Voir Ce nombre dans
le DicoNombre
![]()
|
Suite |
|
|
Voir |
|
|
|
|
|
Cette page |
http://villemin.gerard.free.fr/Wwwgvmm/Decompos/ParfList.htm |
![]()