NOMBRES – Curiosités, Théorie et Usages Accueil DicoNombre Rubriques Nouveautés Édition du: 18/12/2021 Orientation générale  DicoMot Math Atlas Actualités M'écrire Barre de recherche DicoCulture Index alphabétique Références Brèves de Maths
	Diviseurs
Débutants Nombres	Types de nombres selon leurs diviseurs			Glossaire Diviseurs
INDEX Décomposition Diviseurs	Débutants	Présentation	Parfait	Amiables
		Sommaire de cette page >>> Mise en paquets >>> Cas du 6 >>> Les quatre types >>> Somme des diviseurs >>> Les types de nombres

NOMBRES PARFAITS

Bases, pas à pas

Comment aborder les nombres et leurs diviseurs? La somme des diviseurs? Comparaison de cette somme au nombre initial? Etc.

Pourquoi 6 et 28 sont deux nombres si particuliers?

MISE EN PAQUETS
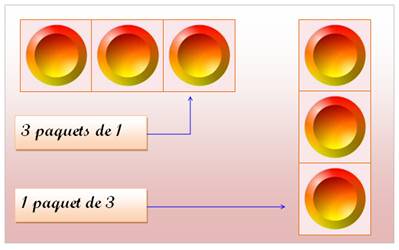
Nombre 3	Le nombre 3 peut être vu de deux manières: Trois paquets de "une unité". Oui, bon cet arrangement est naturel puisque c'est la définition même des nombres: "3" veut dire trois objets. Un paquet de trois. Certes, guère plus original, mais on va tout de même conserver cette présentation par la suite. Pour la suite, nous laissons de côté le banal cas de 3 paquets de 1.
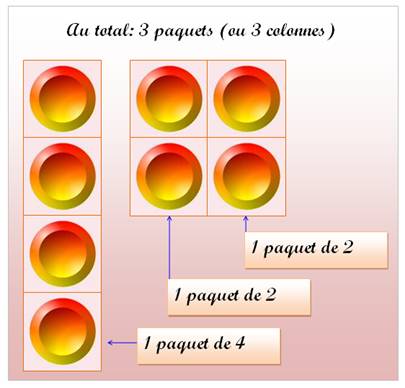
Nombre 4	Nous laissons de côté les 4 paquets de 1, comme indiqué. Il reste, en fait, deux manières de "mettre en paquets" le chiffre 4. Au total, comme on le voit sur la figure, on compte 3 paquets. Curieuse façon de compter, mais laissons-nous guider.
Nombre 5	Peu intéressant! Un seul paquet de 5.

Nombre 6

Il y a 3 manières de "mettre en paquets" le nombre 6. Au total on compte 6 paquets, autant que le nombre lui-même. Extraordinaire! Le 6 peut se mettre en 6 paquets. C'est un nombre parfait. Déflorons un peu le sujet: le nombre 6 est divisible par 1, par 2 et par 3. Et la somme de ces trois nombres ( 1 + 2 + 3) est précisément égale au nombre initial 6.

Voir une autre manière imagée du nombre parfait: Illustration en parts de gâteau

Les quatre types de nombres
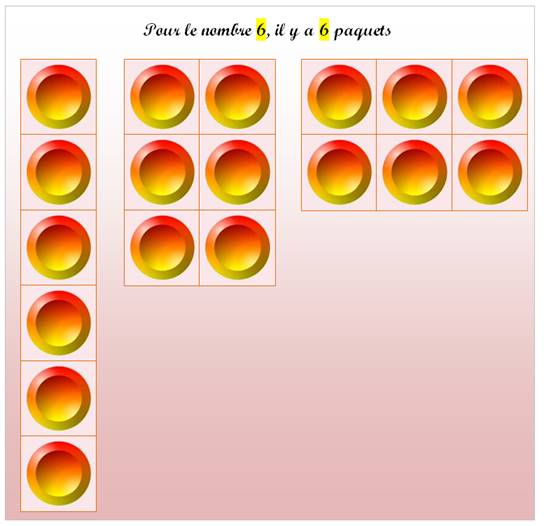
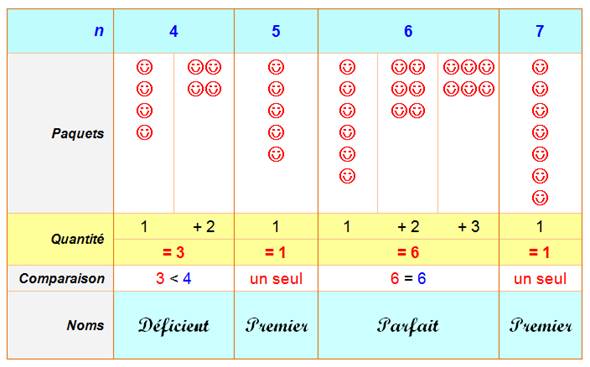
Nombres 4 à 7	Récapitulons: Un seul paquet possible: nombre premier. Autant de paquets que le nombre: nombre parfait. Moins de paquets que le nombre: nombre déficients.
Nombres 8 et 12	Le nombre 12 crée plus de paquets: nombre abondant.

SOMME DES DIVISEURS

Quantité de paquets = Somme des diviseurs Vous aurez aisément reconnus que ce qui est appelé paquets caractérise la possibilité de diviser le nombre Par exemple: 8 est divisible par 1, 2 et 4. 1, 2 et 4 sont les diviseurs stricts de 8. 1, 2, 4 et 8 sont les diviseurs de 8. Remarquez que la quantité de paquets ou de colonnes sur les exemples est égale à la somme des diviseurs propres. Somme des diviseurs propres: 1 + 2 + 4 = 7 Cette somme est inférieure à 8. Le nombre 8 est dit déficient. Cette manière de comparer les nombres à la somme de leurs diviseurs permet de classer les nombres selon plusieurs types.

TYPES de nombres selon la somme des diviseurs
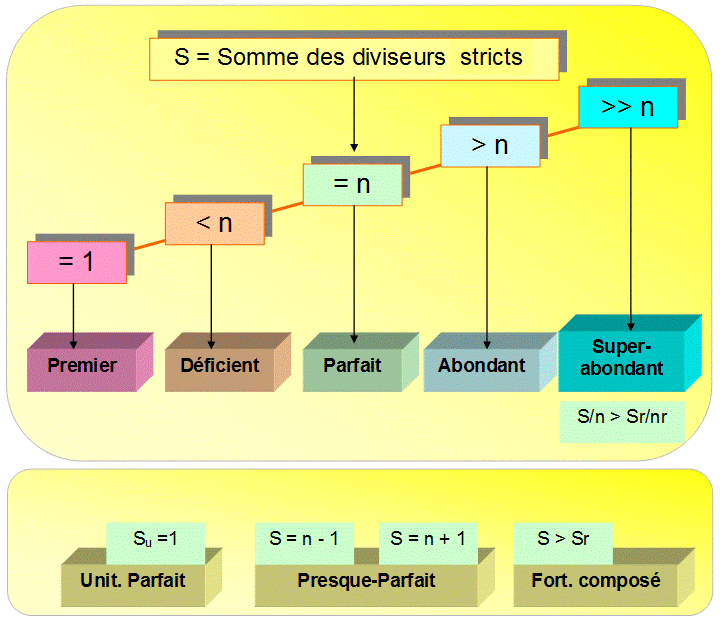
Suite générale >>> Suite selon le type de nombre: Premier / Déficient / Parfait / Abondant / Superabondant Unitairement parfait / Presque-parfait / Fortement composé Types de nombres selon leurs diviseurs

Suite	Comparaison bons et parfaits Abondants, parfaits et déficients Voir haut de page
Voir	Calcul mental – Index Carrés Magiques Débutants – Index Géométrie – Index Géométrie – Index Humour – Index Jeux – Index Nombres économes, équidistants et prodigues Nombres magiques – Index Semi-parfaits Tables abondants / déficients Théorie des nombres – Index
Cette page	http://villemin.gerard.free.fr/Wwwgvmm/Decompos/ParfDebu.htm