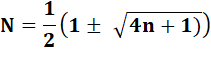NOMBRES – Curiosités, Théorie et Usages Accueil DicoNombre Rubriques Nouveautés Édition du: 24/06/2023 Orientation générale  DicoMot Math Atlas Actualités M'écrire Barre de recherche DicoCulture Index alphabétique Références Brèves de Maths
	PUISSANCE & RACINES
Débutants Général	RACINES CONTINUES			Glossaire Général
INDEX Racines carrées Analyse Puissance	Racine	Racine continue	Nombre d'or	Tous les nombres
			Zéro	Ramanujan
		Sommaire de cette page >>> Approche avec 2 >>> FORMULE pour tous les nombres >>> FORMULE INVERSE >>> Autres fraction – Exemple pour 3

RACINES CONTINUES

On peut écrire les nombres entiers sous la forme d'une suite de radicaux imbriqués sans fin.

Anglais: Nested radical / Nested square roots / Continued roots / Continued radical

Radicaux imbriqués

Simplifier une expression avec radicaux imbriqués est généralement un problème difficile.

Certains cas (rares) sont néanmoins calculables, comme:

Simplifier:
Tout sous le second radical:
Possible que si cette quantité est un carré (sa racine est rationnelle):
Relation simplifiée:
Simplification:

Voir Racines continues / Radical

Approche avec 2
Racine continue de 2 Convergence Après 12 itérations: Écart = 0, 000 000 261	Calculs successifs 1, 414 1, 847 1, 961 1, 990 1, 997 1, 99939 1, 99984 1, 99996 1, 9999905 1, 9999976 1, 9999989 1, 999999739

Voir Résolution par équation

RACINE CONTINUE pour tous les nombres
Formule générale
Démonstration Ajoutons n de chaque côté
Prenons la racine carrée de chaque côté
Or, la partie de droite est notre expression d'origine
Passons au carré
Et la valeur du nombre n sous le radical est donnée par cette relation: Voir Nombre pronique

Voir Brève 51 -1010

Application

N	n	Racines continues
2	1 x 2
3	2 x 3
4	3 x 4
Notation abrégée		5 = rc en 4 x 5 = 20 6 = rc en 5 x 6 = 30 …

Théorème

Tout nombre entier N est exprimable sous forme d'une racine continue

dont la valeur sous le radical est égale à = (N-1) N

FORMULE INVERSE

Je me donne le nombre sous le radical. Que vaut la racine continue ?

Résolution d'une équation de 2^e degré

Quelques résultats

n	N1	N2
0	1	0	Voir Zéro
1	1, 618033989	-0, 6180339890	Voir Nombre d'or
2	2	-1
3	2, 302775638	-1, 302775638
4	2, 561552813	-1, 561552813
5	2, 791287848	-1, 791287848
6	3	-2
7	3, 192582404	-2, 192582404
8	3, 372281324	-2, 372281324
9	3, 541381265	-2, 541381265
10	3, 701562119	-2, 701562119

Autres fraction – Exemple pour 3
3 = Les coefficients sont les entiers successifs.
4 = Sur le même principe

Quelques trouvailles de Ramanujan

Suite	Fractions continues Ramanujan et 1729 – Nombre Taxicab
Voir	Fractions continues Nombres rationnels … Nombres périodiques Suite de Farey et calendriers
DicoNombre	Nombre 2 Nombre 3
Sites	Radical imbriqué – Wikipédia Pi-Formulas and gray code – Pierluigi Vellucci and Alberto Maria Bersani Nested Radical – Wolfram MathWorld
Cette page	http://villemin.gerard.free.fr/Wwwgvmm/Nombre/Racinint.htm