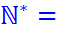NOMBRES – Curiosités, Théorie et Usages Accueil DicoNombre Rubriques Nouveautés Édition du: 12/11/2024 Orientation générale  DicoMot Math Atlas Actualités M'écrire Barre de recherche DicoCulture Index alphabétique Références Brèves de Maths
	NOMBRES / TYPES
Débutants Types de Nombres	INVENTAIRE				Glossaire Nombres
INDEX Types de nombres	Inventaire	Entiers		Irrationnels		Algébriques
	Inventaire – Graphe		Bref aperçu narratif (fr-ang.)			Transcendants
		Sommaire de cette page >>> Classification des nombres >>> Tableau des types de nombres (ensembles) >>> Propriétés

Trois scientifiques - un ingénieur, un biologiste et un mathématicien - discutent sur la terrasse d'un pub. Ils remarquent que deux personnes entrent dans une maison située en face du café, qu'ils imaginent vide. Une heure plus tard, trois personnes en sortent. L'ingénieur donne l'explication suivante : - Les données initiales étaient erronées. Le biologiste lance quant à lui : - C'est simple, ils se sont reproduits. Et le mathématicien de conclure : - Si une personne entre de nouveau dans la maison, elle redeviendra vide... >>>

Par nombre, nous entendons non pas une multitude d'unités, mais plutôt le rapport d'une quantité quelconque à une autre quantité de même sorte, que nous prenons comme unité. By number we understand not so much a multitude of unities, as the abstracted ratio of any quantity to another quantity of the same kind, which we take for unity Newton – Universal Arithmetic - 1728

Voir Pensées & humour

CLASSIFICATION DES NOMBRES

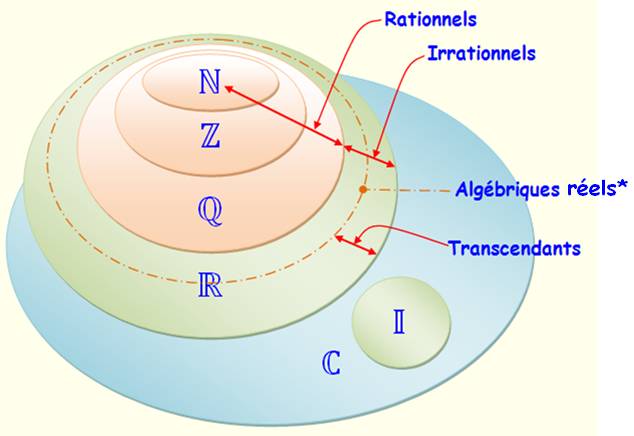
Types de nombres

Les nombres entiers naturels (N) sont les nombres ordinaires pour compter.

Les nombres relatifs (Z), ou simplement entiers, comprennent les nombres entiers naturels positifs et les nombres entiers négatifs.

Les nombres rationnels (Q) sont les fractions avec des nombre relatifs au numérateur et au dénominateur.

Les nombres réels (R) englobent les nombres rationnels (Q) et les nombres irrationnels.

Si un nombre irrationnel peut être défini par une équation*, il est algébrique, sinon, il est transcendant.

* Équation non nulle à coefficients rationnels.

Tous les nombres réels (R), sauf les transcendants, sont dits algébriques.

Les nombres complexes (C) sont formés d'un couple de nombres, l'un est réel (R), l'autre est imaginaire (I).

Relations

Un ENTIER	est	Rationnel
Un algébrique	est	Rationnel	ou	Irrationnel
Un TRANSCENDANT	est			Irrationnel

ALGÉBRIQUES réels

=

Rationnels

+

Irrationnels algébriques

RÉELS	=	Rationnels	+	Irrationnels
	=	Algébriques réels	+	Transcendants

Illustration

*Note: il existe aussi des nombres algébriques complexes

Voir TROIS TYPES de représentations de la classification des nombres

English

Natural numbers (N) are a subset of Integers.

Integers (Z) are a subset of Rational Numbers.

Rational Numbers (Q) are a subset of the Real Numbers.

Real Numbers (R) together with Imaginary Numbers (I) make up the Complex Numbers (C).

Dans Word, les fontes ajourées nommant les ensembles de nombres se trouvent en Insertion / Symboles /"Texte normal";

Voir aussi Segoe UI Symbol

Tableau des types de nombres (ensembles)

Nom	Définition
Entiers NATURELS	Nombres entiers naturels, abrégé en naturels. Vient de naturale (Peano). Ce sont les nombres de tous les jours. Ceux qui servent à compter. { 0, 1, 2, 3 … } { 1, 2, 3 … } N* représente l'ensemble des entiers privé du zéro. Suite >>>
Entiers RELATIFS	Nombres entiers relatifs, abrégé en entiers. Vient de Zahl, Zahlen, nombre (s) en allemand (Dedekind ou Georg Cantor). Le R étant réservé aux nombres réels. Avec les entiers naturels, on peut compter l'argent; en particulier, les gains. Il faut aussi pouvoir faire des calculs en prenant en compte les pertes. On peut le faire avec les nombres négatifs. Ensemble, les nombres entiers négatifs et les nombres entiers naturels (positifs), forment les entiers relatifs. { … -3, -2, -1, 0, 1, 2, 3 … } N est un sous-ensemble de Z. Suite >>>
Nombres DÉCIMAUX	Lorsqu'on mesure avec un mètre, ça ne tombe pas toujours juste; c'est même rare. Il faut utiliser des fractions d'unités: le décimètre ou le centimètre. On utilise alors les nombres à virgule. Les entiers sont aussi considérés comme des nombres avec une virgule, mais suivie de 0. Tous ces nombres sont des nombres décimaux. Exemples: 1 2 3,55 12,3456 Suite >>>

Nombres RATIONNELS	Nombres rationnels ou nombres fractionnaires Vient de quotiente, la fraction en italien (Peano) Il existe des nombres à virgule en plus de ceux qui servent à mesurer. Ce sont ceux des fractions telles que 1/3. Les chiffres derrière la virgule ne s'arrêtent jamais. Un motif se répète sans cesse. Les nombres entiers peuvent aussi se mettre sous la forme d'une fraction, avec un dénominateur à 1. Ces nombres à fraction (à ration !) sont appelé rationnels. Exemples: 1/3 = 0,333… 1/7 = 0,142857 142857 … Z est un sous-ensemble du corps Q. Suite >>>
Nombres IRRATIONNELS	Nombres irrationnels: tous les nombres qui ne sont pas rationnels, qui ne peuvent pas s'écrire sous la forme d'une fraction de nombres entiers. Suite >>>
Nombres ALGÉBRIQUES	Un nombre algébrique est solution d'une équation polynomiale non nulle à coefficients rationnels. Autrement-dit: il peut être défini par une expression plus ou moins compliquée. Par exemple, racine de deux est solution de l'équation x² – 2 = 0 (ou x² = 2). Les nombres algébriques sont tous les nombres réels ou complexes, sauf les transcendants. Suite >>>
Nombres TRANSCENDANTS (ou nombres non-algébriques)	Les nombres transcendants ne sont pas solutions d'une équation polynomiale à coefficients rationnels. Ce sont des nombres dont les chiffres derrière la virgule ne s'arrêtent jamais, mais ils ne se répètent jamais non plus. Parmi eux, on trouve des constantes mathématiques comme ou e, ou encore des nombres dont la puissance est irrationnelle comme: . Suite >>>
Nombres RÉELS	Nombres réels = algébriques + transcendants. Vient de real, réel (Dedekind). Tous les nombres, y compris cette nouvelle espèce, les nombres transcendants, forment l'ensemble des nombres réels. Exemples: 2 = 1 ,414 … = 3,14159… Q est un sous-ensemble du corps R. Suite >>>

Nombres IMAGINAIRES	Les nombres imaginaires résultent d'une façon d'imaginer ce que pourrait être la racine carrée d'un nombre négatif. Il est souvent commode d'effectuer des calculs avec ces nombre inventés et de ne conserver que les résultats réels en fin de calcul. Par définition et avec cette convention . En effet: Le nombre imaginaire est solution de l'équation x² + 1 = 0. L'ensemble des nombres imaginaires est noté . Suite >>>
Nombres COMPLEXES	Nombre complexe = couple formé par un nombre réel et un nombre imaginaire. Un bon moyen de se les représenter: ce sont les coordonnées a et b d’un point dans un plan sur des axes x et y. Par définition, a est la partie réelle et b est la partie imaginaire du nombre complexe. Exemples: 1 + i, 1 + 2i, -1,12 + 34,5, … R est un sous-ensemble du corps C Utilisés en électricité (i est alors noté j), en physique nucléaire, en aérodynamique, etc. Suite >>>
Nombres entiers de Gauss	Nombres Entiers de Gauss ou complexes entiers: a et b sont des nombres entiers. Ce sont des nombres complexes particuliers. Suite >>>
Nombres entiers d'Eisenstein	Nombres Entiers d'Eisenstein: N = a + w.b avec qui est un des racines de x^3 = 1. Suite >>>
Quaternions	Nombres hypercomplexes ou quaternions de Hamilton: généralisation des nombres complexes à quatre dimensions: quaternions L'ensemble des quaternions est noté . C est un sous-ensemble de H Utilisés en physique des particules et en robotique. Suite >>>
Octavions	Octavions (ou octaves ou octonions) de Cayley, nombres complexes à huit dimensions. Suite >>>
Nombres p-adiques	Nombres p-adiques: race de nombres, complétant les entiers rationnels d’une autre manière que ne le font les irrationnels pour donner les réels. Ils sont basés sur l’utilisation de développements infinis. Les mathématiques p-adiques occupent une position analogue aux géométries non-euclidiennes. Suite >>>

Propriétés		haut
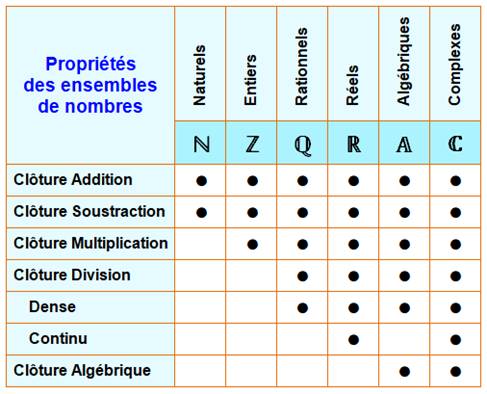
Clôture sous opérations: le résultat de l'opération est un nombre appartenant au même ensemble. Clôture algébrique: tout polynôme ayant des coefficients dans un ensemble a des racines dans cet ensemble. Dense: entre deux nombres de l'ensemble, il existe un autre nombre de l'ensemble. Continu ou complet: si une suite de nombres d'un ensemble converge, elle convergera vers un nombre de l'ensemble (suite de Cauchy).

Suite	Type de nombres – Index Inventaire – Graphe Découverte des nombres Écriture des nombres Groupes, anneaux, corps Nombre - Glossaire Nombres entiers Nombres premiers Presque-entiers Tous les noms des nombres
Voir	Calcul mental Crises en maths Décimalisation Dénombrable et continu Diagonale de Cantor Entier et formes polynomiale Fraction - Glossaire Géométrie Groupe Infinis des Jaïns Inverses et formes polynomiales Jeux Lambert Les nombres et leurs ensembles Liouville Nombre imaginaires Nombres périodiques Riemann Rubriques débutants Théorie des nombres Types de nombres selon leurs diviseurs
Nombres	Constante e Constante Pi Infini Racine de deux Zéro Zêta
Site	Ensembles de nombres – Wikipédia Ensembles de nombres – Maths-et-Tiques Les ensembles de nombres – Nicolas Durand Common Number Sets – Math is Fun Number – Wikipedia
Cette page	http://villemin.gerard.free.fr/Wwwgvmm/Type/Inventai.htm

Explication

Une explication déflore l'esprit de la blague, mais ici, je pense à tous ceux qui me lisent et qui ne sont pas mathématiciens. Il s'agit évidemment d'une blague absurde, voire stupide, de mathématicien.

Celui-ci ne raisonne pas en "êtres humains", mais en "êtres mathématiques". Ainsi un "être négatif" ne le gêne pas. Trois personnes sortant laisse donc la salle avec "moins une personne"; en faire entrer une nouvelle fera " + 1 – 1 = 0 = vide".

Retour

Renvois de liens

DÉFINITIONS NOMBRES ENTIERS >>>