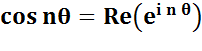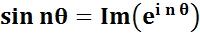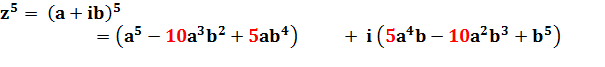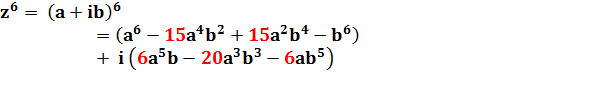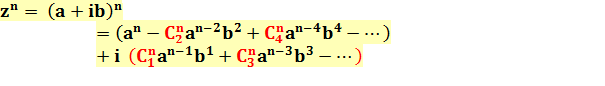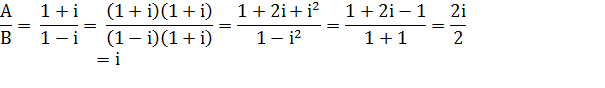|
||||||||||||||||||||||||||
![]()
|
PUISSANCE réelle d'un nombre complexe Développement du binôme
complexe. Quelques formules puis explication en deux temps. |
|
Ci-dessous,
explication du calcul de ces formules. |
|
|
|
|
La
première ligne se lit: (a + ib)2 = a2 + 2i ab + i2 b2 On
reconnaît naturellement le développement
du binôme. Dans
un premier temps, la valeur de in n'est
pas développée. Elle est indiquée en pied de tableau et va servir à calculer
le tableau final ci-dessous. |
|
|
|
|
|
Les
puissances de i ont été remplacées.
Par exemple: 120 i3 = -120 i. |
|
Voir Cas où ces
puissances produisent un nombre réel sans partie imaginaire
|
|
|
|
Calculs (exemple)
Note: la fraction inverse: B/A = – i >>> Voir Utilisation
du conjugué pour effectuer une division / Identités remarquables A² = (1 + i)²
= 1 + 2i + i² = 1 + 2i – 1 = 2i B² = (1 – i)²
= 1 – 2i + i² = 1 – 2i – 1 = –2i Tableau pour les
puissances n de 1 à 10
Illustration sur le
plan complexe
|
|
|
|
|
|
(1 + (1 +
|
|
![]()
|
Suite |
|
|
Voir |
|
|
Cette page |
http://villemin.gerard.free.fr/Wwwgvmm/Type/aaaCompl/PuisReel.htm |
![]()