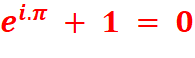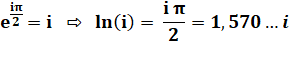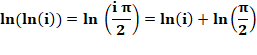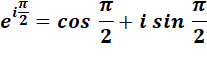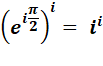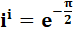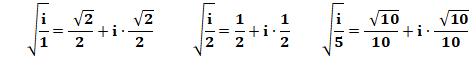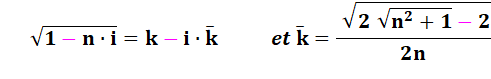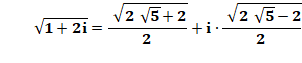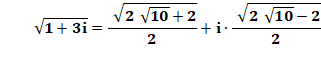NOMBRES – Curiosités, Théorie et Usages Accueil DicoNombre Rubriques Nouveautés Édition du: 30/05/2021 Orientation générale  DicoMot Math Atlas Actualités M'écrire Barre de recherche DicoCulture Index alphabétique Références Brèves de Maths
	Nombres complexes
Débutants Complexes	PUISSANCE			Glossaire Complexe
INDEX Complexes Puissances	Réelle	Imaginaire	Complexe	Multi-valeurs
		Sommaire de cette page >>> Puissance entière de i >>> Puissance complexe de i >>> Formule d'Euler >>> E puissance i Pi >>> Table des valeurs des puissances avec les imaginaires >>> Autres puissances avec i >>> Racine carrée de fractions de l'imaginaire >>> Racine carrée des multiples de l'imaginaire plus 1

Nombres complexes

PUISSANCE DE L'IMAGINAIRE

Généralement l'élévation à la puissance est à base d'entiers, voire de fractionnaires. Peut-on imaginer élever un nombre à une puissance imaginaire, voire un nombre imaginaire à une puissance imaginaire ? …

Que vaut i à la puissance i ?

Voir Calculs avec "i" / Racine carrée de – 1 et ses subtilités

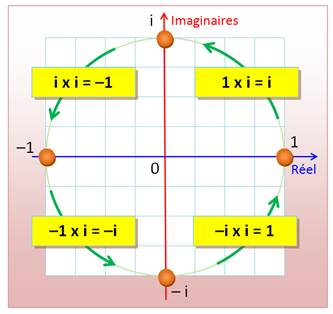
Puissance entière de i
En multipliant 1 par i, puis le résultat par i, on saute du monde imaginaire au monde réel, qu'ils soient positifs ou négatifs. Après quatre multiplications, on a fait un tour complet. i^2 = – 1 i^3 = – i i^4 = 1 Selon la puissance de i	Exemples i^100 = i^25 x4 = 1 i^101 = i^25 x4 +1 = i

Puissance complexe de i
Ce tableau se poursuit vers la droite avec une répétition modulo 4. Avec a = 4, on retrouve la colonne a = 0.

Voir Logarithme des complexes

Relations anglaises bien sympathiques

En français: i (imaginaire) 8 symbole de la somme pi

En anglais: aille eight sum pi

En lisant: I ate some pie (je mange un peu de tarte).

En lisant: I over ate (j'ai trop mangé).

Voir Pensées et Humour / Rébus

Formule et identité d'Euler
En 1748, Euler découvre la formidable identité. Cinq constantes fondamentales reliées entre-elles.
Une formule qui en découle:		Voir Calcul de la valeur de 1^infini
En fait, Euler découvrit plutôt la formule: En remplaçant x par Pi:
On a aussi: (valeur à 2Pi près)		Pour information sur le mode de calcul:
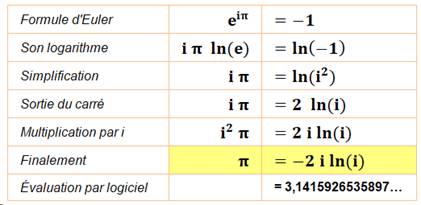
Valeur de Pi en imaginaire Patrick Even propose une bien belle façon de transformer la formule d'Euler. Elle donne à Pi une valeur avec les imaginaires.
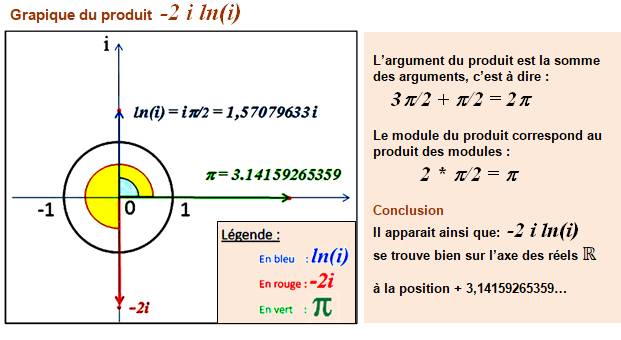
Patrick illustre la formule avec ce graphique. Voir cercle trigonométrique

Voir Exponentielle / Constante Pi et Euler / De Moivre / Trigonométrie / Logarithme de nombre négatifs

Approximation incluant le nombre d'or

E puissance i Pi
Un nombre irrationnel (Pi) à une puissance irrationnelle qui donne un nombre rationnel et même entier ! Et que pourrait donner un nombre imaginaire à une puissance imaginaire: un nombre réel!
Calculons avec Pi / 2. (formule d'Euler)
Élévation à la puissance i Avec De Moivre:	= 0,207 879 5 … Voir Multi-valeurs de i^i
= 0,2078795763 5076190854 6955619834 9787700338 7784163176 9608075135 8830554198 7728548213 9788600277 8654260353  (100 décimales). N'est-ce pas curieux de voir l'imaginaire à ce point puissant pour se reconvertir (renaître) en réel ?

Voir Constantes

Table des valeurs des puissances avec les imaginaires et leurs correspondances exponentielles

Les valeurs en i sont une des possibilités, car les fonctions exponentielles imaginaires sont multi-valeurs.

Voir Tables – Index

Quelques puissances avec au moins 3 décimales
Voir Exponentielles d'exponentielle Comment évoluent les puissances en étage

Voir Puissances à étages

Racines de l'imaginaire

Calcul de racine de i Prenons un nombre complexe dont le carré vaut i: (a + ib)² = i En développant: a² - b² + 2 iab = i (avec i² = -1) En égalant parties réelles: a² - b² = 0 et a = b En égalant parties imaginaires: 2iab = i et 2ab = 1 = 2a² Valeur de a et de b: a = racine de ½ = 0, 70710… Valeurs Illustration Prendre la racine carrée de i consiste à effectuer une rotation d'un demi-quart de tour dans le sens horaire.

Racine carrée de fractions de l'imaginaire

Formule générale

Exemples

Racine carrée des multiples de l'imaginaire plus 1

Formules générales

Exemples

Voir Nombres complexes conjugués

Suite	Puissance complexe Multi-valeurs des puissances complexes Complexes – Index
Voir	Constantes Construction de l'heptagone Inventaire des types de nombres Nombre de Gauss Nombres – Glossaire et index Nombres d'Eisenstein Nombres périodiques Nombres réels Puissances et racines – Index
Site	Complex exponentiation – Wolfram MathWorld
Cette page	http://villemin.gerard.free.fr/Wwwgvmm/Type/aaaCompl/PuisImag.htm