|
||||||||||||||||||||||||||||||||||||||||
![]()
|
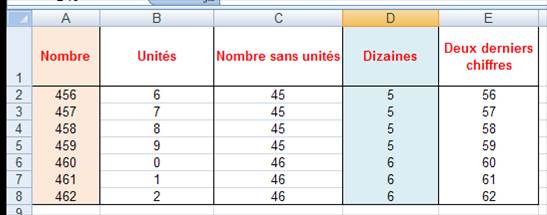
CHIFFRE des DIZAINES
23 comprend 2 dizaines
et 3 unités; 2 est le chiffre des dizaines. 153
comprend 15 dizaines et 3 unités; 5 est le chiffre des dizaines.
|
|
|
|
|
|
|
|
|
||
|
|
> for
N from 700 to 750 by 7 do QDiz:= iquo(N,10): Diz:= irem(QDiz,10): lprint (N,Diz): od: 700, 0 707, 0 714, 1 721, 2 728, 2 735, 3 742, 4 749, 4 |
|
Voir Programmation
de la division et ses applications
|
|
|||
|
Note: les
caractères liés à l'unité seulement sont donnés sur la page unité. |
|||
|
2 |
u = {0, 2, 4, 6, 8} |
1234 => 4 => 1234 divisible par 2 |
|
|
4 |
2d + u divisible par 4 |
556 => 2x5+6= 16 => 556 divisible par 4 |
|
|
5 |
u = {0,5} |
12345 => 5 => 12345 divisible par 5 |
|
|
10 |
u = 0 |
3210 => 0 => 3210 divisible par 10 |
|
|
20 |
ud ={00, 20, 40, 60, 80} |
1220 => 20 => divisible par 20 |
|
|
25 |
du = {00, 25, 50, 75} |
1050 => 50 => 1050 divisible par 25 |
|
|
50 |
du = {00, 50} |
1050 => 50 => 1050 divisible par 50 |
|
|
|
|||
|
|
|
|
N = … + 1000m + 100c + 10d
+ u N = 100 ( …10m + 1c) + 10d + u
(100 a + du)2
= (100 a + du)3
= (100 a + du)4
= (100 a + du)k
=
Si N = … DU Alors Nk = … du avec du dizaine et unité de DUk
|
|
|
k 34k 1234k 2 1156
1522756 3 39304
1879080904 4
1336336
2318785835536 5
45435424 2861381721051424 6
1544804416
3530945043777457216 7
52523350144
4357186184021382204544 8
1785793904896
5376767751082385640407296 9
60716992766464
6634931404835663880262603264 10
2064377754059776
8187505353567209228244052427776 |
|
|
|
|
|
Carrés
123476²
= 15 246 322 576 Cubes
1234763
= 1 882 554 926 394 176 Voir Unités et dizaines des
carrés et des cubes Puissances
4 (bicarrés)
1234764
= 232 450 352 091 447 275 776 Puissances
5
1234765
= 28 702 039 674 843 543 823 717 376 Puissances
6
1234766
= 3 544 013 050 890 981 417 177 326 718 976 Puissances
7
1234767
= 437 600 555 471 814 821 467 387 593 952 280 576 Puissances
8
1234768
= 54 033 166 187 437 806 895 507 150 550 851 796 402 176 Puissances
9
1234769
= 6 671 799 228 160 070 644 229
640 921 416 976 412 555 083 776 Puissances
10
127610
= 11 442 126 473 468 869 172 941
082 853 376 Ces nombres font partie de la catégorie des automorphiques. |
|
|
|
|
|
|
|
|
|
||||
|
Propriété des carrés
de certains nombres Les puissances
des nombres terminés par les nombres suivants se terminent toutes par ces
nombres, et il n'y en a pas d'autres.
Propriété de ces
nombres Les carrés
de ces sept nombres se terminent tous par le nombre lui-même. Dans l'ordre: 25, 625, 390625, 36, 5776, 141376, 87909376. |
Raison, par exemple
pour 76 Tout
nombre se terminant par 76 peut s'écrire 100A
+ 76 Exemple: 12376 = 123 x 100 + 76 Son carré devient: (100A + 76)² = 10000A² + 15200A + 5776 = 10000A² + 15200A + 5700
+ 76 = 100 (100A² + 152A + 57) + 76 =
100 B + 76 Le développement du carré redonne un nombre
du même type que le nombre initial; il se termine aussi par 76 et cela quels que
soit les autres chiffres placés devant; jusqu'à l'infini. |
|||
![]()
|
Suite |
|
|
DicoNombre |
|
|
Voir |
|
|
Cette page |
http://villemin.gerard.free.fr/aNombre/FORMATIO/Dizaines.htm |
![]()