|
||||||||||||||||||||||||||||||||||||||||||||||||||
![]()
|
Terminaisons des PRODUITS 1) On s'intéresse d'abord
aux unités de la table multiplication et de leur arrangement sur
le clavier de l'ordinateur. 2) Deux nombres se terminant
par une valeur donnée. Exemple de curiosité (ces nombres sont rares)
|
|
|
|
|
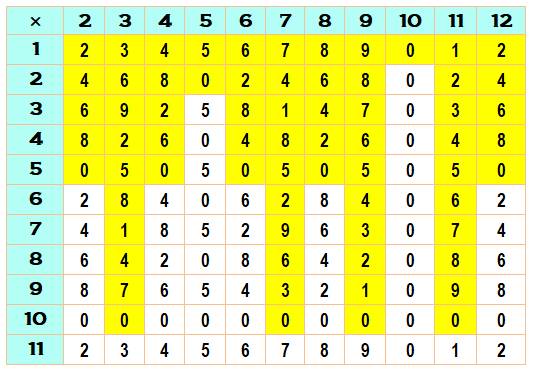
Unités des produits de la table de multiplication
jusqu'à 12
Position des unités successives sur le clavier
pour les tables du 2, du 3 et du 7
|
|
Voir Table
du 7 / Unités
des puissances
![]()
|
|
|||
|
Observations |
|
||
|
Table des
premières valeurs A et B se
terminent de la même manière. Est-il
possible de prédire la terminaison de leur produit ? Oui, dans les cas où, le nombre est
terminé par les chiffres suivants: |
|
||
|
|
||||
|
Unités Tableau => Dizaines La
première condition est que les unités se terminent de la même manière; soit: 0 , 1, 5, 6 Le
cas 0 est assez trivial (banal); on laisse tomber. 10 x 100 = 1 000 On
explore les 3 cas qui restent. Principe de
l'exploration Exemple ci-dessous
avec 25 |
|
|||
|
Deux nombres qui se terminent
par 25 |
A = 100a +
25 B = 100b +
25 |
A = 125 = 100x1 + 25 B = 725 = 100x7 + 25 |
||
|
Leur produit |
A.B
= (100a +
25)( 100b + 25) = 10 000ab +
2 500(a+b) + 625 |
A.B = 70 000 + 2 500 x 8 + 625 = 90
625 |
||
|
on note que |
10 000ab
aura toujours 4 zéros 2 500(a+b)
aura toujours 2 zéros |
70 000 +
20 000 +
00 625 |
||
|
Les deux chiffres restants sont ceux de |
625 soit 25 |
=
90 625 |
||
|
Le produit de
deux nombres terminés par 25 se termine par 25. Note: le produit se
termine par 625 si l'unité de 5(a + b) est égale à 0 |
||||
|
|
||||
|
On cherche une
terminaison k à 2 chiffres et se terminant par 1 telle que => |
...k x …k = …k |
|||
|
2 nombres
se terminant par k (à 2
chiffres): |
Ak = 100A + k Bk = 100B + k |
121 421 |
||
|
Leur
produit: Hors k²,
il se termine par 2 zéros. En
ajoutant k², Il se
termine par les deux derniers chiffres de k². |
Ak . Bk = (100A + k)(100B + k) = 10 000 AB + 100k (A+B)
+ k² |
121 x 421 = 10000(1 x 4) + 100 x 21 (1 + 4) + 21² = 40 000 + 10 500 + 441 = 50 941 |
||
|
Le produit de 2
nombres se terminant par k à 2
chiffres se termine par les 2 derniers chiffres de k² |
||||
|
Généralisation |
||||
|
Deux
nombres se terminant par k (à 3
chiffres): |
Ak = 1000A + k Bk = 1000B + k |
1234 5234 |
||
|
Leur
produit: Hors k²,
il y 3 zéros. |
Ak . Bk = (1000A + k)(1000B + k) = 1 000 000
AB + 1 000k (A+B) +
k² |
234² = 54 756 1234 x 5234 = 6 458 756 |
||
|
Le produit de 2
nombres se terminant par k à 3
chiffres se termine par les 3 derniers chiffres de k² Le produit de 2 nombres
se terminant par k à n
chiffres se termine par les n derniers chiffres de k² Le produit de Q
nombres se terminant par k à n
chiffres se termine par les n derniers chiffres de kQ |
||||
|
|
||||
Voir Multiplications
|
|
||||
|
On dispose
déjà de deux règles Explorons: |
Le chiffre des unités doit être: 1,
5 ou 6; Les deux chiffres sont les deux
derniers du carré. |
|||
|
Avec 1
|
Avec 5
|
Avec 6
|
||
|
Le produit de deux
nombres terminés par 25 se termine par 25 Le produit de deux
nombres terminés par 76 se termine par 76 Et ce sont les deux
seuls cas |
||||
|
|
|||
|
Le choix est limité car il faut que les
deux derniers chiffres soient identiques. Soit : 25 ou 76. |
Les deux
seules solutions
En fait, ces deux terminaisons donnent
chacune un filon. Q est la quantité de chiffres. |
||
|
25 Avec n
chiffres, les seules solutions
|
76 Avec n
chiffres, les seules solutions
|
||
|
Les mêmes avec
calcul sur 100 chiffres
Ces deux nombres N et M, au carré,
se terminent par eux-mêmes. C'est le cas aussi pour tous les
nombres formés à partir de ceux-ci en les tronquant à gauche, jusqu'aux
minimums que sont 5 et 6. |
|||
![]()
|
Même type
de sujets en |
|
|
Voir |
|
|
Cette page |
![]()