|
||||||||||||||||||||||||||||||||||||||||
![]()
|
CHIFFRE des UNITÉS
|
|
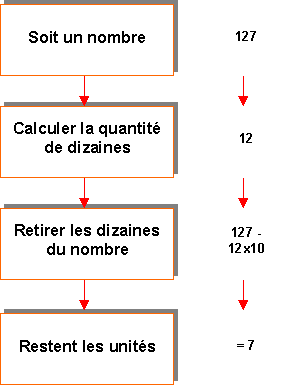
Considérez
les produits 1 x 2, 2 x 3, 3 x 4, etc. Ajoutez
les unités. Combien
de produits sont nécessaire pour avoir une somme égale à 100? |
|
|
|||||||||||||||||||||||||||
|
Pairs 0
2 4 6 8 Impairs 1 3 5 7 9
|
|||||||||||||||||||||||||||
|
Quels
sont les huit nombres égaux à un multiple
de leur unité? Il
en existe quatre avec les dizaines: 125
= 25 x 5 150
= 50 x 3 250
= 50 x 5 375
= 75 x 5 |
|
Programmation - (avec Mapple) for nombre from 110 to 125 do dizaines := trunc(nombre/10): unites
:= nombre - 10*dizaines: lprint (nombre,
dizaines, unites): od: Commentaires
Le travail à exécuter pour chaque valeur
explorée est encadré par do et od.
Autrement, il est possible d'obtenir tous
les résultats de calcul intermédiaires en mettant ";" au lieu des ":"
à la fin de chaque instruction. |
Exécution 110,
11, 0 111,
11, 1 112,
11, 2 113,
11, 3 114,
11, 4 115,
11, 5 116,
11, 6 117,
11, 7 118,
11, 8 119,
11, 9 120,
12, 0 121,
12, 1 122,
12, 2 123,
12, 3 124,
12, 4 125, 12, 5 |
Voir Extraction des chiffres d'un nombre / Algorithmes
/ Arrondis
|
|
||
|
N = … +
1000m + 100c + 10d + u N =
10 ( …100m + 10c + d) + u
(10a + u)2 = (10a + u)3 = (10a + u)4 = (10a + u)5 =
Si N = … U Alors Nk = … u avec u
unité de Uk
|
||
|
11² =
121 12² =
144 13² =
169 14² =
196 15² =
225 16² =
256 17² =
289 18² =
324 19² =
361 |
113 = 1331 123 = 1728 133 = 2197 143 = 2744 153 = 3375 163 = 4096 173 = 4913 183 = 5832 193 = 6859 |
|
Voir Unité et dizaines des
carrés
|
508 853 989 ² = 25 893 238 21 21 21 21 21 1 318 820 881 ² = 173 928 851 61 61 61 61 61 |
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
La puissance fait tourner la tête aux unités … Les
puissances n 1 2 3 4 5 6 7 8 9 10 n2 1 4 9 16 25 36 49 64 81 100 n3 1 8 27 64 125 216 343 512 729 1000 n4 1 16 81 256 625 1296 2401 4096 6561 10000 n5 1 32 243 1024 3125 7776 16807 32768 59049 100000 n6 1 64 729 4096 15625 46656 117649 262144 531441 1000000 n7 1 128 2187 16384 78125 279936 823543 2097152 4782969 10000000 n8 1 256 6561 65536 390625 1679616 5764801 16777216 43046721 100000000 n9 1 512 19683 262144 1953125 10077696 40353607 134217728 387420489 1000000000 n10 1 1024 59049 1048576 9765625 60466176 282475249 1073741824 3486784401 10000000000 Leurs
unités
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Voir Comment
trouver les derniers chiffres des puissances
|
|
|
|
Les nombres qui possèdent cette propriété
sont dits automorphiques.
Les
puissances 4k+1 d'un nombre reproduit son unité:
Voir les automorphiques à deux chiffres / Racine treizième |
|
|
|
|||
|
Premier cas |
|
|
|
|
Trouver la quantité
k de zéro et le chiffre u des
unités. |
420 x 565 |
= ….u000…0k |
|
|
Calcul sur les puissances: |
420 x 565 |
= 240 x 540 + 25 |
|
|
|
|
= 240 x 540 x 525 |
|
|
|
|
= 1040 x 525 |
|
|
Premier facteur: |
1040 |
1 suivi de 40 zéros |
|
|
Second facteur: |
525 |
= un nombre qui se termine par 5. (5 x 5 = 25; 25 x 5 = 125; …5 x 5 = …5) |
|
|
Solution: |
k u |
= 40 = 5 |
|
|
Nombre : 2 980 232 238 769 531 250 000 000
000 000 000 000 000 000 000 000 000 000 000 |
|||
|
Deuxième cas – Exposants inversés |
|
|
|
|
Trouver la quantité
k de zéro et le chiffre u des
unités |
465 x 520 |
= ….u000…0k |
|
|
Calcul sur les
puissances |
465 x 520 |
= 2130 x 520 |
|
|
|
|
= 2110+20 x 520 |
|
|
|
|
= 2110 x 220 x 520 |
|
|
|
|
= 1020 x 2110 |
|
|
Premier facteur |
1020 |
1 suivi de 20 zéros |
|
|
Second facteur |
2110 |
= 2110 = 24 x 27 + 2 Avec un reste de 2, la puissance de 2 se termine
par 4. |
|
|
Solution |
k u |
= 20 = 4 |
|
|
Nombre: 129 807 421 463 370 690 713 262 408
230 502 400 000 000 000 000 000 000 |
|||
|
Solution C'est un fait
remarquable: les unités des produits n (n + 1) sont en 2, 6, 2, 0 et 0, et
cela régulièrement. Tous les cinq
produits, la somme augmente de 10. Pour arriver à 100, il faut 50 produits.
Soit: 50 x 51. Pour être plus précis,
la somme ronde est atteinte avec le produit situé deux crans avant. Soit 48 x 49. Explication Forme générique d'un
nombre en isolant son chiffre des unités: 10d + u Produit: (10d + u)(10d + u +1) = 100d² + 20du + 10d + u² + u = 10(10d² + 2du + d) + u²
+ u Le chiffre des unités
du produit est celui de la somme: u² + u. Le tableau liste
toutes les valeurs possibles de u, de u² + u et de son chiffre des unités. |
|
![]()
|
Suite |
|
|
DicoNombre |
|
|
Voir |
|
|
Cette page |
![]()