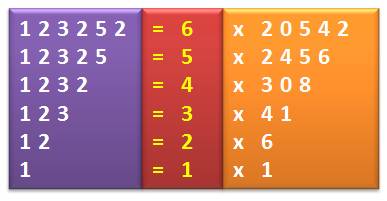|
||||||||||||||||||||||||||||||||
![]()
|
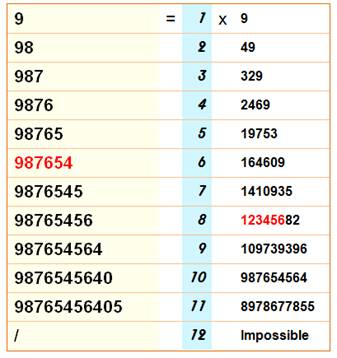
Nombres DIVISIBLES RÉSISTANTS Polydivisibles, Magiques, Persistants Nombres de n chiffres
divisibles par n, et restants divisibles en
éliminant ses chiffres les uns après les
autres. Exemple:
|
|
|
||||
|
Construire de tels nombres
n'est pas très difficile. Il suffit d'essayer les chiffres au fur et à mesure
en respectant les critères
de divisibilité. |
||||
|
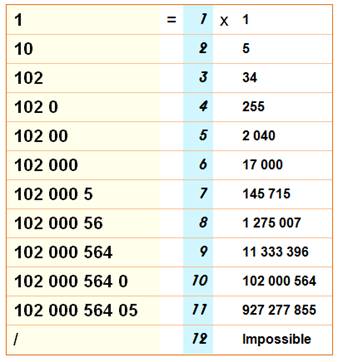
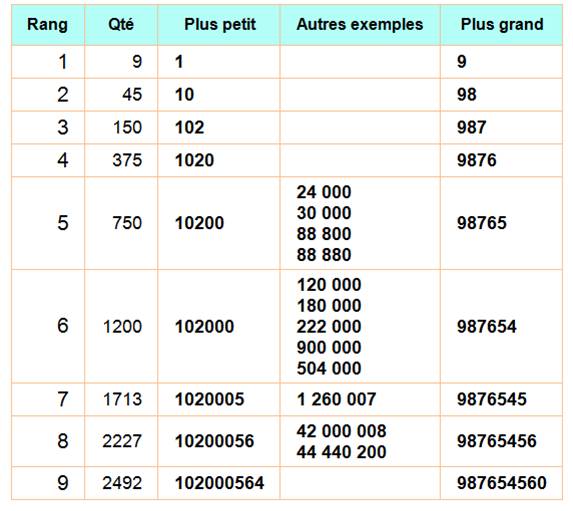
N° du chiffre |
Explications |
Qté |
Exemples |
|
|
1 |
Tous
les chiffres de 1 à 9 sont divisibles par 1. Il y en a 9. Le 0 en tête n'apporte rien. |
9 |
1, 2, 3 … |
|
|
2 |
Tous les
nombres pairs à deux chiffres sont divisibles par 2. Ils sont 5 par dizaine, soit 9 x 5 = 45. |
45 |
10, 12, 14 … |
|
|
3 |
Avec
trois chiffres, le 3e chiffre, ajouté aux deux autres doit donner
un nombre divisible par 3. Ils sont 3 ou 4 selon la dizaine: 10 (2, 5, 8); 12 (0, 3, 6, 9); 14
(1, 4, 7); 16 (2,,5, 8) … |
150 |
102, 120, 141 … |
|
|
4 |
Il
suffit que les deux derniers chiffres forment un nombre divisible par 4. |
375 |
1020, 1200, 1412 … |
|
|
5 |
Ajoutez
un 0 ou un 1. |
750 |
10200, 12000, 14120 … |
|
|
6 |
Cela
devient un peu plus fastidieux. Le nouveau nombre doit être pair et divisible
par 3. |
1200 |
102000, 120000, 141204 … |
|
|
7 |
Là, ça
se complique! |
1713 |
1020005, 1200003, 1412040 … |
|
|
8 |
Sans ordinateur,
difficile; à la limite avec un tableur |
2227 |
10200056, 12000032, 14120400 … |
|
|
9 |
Jusqu'ici,
on trouve toujours un nouveau chiffre à ajouter tout en conservant la
divisibilité. Parmi les dix nouveaux nombres qu'il est possible de former, il y en a
toujours un divisible par un nombre inférieur à 10. |
2492 |
102000564, 120000321, 141204006 … |
|
|
10 |
Avec
un zéro de plus, le tour est joué. Et c'est la limite pour laquelle il ne sera pas toujours possible
d'obtenir un nombre divisible plus grand. |
2492 |
1020005640, 1200003210, 1412040060 … |
|
|
|
|
|
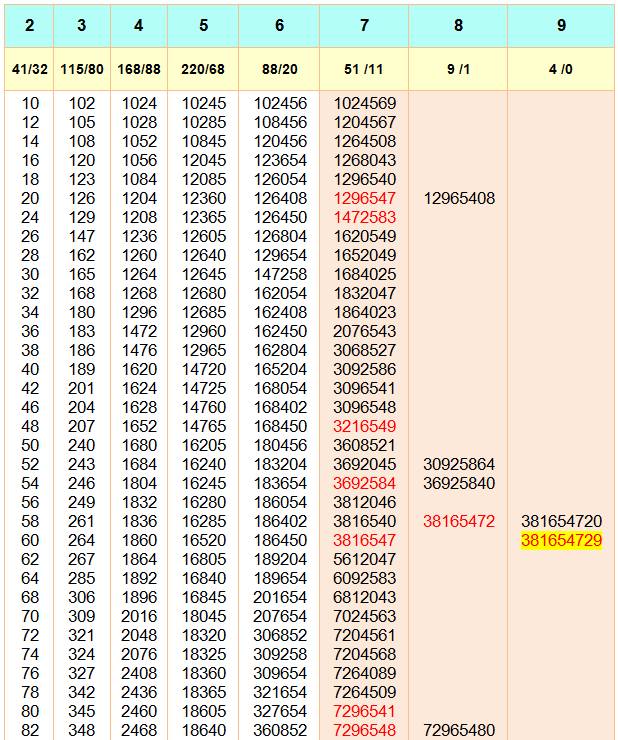
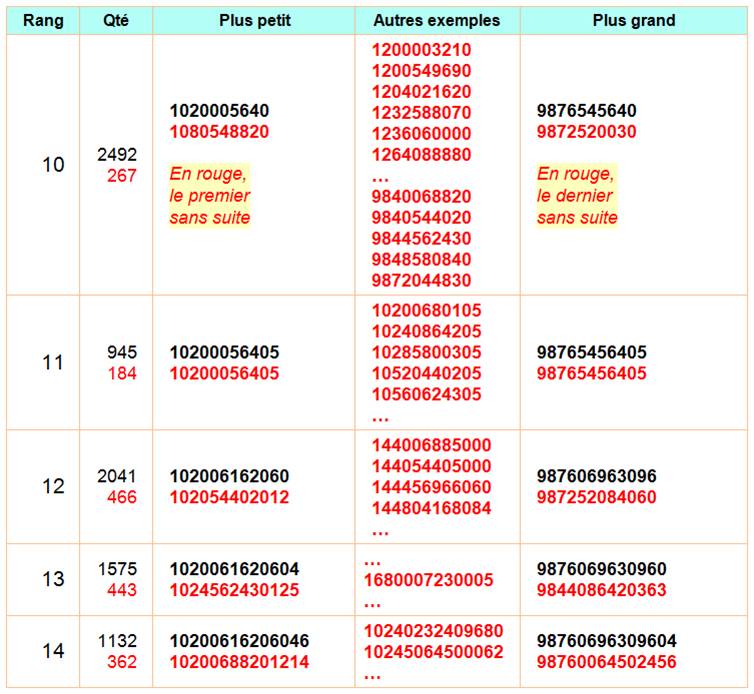
Nous nous intéressons aux
nombres dont tous les chiffres sont différents. Tous ces nombres sont
divisibles résistants et, donc, à 2, 3, … 9 chiffres différents. Ligne jaune: quantité de
nombres en incluant le zéro / sans zéro. En ocre, à droite, tous les nombres pour 7, 8 et 9 chiffres et,
parmi eux, en rouge ceux sans 0. Un seul élu pannumérique complet sans le 0:
381 654 729,
ou a dix chiffres en lui ajoutant le 0 en unité. Voir Ce nombre
est unique – Démonstration Notez bien qu'il existe 41 nombres à deux chiffres et non 45
comme indiqué ci-dessus car les nombres 22, 44, 66 et 88 sont éliminés, ici.
Il n'y en a plus que 32 si on retire ceux comportant un 0.
|
|
|
|
||
|
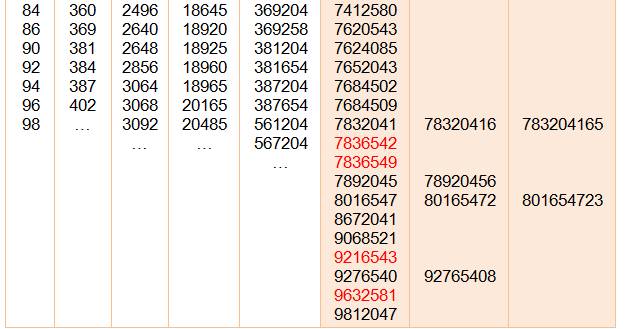
En ajoutant un nouveau
chiffre, le nouveau nombre n'est jamais divisible par 12.
Le plus grand est un nombre
à vingt-cinq chiffres. Le voici: 0,3608
...1025 |
|
|
|
Le plus grand divisible résistant et ses 25
chiffres
|
||
|
|
|
|
Par
contre: 1080548820 n'est jamais divisible par
11 quel que soit le chiffre ajouté. C'est un résistant! Le plus petit nombre divisible
résistant. |
|
Suite de
la table de 10 à 25 chiffres


|
Les
nombres divisibles résistants sont en nombre fini. Le dernier s'écrit avec 25
chiffres. Tous ses nombres tronqués d'un chiffre par la droite sont divisibles
par la quantité de chiffres de ce nombre tronqué.
Exemple: en
enlevant le 5 à droite: 360 852 885 036 840 078 603 672
/ 24 = 15 035 536 876 535 003 275 153. |
Voir Polydivisible
![]()
|
Suite |
|
|
Voir |
|
|
DicoNombre |
|
|
Cette page |
http://villemin.gerard.free.fr/aNombre/MOTIF/Chiffres/PerDivis.htm |
![]()