|
||||||||||||||||||||||||||||||||||||||||
![]()
|
Nombres premiers RÉSISTANTS Tronquables Effaçables Nombre
qui reste premier en lui supprimant ses chiffres les
uns après les autres. Record par la droite: 73 939 133 – Ils sont 83. Record par la gauche: 357 686 312 646 216
567 629 137 – Ils sont 260. |
Anglais: Truncatable prime
Premiers ambidextres ou recto-verso ou des deux côtés
|
Il
existe 15 nombres à la fois résistants à gauche comme à droite. 2, 3, 5, 7, 23, 37, 53, 73, 313,
317, 373, 797, 3 137, 3 797, 739 397. |
Anglais: Two-sided troncatable primes
|
|
||
|
|
73 939
133 73 939
13 73 939
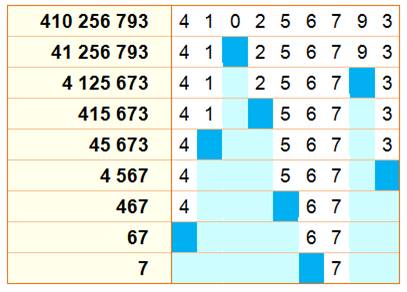
1 73 939 73 93 73 9 73 7 Ces nombres, obtenus par effacement du chiffre de droite, restent
premiers |
|
|
Graphe des 83 nombres
premiers résistants
par la droite |
|
|
|
|
Autre
présentation en y incluant le 1 initial (par exception)

|
|
|||||||||||
|
|
33 333
331 3 333 331 333 331 33 331 3 331 331 31 |
||||||||||
|
|
632 647 32 647 2 647 647 47 7 |
||||||||||
|
Les plus grands à N chiffres => |
8 chiffres: 99 979 337 9 999 962 683 10 9 987
983 617 |
||||||||||
|
Spécimen trouvé par Chris Caldwell Suite >>> |
357
686 312 646 216 567 629 137 57
686 312 646 216 567 629 137 7
686 312 646 216 567 629 137 … |
||||||||||
|
|
Sans autoriser le
0, Il y en a 4 260. |
||||||||||
|
Quantité selon le nombre de chiffres, ci-dessous: |
|||||||||||
|
1 4 |
2 +11 |
3 +39 |
4 +99 |
5 +192 |
6 +326 |
7 +492 |
8 +521 |
9 +545 |
10 +517 |
||
Voir Table des résistants par la gauche en
…11
|
|
|
|
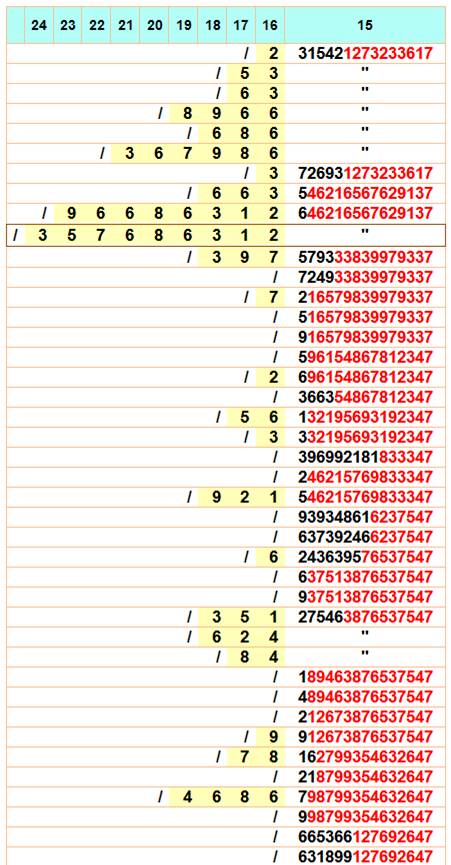
Les quatre records
Record en 7 Le record avec cette séquence
est un nombre à 24 chiffres. Chaque fois qu'un nombre est supprimé par la
gauche, il reste premier. 357 686 312 646 216
567 629 137 Le tableau suivant montre sa
genèse; toutes les possibilités offertes aux nombres à partir de 14 chiffres
de devenir ce nombre record. Tous les nombres de ce tableau sont premiers
résistants à gauche. Ils sont 97 candidats avec 15 chiffres. Le record se
trouve en 10e position (encadré). Le tableau montre que la famille
est riche en longs résistants à gauche. Lecture du tableau Le nombre de 15 chiffres
(ligne 1 à droite) est premier résistant à gauche et, il le reste en lui
ajoutant 2, mais pas plus (/); il le reste en ajoutant 53 ou 63, mais pas
plus; il le reste en ajoutant 8966; etc. En rouge, la partie du nombre
commune avec l'un de ses deux voisins. Tableau des grands nombres
résistants à gauche formés à partir de 7
|
|
|
par
le milieu et palindrome |
|
|||
|
Pyramides de premiers palindromes. Les six seules pyramides existantes. |
||||
|
2 9 2 9 39 2 93 739 2 937 3739 2 9373 |
2 9 2 9 39 2 93 339 2 933 7339 2 9337 |
3 1 3 1 11 3 11 |
3 1 3 1 71 3 17 |
|
|
5 1 5 1 31 5 13 331 5 133 |
5 3 5 3 33 5 33 133 5 331 |
5 7 5 7 37 5 73 937 5 739 |
7 3 7 3 93 7 39 |
|
Voir Sites
|
ou
premiers effaçables |
|
|
|
|
|
|
||
|
Trouvé par L.
Nelson. |
1 023 456 987 896 543 201 |
|
|
|
|
|
|
|
Voir Integer sequence A024770 et
![]()
|
Nombre premier tronquables |
|
|
|
Programme Maxima
|
Commentaire Ce
programme prend comme racine les nombres premiers à un chiffre, puis ajoute progressivement
des chiffres à droite tout en ne conservant que les nombres premiers. Aucune
astuce de programmation : on forme la liste des nombres premiers à deux
chiffres, puis trois, puis quatre, etc. Le
résultat du traitement est indiqué ci-dessous. Maximum :
cinq nombres premiers de huit chiffres tronquables à gauche. |
|
Voir Programmation – Index
|
Liste des nombres premiers tronquables à droite [23, 29, 31, 37, 53, 59, 71, 73, 79] 9 [233, 239, 293, 311, 313, 317, 373, 379, 593, 599, 719, 733, 739, 797]
14 [2333, 2339, 2393, 2399, 2939, 3119, 3137, 3733, 3739, 3793, 3797,
5939, 7193, 7331, 7333, 7393] 16 [23333, 23339, 23399, 23993, 29399, 31193, 31379, 37337, 37339, 37397,
59393, 59399, 71933, 73331, 73939] 15 [233993, 239933, 293999, 373379, 373393, 593933, 593993, 719333,
739391, 739393, 739397, 739399] 12 [2339933, 2399333, 2939999, 3733799, 5939333, 7393913, 7393931,
7393933] 8 [23399339, 29399999, 37337999, 59393339, 73939133] 5 [] 0 Liste des nombres premiers tronquables à gauche [13, 23, 43, 53, 73, 83, 17, 37, 47, 67, 97] 11 [113, 313, 613, 223, 523, 823, 443, 643, 743, 353, 653, 853, 953, 173,
373, 673, 773, 283, 383, 683, 883, 983, 317, 617, 137, 337, 937, 347, 547,
647, 947, 167, 367, 467, 967, 197, 397, 797, 997] 39 [2113, 5113, 6113, 3313, 1613, 3613, 9613, 1223, 1523, 4523, 7523,
1823, 3823, 6823, 7823, 5443, 8443, 3643, 4643, 7643, 9643, 5743, 9743, 6353,
8353, 5653, 6653, 3853, 7853, 2953, 5953, 6173, 9173, 1373, 3373, 4373, 6373,
3673, 4673, 6673, 7673, 1283, 4283, 7283, 9283, 2383, 2683, 5683, 6883, 7883,
9883, 6983, 6317, 8317, 2617, 3617, 2137, 3137, 9137, 4337, 6337, 9337, 4937,
7937, 2347, 3347, 5347, 3547, 4547, 6547, 7547, 9547, 2647, 5647, 8647, 3947,
6947, 3167, 5167, 8167, 1367, 6367, 2467, 3467, 8467, 9467, 3967, 4967, 6967,
9967, 5197, 6197, 4397, 6397, 9397, 2797, 3797, 1997, 6997] 99 Etc. Ils sont très nombreux à 5,
6, 7, 8 et 9 chiffres : 192, 326, 429, 521, 545. Le plus grand à neuf chiffres est : 999 636 997 |
![]()
|
Voir |
|
|
Voisins |
|
|
DicoNombre |
|
|
|
|
|
Sites OEIS |
|
|
Cette page |
![]()