|
|
Approche |
|
|
|
Définition |
Homothétie: un point O
du plan et k un réel, on
appelle homothétie de centre O
et de rapport k, la
transformation qui à tout point M
du plan associe le point M’
tel que |
|
![]()
|
Types |
Avec k
> 1, l’homothétie est un agrandissement
(zoom-avant); Avec k =
1, l’homothétie est l’identité I
(lettre grand I); Avec k
< 1, l’homothétie est une réduction
(zoom-arrière); Avec k = - 1, l’homothétie est la rotation de centre O et d’angle Voir Symétrie |
|
Propriétés |
|
![]()
|
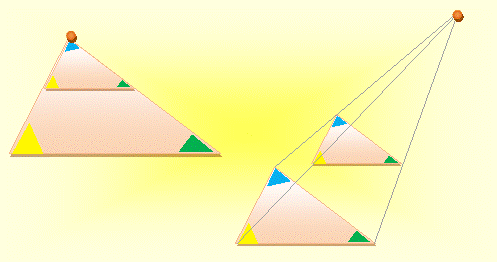
Similitude et homothétie |
Triangle origine
Similitude directe Similitude
indirecte
Homothétie avec centre sur la figure (simple grossissement) Homothétie
avec centre hors de la figure
|
![]()
|
|
|
|
Famille |
Application
Voir Théorème
de Thalès, similitude |
![]()
Exemple d'application avec le
théorème de Pythagore
|
Démonstration visuelle de l'inverse du théorème
de Pythagore Triangle
rectangle du haut: le cas classique du théorème
de Pythagore. Toutes les mesures sont divisées par ab pour
obtenir le triangle rectangle du bas. Le théorème de Pythagore s'applique aux nouvelles
mesures. La relation
ah = bc qui donne h en fonction de a, b et c dans le triangle rectangle
complète l'égalité. |
Deux triangles semblables dans un rapport 1/ab
|
Voir Démonstration
de l'inverse du théorème de Pythagore
|
Anglais |
Dilatation: a dilatation of the plane from O with scale factor
c (c This is given in terms of Cartesian coordinates by Note: attention au sens de dilatation
en français |
|
En savoir plus |
|
|
Sites |
|