|
|||||||||||||||||||||||||||||||||||
![]()
|
SAUTS
de la GRENOUILLE Où la grenouille rejoint les lapins |
|
|
|
|
Nénuphars Une grenouille
saute sur des nénuphars.
Échelle On pose parfois
le problème de la grenouille avec une échelle |
|
|
|
||||||||||||||||
|
La grenouille
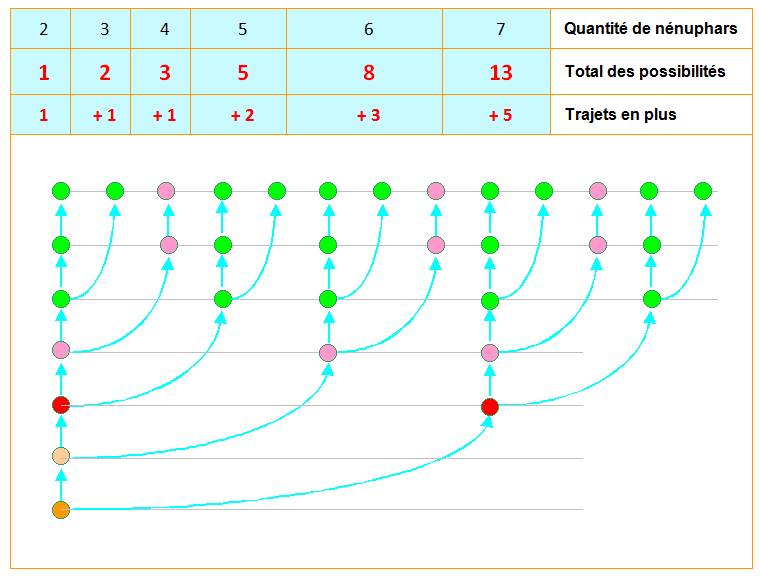
commence par 2 puis 3 ou 4 nénuphars
pour s'entraîner Voici les
trajets possibles Sur l'illustration,
on développe tous les trajets possibles:
Remarque très
importante Notons
Tn la quantité totale de trajets possibles pour n nénuphars
|
||||||||||||||||
|
|
|
|
Avec
un peu de méthode, la grenouille peut se lancer sur la prairie des nénuphars
|
|
|
|
|||||||||||||||||||||||||||||||
|
Principe du
calcul On fait le compte
pour 2 puis 3 puis 4 … nénuphars On remarque que
pour 4 nénuphars (T4), il y deux cas:
la grenouille
fait un saut de 1 nénuphar et se retrouve
comme elle l'était avec 3 nénuphars: T3
la grenouille
fait un saut de 2 nénuphars et se retrouve
comme elle l'était avec 2 nénuphars: T2 T4 = T3 + T2 Cette propriété
se vérifie toujours Tn = Tn-1
+ Tn-2 Or, on sait que T2 = 1 T3 = 2 Il suffit
maintenant de faire les comptes successifs: T4 = T3 + T2 = 2 + 1 = 3 T5 = T4 + T3 = 3 + 2 = 5 … Valeurs
|
|||||||||||||||||||||||||||||||
|
|
|||||||||||
|
Suite de Fibonacci
Lapins de
Fibonacci
|
|||||||||||
![]()