|
||||||||||||||||||||||||||||||||||||
![]()
|
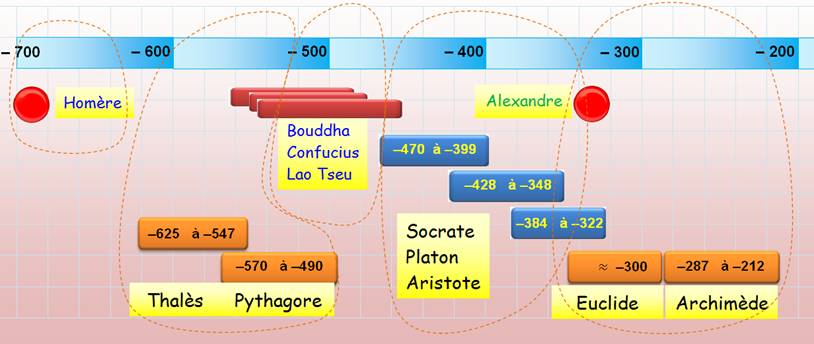
CHRONOLOGIE des années Av. J.-C. Historique
des mathématiques de l'Antiquité. Comment
tout cela a-t-il commencé ? Il est stupéfiant de réaliser combien les
sciences étaient déjà bien avancées avant notre ère. Un mérite d'autant plus
important pour ces savants qu'ils ne disposaient pas des outils les plus
simples à notre disposition aujourd'hui. Ne serait-ce que le papier à
volonté, le système décimal, les notations ou encore les bibliothèques. Certains d'entre eux sont devenus très
célèbres par leurs œuvres. Il ne faut pas oublier tous les autres chez qui
ceux-là ont pioché leur inspiration.
Cette chronologie tente de redonner crédit à ces quelque peu oubliés. Les plus vieux témoins 3000 millions d'années: preuve
fossile de photosynthèse et production d'oxygène; cyanobactéries*; 400 millions d'années: apparition
des végétaux (racines, tiges et feuilles); 75 millions d'années: le plus vieux
dinosaure découvert; 700 000 ans: les plus vieux
mammifères découverts (fémur de cheval au Canada); 430 000 ans: les plus vieux humains
découverts (Homo heidelbergensis). Repères Il y a 2 500 ans, dans le Grèce
antique, le philosophe Pythagore crée une école autour de l'étude des
nombres; Il y a 2 500 ans, les Babyloniens
utilisent le zéro pour former les grands nombres; Il y a 2 200 ans,
dans le Grèce antique, les soldats échangent des messages codés à l'aide de
scytales. |
* Source:
Timeline of
plant evolution – Wikipedia – Avec
schémas chronologiques
|
|
|
|
Formation
de l'Univers
Apparition
du vivant jusqu'à l'homme
Note: 1,8
milliard ne
prend pas de "s" Voir Les huit
seuils de l'histoire de l'Univers / Aires géologiques
Traditionnellement l'Antiquité commence
avec l'avènement de l'écriture qui termine la préhistoire. Elle finit en 476 à la chute
de l'Empire romain d'Occident, lorsque commence le Moyen Âge.
|
|
|
Les grands savants connus de l'Antiquité
|
|
|
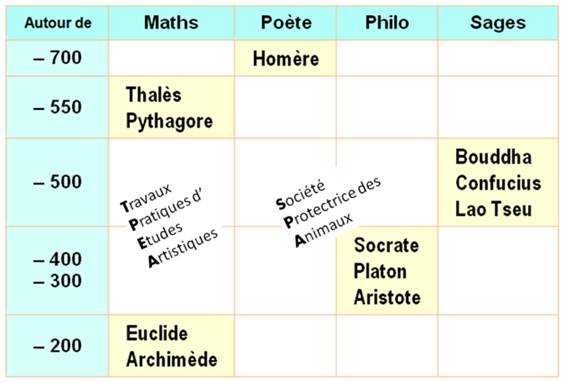
Mémorisation
de ce tableau
Notez les
deux acrostiches mnémotechniques. |
|
![]()
Chronologie détaillée
|
|
|||
|
– 20 000 |
Préhistoire |
Des entailles dans le bois
représentent les nombres. L'os d'Ishango (Congo) serait
la plus ancienne manifestation mathématique: bâton de comptage ou
identification des nombres premiers (5, 7, 11, 13, 17, 19)? |
|
|
– 15 000 |
Dessins |
Dessins des grottes de
Lascaux |
|
|
– 4 500 |
Sumer (confluence du Tigre et de l'Euphrate) |
Apparition des
opérations sur des tablettes d'argile (multiplication et division) en Mésopotamie. Au vu des objets fabriqués, on suppose que les vieux
royaumes de l'Égypte et de l'Indus avaient déjà développé des aptitudes
arithmétiques. |
|
|
– 4 000 |
Antiquité |
Apparition de l'écriture;
date conventionnelle du passage de la préhistoire à l'Antiquité (en 3 300 av.
J.-C. pour les Mésopotamiens). |
|
|
– 3 500 |
Sumer |
Connaissance des carrés, cubes et même logarithmes. Numération
de position en base 60. Les nombres sont basés sur la valeur des chiffres
selon leur position. Invention d'un zéro
de position, mais ne le considèrent pas comme un chiffre. Il n’a pas de zéro, ou plutôt c’est l’espace vide au
milieu d’un nombre, mais pas possible aux extrémités. On différencie 102 et
12, mais pas 12 et 120. |
|
|
– 3 000 – 2 000 |
|
Mesures topologiques. Solution de certaines équations du 2e degré. Utilisation des nombres
négatifs. Notion de trigonométrie (en fait,
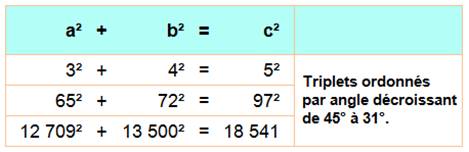
triplets de Pythagore) On voit dans cette tablette (Plimpton 322)
et dans d’autres que les scribes babyloniens maîtrisaient parfaitement les
principes de la propriété de Pythagore. Ils ont
des procédures qui montrent qu’ils sont absolument sûrs de la validité de
cette relation. C’est clair que Pythagore ne fut pas le premier! Depuis les
années 1940, on sait qu’en Mésopotamie, ils avaient des pratiques
mathématiques très élaborées, très sophistiquées et qui, par certains égards,
dépassent celles des Grecs. Ils ont aussi une parfaite maîtrise de la
propriété de Thalès, qui permet les agrandissements et les réductions de
figures. Ils étaient des virtuoses de ce qu’on appelle les homothéties. Christine Proust –
Chercheuse au CNRS – 2017 Voir
Tablette
Plimpton / Théorème
de Pythagore / Théorème de
Thalès |
|
|
– 2 500 |
Pyramide |
Construction des pyramides de Khéops, Khéphren et Mykérinos
démontrant des aptitudes à la géométrie. |
|
|
– 1 900 –
1 600 |
Babylone |
Tablette de Plimpton 322 découverte
en 1945 par O. Neugebauer & A. Sachs. Invention probable du boulier. Ils donnent
la valeur de Triplets de
Pythagore, 1000 ans avant Pythagore. |
|
|
– 2 000 |
Bible |
Abraham / -1200 Mose / -1000 David. |
|
|
– 2 000 |
Papyrus de Moscou |
Il contient 25
problèmes avec solutions comme le calcul de la surface d'une demi-sphère ou du volume d'une pyramide tronquée. |
|
|
– 1 550 |
Papyrus Rhind |
Écrit par le scribe Ahmès, il
contient 87 problèmes d'algèbre, de géométrie et d'arpentage avec les
solutions. Usage des fractions égyptiennes. |
|
|
– 2 000 –
1 700 |
Égyptiens |
Les Égyptiens
utilisent la géométrie pour résoudre des problèmes pratiques. A'hmosé (Égyptien)
décrit des méthodes pour résoudre des problèmes mathématiques : un des
plus anciens documents connus. |
|
|
/ |
Chinois Indien |
On ne connaît rien de plus qu'en
Mésopotamie. En tout cas
rien qui a marqué la suite de l'histoire de la théorie des nombres. |
|
|
– 1 300 |
Lagadha |
Indien astronome, utilisant la
géométrie et une trigonométrie rudimentaire. |
|
|
– 1 250 |
Troie |
Guerre de Troie. |
|
|
/ |
Grecs |
Les Grecs vont faire la
Une. Ils
introduisent les outils que nous connaissons aujourd'hui: Déduction,
preuves, théorèmes, abstraction. Les Grecs
utilisent le boulier, première machine à calculer vers -500 |
|
|
– 1 200 |
Alphabet |
Phénicien (Liban actuel). |
|
|
– 1 200 |
Chine |
Premier système décimal de position
connu. |
|
|
– 1 200 |
Inde |
Mantras védiques: énonce les
puissances de 10 jusqu'à 1012. |
|
|
– 931 |
Salomon |
Fils et successeur du roi David, roi
d'Israël Réputé pour
sa sagesse. |
|
|
– 800 |
Grèce |
Naissance des cités grecques. |
|
|
– 800 |
Yajnavalkya |
Meilleure approximation de Pi à cette époque. |
|
|
– 740 |
Baudhayana |
Mathématicien indien: traité
d'algèbre et de géométrie. Calculs pour
la construction d'autels. Plusieurs
approximations de Pi et de racine de 2. |
|
|
– 750 |
Social |
Démocratie athénienne. |
|
|
|
Manava Sulbasutra |
Calculs de constructions. Approximation
de Pi et de racine de 2. Nombreux triplets de Pythagore. |
|
|
– 753 |
Rome |
Fondation de Rome. |
|
Autres avant l'an -1000
|
D'autres peuples avaient sans doute développé des connaissances mathématiques.
Pour information; les Incas occupaient la
bande côtière ouest de l'Amérique du sud: Équateur, Pérou et Bolivie |
|
VIIe siècle av. J.-C. (– 700 à – 601) |
Physiciens
de Milet: Thalès, Anaximandre,
Anaximène: Étude de la nature. |
||
|
VIe siècle av. J.-C. (– 600 à – 501) |
École
d'Elée: Xénophane de Colophon, Parménide, Zénon, Mélissos: Unité |
||
|
|
Poète: l’Iliade et l’Odyssée lui
sont attribuées. Voir Ulysse / Pénélope |
||
|
|
Lo Shu |
Carré magique d'ordre 3. |
|
|
– 560 |
APASTAMBHA |
Mathématicien indien (védique) Techniques de mesure, construction
géométriques, algèbre élémentaire Première preuve (sans doute) du théorème de Pythagore. Approximation de |
|
|
|
Monnaie |
métallique en Lydie (Asie Mineure). |
|
|
– 551 |
Zarathoustra |
Prophète religieux perse. |
|
|
– 625 – 547 (78 ans) |
de Milet |
L'un
des sept sages (et le plus
connu aujourd'hui). Premier
penseur et premier mathématicien de l'Histoire. Il
utilise pour la première fois les démonstrations déductives. Il ramène des
connaissances de Babylone et d’Égypte. Théorème de Thalès: AB/AC =
A’B’/A’C’. Scientifique: Eau: premier élément
qui donne naissance aux autres; Célèbre pour avoir prévu une éclipse (585); Observe l’attraction du fer
par certains minerais de fer. |
|
|
– 610 – 546 (64 ans) |
ANAXIMANDRE |
Philosophe,
mathématicien, astronome grec adepte de l'expérimentation. Invente
la cartographie. Introduit
le cadran solaire en Grèce. Succède
à Thalès, et Pythagore est un de ses élèves. |
|
|
|
|||
|
VIe siècle av. J.-C. (– 600 à - 501) |
Pythagoriciens
de Croton, Pythagore de Samos: Nombres,
arithmétique, duplication du carré, science en général |
||
|
Ve siècle av. J.-C. (– 500 à - 401) |
École de Chios:
Œnopide, Hippocrate: Quadrature du
cercle, duplication du cube, trisection de l'angle >>> Sophistes
et Mégariques: Hippias d'Elis, Euclide de Mégare: Quadratrice. Atomistes
d'Abdère: Leucippe, Démocrite: Premier
algorithme infinitésimal, notion
d'atomes >>> |
||
|
– 570 – 490 (80 ans) |
Né à Samos. élève d'Anaximandre. Voyage
en Babylone, Égypte et Inde (sans doute). Il
fonde une confrérie basée sur les mathématiques: association scientifique,
philosophique, politique et religieuse. Premier à
utiliser des axiomes et un raisonnement déductif. Idéalise
les nombres entiers. Il découvre
que la musique est liée aux nombres rationnels. Théorème de Pythagore. / Décade
de Pythagore En
astronomie, le premier à réaliser que la Terre
est une sphère comme les autres planètes. École
de Pythagore: Parménide d'Élée, Hippase de Métaponte, Alcméon de Crotone
(anatomiste), Milon de Crotone (athlète). Une des rares école à pratiquer
l'égalité des sexes. |
||
|
– 483 (80 ans) |
BOUDDHA Siddharta
Gautama |
Sage indien né dans l'actuel Népal. Parvenu à l'éveil (bodhi). Bouddhisme. |
|
|
– 551 – 479 (72 ans) |
CONFUCIUS |
Philosophe chinois. Grande figure de
la civilisation chinoise. |
|
|
– 450 |
LAO TSEU |
Philosophe taoïste chinois, sans
doute un peu plus âgé que Confucius. |
|
|
– 590 |
ÉPIMÉNIDE le Crétois |
Sa phrase célèbre: tous les Crétois
sont des menteurs. >>> |
|
|
– 520 – 460 (60 ans) |
PANINI de Shalatula |
Premier grammairien et linguiste indien
(sanskrit). Surnommé le Euclide indien du fait
de sa rigueur. Il a sans doute inspiré le
développement de l'algèbre et des sciences en Inde. |
|
|
– 515 – 460 (55 ans) |
PARMÉNIDE d'Élée |
Philosophe de
l'école de Pythagore. Sans doute, auteur de certaines
idées attribuées à Pythagore. Prétendait que le néant ne pouvait
exister, parce que parler de quelque chose le fait, de facto, exister >>> |
|
|
|
HIPPASE de Métaponte |
Pythagoricien. Il Invente la moyenne harmonique. Créditée de la découverte des irrationnels et puni de noyade pour avoir
divulgué la nouvelle. Responsable de l'initiation des nouveaux, les
"acousmaticiens". |
|
|
|
PHILOLAOS |
Pythagoricien, spécialiste de cosmogonie: la Terre et les autres planètes tournent sur elles-mêmes, et
également autour d'un feu. Ses
considérations sur le rôle du nombre dans l'intelligibilité du monde
constituent un apport original qui va influencer la philosophie de Platon et
d'Aristote. Il
cite les nombres
premiers comme une classe particulière de nombres. |
|
|
|
ANAXAGORE de Clazomène |
Philosophe grec présocratique Traité De la Nature: il y décrit les étapes de la
formation de l’univers, selon un processus cosmogonique d’où rien ne saurait
naître du néant, ni non plus y retourner. Soleil, Lune et étoiles sont des masses de terre. Explique
les phases de la Lune. Travaux sur la quadrature du cercle. |
|
|
– 430 |
ZENON d'Élée |
Invente des paradoxes tels que celui d’Achille et la Tortue
Ces paradoxes
"infinitésimaux" seront
tenus pour plaisanteries jusqu'à leur réhabilitation par les mathématiciens
modernes comme Dedekind ou Weierstrass. |
|
– 430 |
PHIDIAS |
Phi symbolisant le nombre d'or fait
référence à Phidias. |
|
– 470 – 410 (60 ans) |
HIPPOCRATE de Chios |
Mathématicien; premier ouvrage connu
de géométrie, un siècle avant Euclide. Hippocrate de Chios sans doute le premier à utiliser le raisonnement par l'absurde. Travaux sur les lunules et la quadrature du cercle. Ne pas confondre
avec celui du serment sur la médecine. |
|
– 470 – 399 (71 ans) |
SOCRATE |
Connu
pour sa pratique de la dialectique (recherche de la contradiction pour la
dépasser). Homme
qui interroge tout en faisant accoucher les esprits. Condamné
à mort pour corruption de la jeunesse; il a bu la ciguë.
|
|
– 465 – 398 |
THÉODORE de Cyrène |
Mathématicien pythagoricien berbère
spécialiste en géométrie. Spirale de Théodore de
Cyrène |
|
– 370 |
d'Abdère |
Fondateur de
l'atomisme: les différents types d'atomes se déplacent dans le vide et
interagissent, justifiant des phénomènes observés dans la nature. |
|
– 460 – 370 (90 ans) |
HIPPOCRATE de Cos, le Grand |
Serment d'Hippocrate. |
|
– 465 – 398 |
THÉODORE de Cyrène |
Travaux sur les nombres incommensurables découverts
par les pythagoriciens. représentation géométrique. Précepteur de Socrate, Théétète,
Platon. |
|
|
Œnophile de Chios |
Mathématicien
et astronome grec. Compilation
de la science égyptienne. |
|
|
|
HIPPASE de
Métaponte |
Montre que racine
de deux est un nombre irrationnel. A l’époque
beaucoup de mathématiciens n’acceptaient pas l’idée qu’un nombre puisse être
incommensurable. |
|
|
– 465 |
PARMÉNIDE
d'Élée |
Philosophie, logique: rien ne sort
du néant; l'Être est, le non- Être n'est pas. La Terre est sphérique et elle est
située au centre de l'univers. Pose le problème de le trisection de l'angle. |
|
|
– 399 |
HIPPIAS d'Élis |
Interlocuteur de Socrate.
Mathématicien et astronome. Première tentative de trisection de l'angle avec
quadratrice. |
|
|
– 347 |
ARCHYTAS de Tarente |
Gouverneur de Tarente (talon de la botte italienne). Précurseur de la mécanique en mathématiques
(Moyenne). Connait trois des solides réguliers. Courbe d'Architas pour la duplication du cube. |
|
|
– 428 – 348 (80 ans) |
Inventeur
de la logique. Décrit les
cinq
solides réguliers. Sa vision des quatre éléments Double
l'aire du carré
dans son célèbre dialogue sur la
vertu. Voir Trinité |
|
|
– 428 – 347 (81 ans) |
ARCHYTAS de Tarente |
Sans doute
une bonne source des théorèmes énoncés par ses successeurs. De ce fait, il
est l'un des plus grands mathématiciens de l'Antiquité. Actif aussi en
musique, optique et mécanique. Il
résout la duplication du cube d'une manière étonnante, en recourant à l'intersection de trois
solides. |
|
– 369 |
THÉÉTÈTE |
Notions de
nombres carrés, de nombres rectangulaires,
de puissances et de racine carrée. Généralisation
relative aux nombres irrationnels. Il aurait
écrit les tomes X et XIII des Éléments
d'Euclide. Il
découvre les deux derniers des cinq solides platoniciens et
prouve qu'il n'y en a pas d'autres Théétète
est aussi le nom d'un dialogue de Platon. |
|
– 323 |
DIOGÈNE de Sinope dit: le Cynique |
Celui qui
vivait dans le dénuement et dans son tonneau. Voir Syndrome de Diogène
Le dessin est tiré d'un livre de la méthode Assimil. La photo montre la
mise en pratique moderne. |
|
– 355 |
EUDOXE de Cnide |
Le plus grand
savant de cette époque. Euclide à
puisé dans ses traités pour écrire Les Éléments. Méthode d'exhaustion qui a
influencé Archimède. Précurseur du calcul intégral
(infinitésimal). Irrationnels / Volume du cône / séries
géométriques. En astronomie, théorie des sphères homocentriques. Développe la théorie des
"proportions égales" le point de départ de la théorie des nombres réels.
Cette théorie ne fut pas bien comprise du fait du rejet des nombres
irrationnels. Elle fut ignorée durant 2 000 ans, jusqu’à ce que Dedekind et
Cantor créent le système des nombres réels. |
|
|
Dans la
Grèce antique, les soldats échangent des messages codés à l'aide des
scytales. |
|
|
|||
|
IVe siècle av. J.-C. |
École
d'Athènes: Platon, Speusippe – Polyèdres. Rattachés:
Théodore de Cyrène, Théétète – Irrationnelles. Écoles de
Cyzique: Eudoxe de Cnide (Égypte, Tarente) – Arithmétique, sections coniques Péripatéticiens:
Aristote, Autolycos de Pitané, Eudème –
Encyclopédie, histoire |
||
|
– 396 – 314 (82 ans) |
XÉNOCRATE de Chalcédoine |
Propose la
division de la philosophie en logique,
physique et morale ou éthique. Dirige
l'Académie pendant 25 ans. |
|
|
– 384 – 322 (62 ans) |
(Stagire) |
Considéré
dans l'ancien monde comme le plus grand scientifique; le philosophe le plus
influent; et un grand logicien. Formule les règles de la logique sur laquelle repose le
raisonnement déductif, créant la logique classique. À l'origine de l'empirisme qui prétend que les objets
mathématiques préexistent. Les mathématiciens les dévoilent. Mnémotechnique: SPA: Socrate, Platon et Aristote dans l'ordre
chronologique Tuteur d'Alexandre le Grand. |
|
|
– 371 – 287 (84 ans) |
THÉOPHRASTE |
Son surnom veut dire: le Divin
Parleur. Disciple d'Aristote et lui succède à la tête du Lycée. Traités sur la végétation, les pierres, les vents, la
sueur … Modèle pour les caractères de La Bruyère |
|
|
– 380 – 320 (60 ans) |
MENAECHMUS |
Décrit les
sections de coniques :
cercles, ellipses, parabole, hyperboles |
|
|
– 356 – 323 (33 ans) |
ALEXANDRE le Grand |
Roi
de Macédoine (336-323).
Élève d'Aristote. Chef des Grecs contre les Perses. Fonde Alexandrie. S'empare de Babylone
et de Suse, brûle Parsa (Persépolis). Se propage jusqu'à l'Indus. Revient à
Babylone et y meurt. Après sa mort, son empire est partagé entre ses
généraux. Formation des monarchies helléniques. |
|
|
– 296 |
DIODORE CRONOS |
Dialecticien de Mégare (Euclide -). Inventeur de nombreux paradoxes logiques. |
|
|
– 341 – 270 (71 ans) |
Sa morale, la théorie du plaisir (Épicurisme en 306av.
J.-C. ). Opposé: stoïcisme. Comme Démocrite soutient la thèse
des atomes >>> |
||
|
– 310 – 230 (80 ans) |
ARISTARQUE de Samos |
Directeur de
la bibliothèque d'Alexandrie. Précurseur de Copernic: héliocentrisme. Pense que la Terre tourne sur elle-même et autour du
Soleil. Invente une méthode de calcul des
distances relatives Terre - Lune – Soleil. Estime la distance Terre-Soleil à 8 000 km.
Méthodes de mesures avec la Lune |
|
|
|
PHILON de Mégare |
Dialecticien de Mégare (Euclide -). Logique des propositions (si …
alors ..). Disciple de Cronos |
|
|
– 275 |
L'un
des trois géants de l'âge d'or des mathématiques grecques. Élève
d'Aristote. L'un des premiers membres de "l'Université
d'Alexandrie". Publie Les Éléments,
un des textes fondateurs des mathématiques. Démontre qu'il y a une infinité de nombres premiers, l'unicité
de la factorisation des entiers |
||
|
|
Inde |
Les
Indiens développent leurs symboles de nombres brâhmî. |
|
|
|
Sun Zi (SunTzu) |
||
|
|
|||
|
IIIe siècle av. J.-C. |
Archimède
de Syracuse (287-212) – Spirale, grands nombres. Ératosthène
de Cyrène (276-195) – Géodésie, nombres premiers. Apollonius
de Perga (262-180) – Sections coniques |
||
|
|
Alexandrie |
École
d'Alexandrie: vers -290 fondation de la bibliothèque d'Alexandrie, Semblable
à une université d'aujourd'hui. Le phare
d'Alexandrie sera édifié vers -262 par Sostratos de Cnide. Il deviendra l'une
des sept merveilles du monde. |
|
|
– 287 – 212 (75 ans) |
L'un
des trois géants de l'âge d'or des mathématiques grecques. Né à
Syracuse. Fils de l'astronome Phidias qui avait calculé le rapport existant entre
les dimensions du Soleil et de la Lune. Études à
l'école d'Euclide (qui est déjà mort). Ses travaux vont surpasser ceux
d'Euclide. Mathématicien:
calcul de Pi, d'aires, de volumes …. Son
célèbre Eurêka pour la poussée
d'Archimède. Et son non
moins fameux levier. La vis
d'Archimède. |
||
|
– 210 |
NICOMÈDE d'Alexandrie |
Lui aussi
s'attaque à la duplication du cube
ou encore la trisection de l'angle. Il utilise la quadratrice d'Hippias pour résoudre
graphiquement le problème de la quadrature
du cercle. Formule de Nicomède sur les nombres polygonaux. |
|
|
– 279 – 206 (73 ans |
CHRYSIPPE de Soles |
Philosophe
stoïcien. Principal
logicien de l'Antiquité après Aristote. |
|
|
– 276 – 194 (82 ans) |
ÉRATOSTHÈNE de Cyrène (ville de Libye,
aujourd'hui: Shahhat) |
Conservateur
à la bibliothèque d'Alexandrie. Vers -240,
il calcule la longueur du
méridien terrestre avec une précision stupéfiante. Son
célèbre crible
de recherche des nombres premiers. Table des éclipses et catalogue d'étoiles. Mésolabe:
instrument lié aux moyennes
proportionnelles avec le but de résoudre la duplication du cube Voir constellation du Cygne. Voir Les cheveux de Bérénice de Denis
Guedj |
|
|
|
La Septante LXX Bible des
Septante |
À Alexandrie (île de Pharos), soixante-douze lettrés juifs
traduisent la Bible
hébraïque en grec en soixante-douze jours. Discussion d'historiens
autour de 72 ou 70. |
|
|
– 262 – 190 (72 ans) |
APOLLONIOS de Perga |
L'un des trois géants
de l'âge d'or des mathématiques grecques. Géomètre (dit Le Grand Géomètre) et
astronome grec. Il écrit
un ouvrage de référence sur les coniques:
Les Lieux plans, ouvrage qui sera restauré par Fermat. Il analyse les sections d'un cône, et donne un nom à
chaque conique: Ellipse:
omis => en
moins; Parabole,
comparaison => égal, même,
ce qu'il faut; et Hyperbole: en
excès => en plus. |
|
|
– 180 |
DIOCLÈS |
Premier à donner la propriété de la parabole relative au foyer.
Cissoïde de Dioclès destinée à la
résolution de la duplication du cube. Donne la solution de la section
d'une sphère en deux de proportion
donnée. |
|
|
– 247 – 183 (64 ans) |
Hannibal |
Général
et homme d'État carthaginois. En -219,
déclenche la deuxième guerre punique. En
-217, traverse les Pyrénées et les
Alpes avec ses éléphants, bat les Romains sans prendre Rome. En -202,
vaincu par Scipion l'Africain. En -196,
s'exile en Orient et s'empoisonne pour échapper aux Romains. Voir Histoire |
|
|
– 140 |
ZÉNODORE |
Mathématicien
et astronome grec principalement connu par l'intermédiaire de citations. Calcul de
surfaces et de volumes. Affirmations sur des optimum (Isopérimètre): le polygone régulier est celui qui
a la plus grande surface à périmètre donné; etc. |
|
|
– 142 |
CHANG Tshang |
A sans
doute écrit: Neuf chapitres sur l'art des mathématiques. Utilise la
numération décimale; le zéro est figuré par un
espace. Ce livre sera enrichit par Liu Hui
(-220 à -280) et il sera le livre dominant des mathématiques en Asie pour des
siècles. Ce savoir va se diffuser vers l'Inde et au-delà. Les Indiens y
auraient peut être tiré l'idée du zéro. |
|
|
|
Inde |
Système
décimal perfectionné. |
|
|
|
|||
|
– 120 |
HIPPARQUE (Nicée - Rhodes) |
Astronome
et mathématicien grec. Certains disent: le plus grand de tous les temps. Ptolémée
(90-168) est sans doute connu comme le plus grand astronome de l'Antiquité
mais il doit beaucoup à Hipparque. Le père de
la trigonométrie. Astrolabe,
catalogue d'étoiles, précession
des équinoxes, théorie des épicycles. Calcule la
distance Terre-Lune. |
|
|
– 90 |
Théodose de Bithynie |
Mathématicien
et astronome grec qui travailla sur la géométrie de la sphère. Notion de
trigonométrie |
|
|
|
Papier |
en
Chine. Voir Inventions |
|
|
|
Brouette |
en Chine. |
|
|
– 54 |
Titus Lucretius Carus |
De rerum
natura (de la nature des choses), poème qui décrit le monde selon les
principes d'Épicure. Atomiste: Il n’y a rien d’autre dans la nature
que du vide et des atomes, qui sont éternels, absolument pleins et insécables
(atome signifie en grec: qui ne peut être coupé). |
|
|
– 20 |
VITRUVE Marcus Vitruvius |
Architecte romain: technique de construction
de l'Antiquité classique. |
|
|
– 58 – 51 |
Gaule |
Guerre des Gaules Vercingétorix (– 52 Alésia) |
|
|
– 44 |
Jules CÉSAR |
Assassinat de Jules César. |
|
|
– 6 ou – 4 |
Jésus CHRIST |
Naissance à Nazareth Voir pourquoi pas d'année 0. |
|
![]()
|
Suite |
|
|
Voir |
|
|
Sites |
|
|
Cette page |
![]()