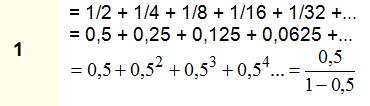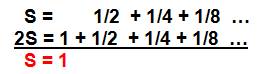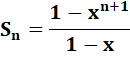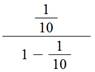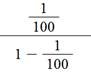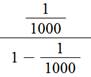|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
![]()
|
SÉRIES en 1 / (1 – x) Notamment pour x < 1. |
Voir DicoMot Maths – Suites et Séries
|
|
||
|
|
|
|
Voir Fractions unitaires / Développement p-adiques
|
|
||
|
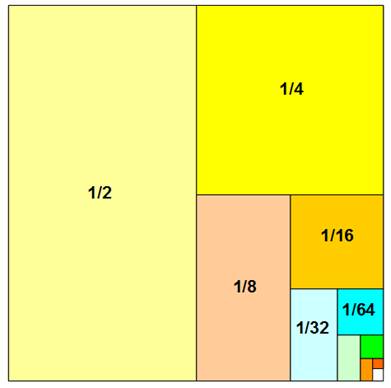
1
= ½ + ¼ + 1/8 + 1/16 + 1/32
+ 1/64 + …
|
|
|
|
|
||
|
|
||
|
On écrit la somme que l'on
soustrait de son double. |
|
|
Voir Identités utiles
En mauve, le cycle des nombres
périodiques
Voir Nombres cycliques
Merci à Frédéric D. pour
ses remarques
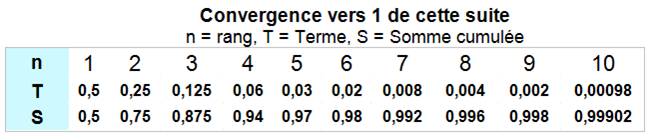
Suite convergence en Formes en xn
/ xn+1
![]()
|
Suite |
|
|
Voir |
|
|
Diconombre |
|
|
Cette page |
![]()