|
Édition du: 02/10/2022 |
Faites
un double-clic pour un retour en haut de
page
![]()
|
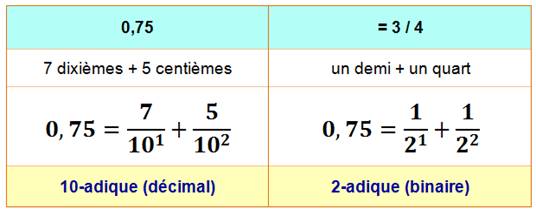
NOMBRES p-adiques Pratique On connaît les fractions
continues pour développer un nombre autrement qu'en indiquant ses
décimales. On peut vouloir utiliser un développement avec
des fractions ayant
toujours le même dénominateur (et ses puissances). Ce sont les
développements p-adiques des
nombres réels. Voyez cet exemple avec 0,75, exprimé sous deux
formes p-adiques:
|
||
|
|
Sommaire de cette page >>>
Approche >>>
Procédure |
Débutants Glossaire |
|
Valeur de la somme de
fractions ayant les puissances de p comme
dénominateur Avec un nombre entier p
comme base du dénominateur, on forme divers nombres décimaux.
Est-il possible d'exprimer
un nombre réel avec les puissances de p comme
dénominateur ?
On remarque en particulier
que:
Conclusion Il semble possible
d'exprimer tout nombre en tant que somme de fractions ayant les puissances
d'un nombre p comme dénominateur. C'est le développement p-adique de ce nombre. |
|
|
Voici comment s'y prendre avec l'exemple
des 2-adiques |
||||||
|
Un nombre réel positif |
n0 |
0,45 |
|
|
||
|
On lui retire sa valeur entière |
e0 |
|
0 |
|
||
|
On conserve la valeur fractionnaire |
f1 |
|
|
0,45 |
||
|
On calcule (avec p = 2) |
n1 =
f1 . p |
0,90 |
|
|
||
|
On lui retire sa valeur entière |
e1 |
|
0 |
|
||
|
On conserve la valeur fractionnaire |
f2 |
|
|
0,90 |
||
|
On calcule |
n2 = f2 . p |
1,80 |
|
|
||
|
On lui retire sa valeur entière |
e2 |
|
1 |
|
||
|
On conserve la valeur fractionnaire |
f3 |
|
|
0,80 |
||
|
Etc. |
|
1,60 |
|
|
||
|
Soit |
|
|||||
|
Programme Maple NP: partie
entière FP: partie
fractionnaire C: matrice une
ligne donnant les numérateurs de 1/pk |
|
|||||
Voir Programmation
![]()
|
Retour |
|
|
Suite |
|
|
Voir |
|
|
Sites |
|
|
Cette page |