|
Édition du: 02/10/2022 |
Faites un double-clic pour un retour en haut de page
![]()
|
NOMBRES p-adiques Opérations Exemples
d'additions, soustractions et multiplications de nombre p-adiques. Les
opérations arithmétiques p-adiques s'effectuent comme les opérations
ordinaires. Les résultats sont tronqués à une quantité de chiffres égale à
celle du plus grand opérande. On
utilise les p-adiques à base 10 (décadiques) pour
se familiariser, mais tout l'intérêt des p-adiques réside dans le fait que p
soit premier. |
||
|
|
Sommaire de cette page >>> En bref >>> Additions >>> Soustractions >>> Nombres négatifs >>> Multiplications >>> Racines carrées |
Débutants Glossaire |
|
Le "p" de p-adique est un nombre premier
et ces nombres s'expriment dans la base
de numération p, donc avec p chiffres de 0 à p – 1. Les nombres décadiques avec la base 10 (chiffres de
0 à 9) n'est pas vraiment p-adique, mais elle est plus simple en tant
qu'introduction aux nombres p-adiques.
|
En base 5 206 = 1×53 + 3×52 + 1×51
+ 1×50
= 225 +
75 + 5
+ 1 On note: 20610 = 13115 Avec des décimales
|
|
|
Un nombre p-adique est un tel nombre écrit en
base p, mais illimité vers la gauche. Le denier chiffre à droite est implicitement
répété à l'infini. Un nombre entier est considéré comme ayant une
infinité de 0 à gauche. |
Exemple de nombre p-adique …1311 = …11111111111311 (ici p est égal ou supérieur à 4) |
|
|
Les calculs (addition, soustraction et
multiplication) s'effectuent comme d'habitude avec les nombres ordinaires. Le dernier chiffre à gauche se répété à l'infini,
à l'exclusion de la propagation de la retenue finale éventuelle. Avec des nombres entiers (répétitions de 0 à
gauche), on retrouve l'addition ordinaire. |
Addition en 5-adique
En rose, répétition des derniers chiffres pour montrer comment est
calculé le dernier chiffre répétitif de la somme (ici: 1 + 2 = 3). |
|
|
L'opposé B d'un nombre p-adique A est tel leur somme est nulle: A + B = 0. D'un manière générale le dernier chiffre de
droite est le complément à p et les autres, le complément à p – 1 . Tout nombre p-adique possède un unique opposé. |
Opposé en 7-adique
En rose, répétition (non nécessaire) pour montrer
la logique du calcul. L'opposé de …321 est …346. |
|
|
Décadique Avec l'addition, on constate que l'opération est normale,
avec ses retenues éventuelles. La somme s'arrête à droite au même niveau que le
plus grand opérande. Certaines additions, du fait de la troncature,
produisent des sommes nulles. Conséquence de cette addition: en décadique,
l'opposé de …9997 est 3. En décadique, les nombres négatifs s'écrivent
sans le signe moins. |
Addition de deux nombres entiers
décadiques
Additions à résultat nul
|
|
|
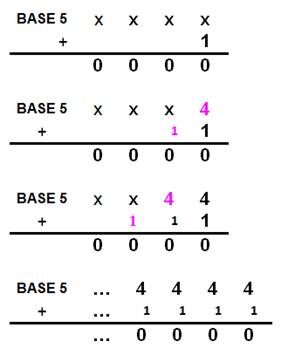
Base p Calculs ordinaires avec troncature comme avec les
décadiques. On note que: À droite, la somme des chiffres vaut 5 soit 0 avec
une retenue. La somme des autres chiffres, qui vaut 4, passe à 0 du fait de
la propagation de la retenue. |
|
|
|
Pour réaliser ou vérifier une soustraction en
base p, il est souvent plus facile de faire la somme des deux nombres du bas
pour retrouver celui du haut. En base 5,
1 – 2 = – 1 = …4444 Avec les nombres ordinaires, on a deux écritures
du même nombre: En base 10,
110 = 0,999…10 Avec les p-adiques cela n'existe pas: En base 5,
– 110 = 0,444…5 |
|
|
|
Le nombre -1 en base 5 comme
exemple de nombre négatif Montrons que:
...4444 est égal = -1 en 5-adique. Posons une soustration
transformée en somme à trou: a0 a1 a2 a3 … ai
… + 1 = 0,000… Les chiffres ai sont
compris entre 0 et 4 en base 5. On a a1 + 1 = 0,
impossible sans retenue. On prend a1 + 1 = 5
(qui en base 5 vaut 10), alors a0 = 4. Le suivant a1 + 1Retenue
= 0, soit à nouveau a1 = 4 avec retenue. Finalement: -1 = …44445 |
|
|
|
Carré de nombres entiers en base 5 Deux présentations: avec indications des 0 à
gauche, ou sans eux. Dans les deux cas, le résultat est tronqué à 11
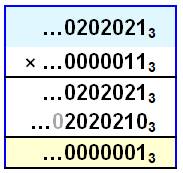
(ou prolonger par des zéros). Produit périodique et entier en
base 3 Dans ce cas les pointillés à gauche signifient
que les chiffres se répètent indéfiniment. Avec 113 qui vaut 410 et le produit obtenu égal à 1, cette
opération indique que: Produit périodique et entier en
base 7 Cette opération montre que: |
|
|
|
Possible en 7-adique. On peut poser une sorte de division comme pour le
calcul
des racines des nombres ordinaires. Ici, avec la multiplication, on vérifie le
résultat:
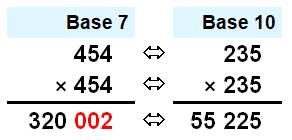
Important Ce calcul montre que la racine de 2 en 7-adique
est un nombre entier. Aucun chiffre à
gauche de 454, sauf des zéros. Il existe de nombreuses racines de 2 en base 7 (Illustration en
bas): Mais, tous les nombres n'ont pas toujours de
racines carrées en base 7: Quelques valeurs: En base 11, racine de 3 = 25, 86, 486, 625, … |
Calcul d'un carré
Détail du calcul via la conversion
en décimal
Autres racines de 2 en base 7
|
|
|
Impossible en 5-adiques |
Car le
carré des chiffres donne les chiffres 0, 1 ou 4 et aucun des autres. |
|
![]()
|
Retour |
|
|
Suite |
|
|
Voir |
|
|
Sites |
|
|
Cette page |