|
Édition du: 24/12/2019 |
|
INDEX |
Carrés dans Carré |
|
![]()
|
N carrés dans un grand carré
Problème d'empilement optimal dans
le plan qui consiste à arranger N carrés identiques dans un carré, le plus
petit possible. |
||
|
|
Sommaire de cette page >>> Cas de 4 et 5 carrés >>> Cas de 10 et 11carrés >>> Récapitulatif pour 1 à
10 carrés >>> Cas de 11 carrés >>> Propriétés >>> Bilan |
Débutants Glossaire |
Anglais: Square packing in a square / Problem
of packing equal squares in a square
|
Cas où N est un nombre carré Dans ce cas,
comme pour N = 4, l'empaquetage est évident. On peut arranger quatre carrés
dans un carré en faisant deux rangées de deux. Avec n = 4, la
taille du grand carré pour des petits carrés de côté unité:
|
|
|
|
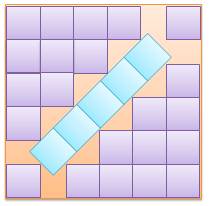
Cas où N = 5 À l'évidence, il n'est pas possible d'obtenir un
remplissage (un pavage) complet. L'arrangement qui minimise la surface du grand carré
consiste à placer le cinquième au milieu des quatre autres avec une
orientation à 45°. L'espacement entre deux carrés est égal à la
moitié de la diagonale (d) du carré central.
La surface perdue (P) est égale à 2,33 sur 7,33
soit 32 %. |
|
|
|
L'illustration
montre les quatre possibilités pour n = 10, avec 1, 2, 3 ou 4 carrés
centraux, orientés à 45°. La construction
ne présente pas de difficulté particulière en s'inspirant de la construction
pour n = 5.
C'est Frits
Gödel qui démontra en 1979 que cet arrangement est optimum pour n = 5. |
|
|
|
Ces
présentations pour n = 10, avec carrés à 45°, peut se généraliser. Avec n = 27 (illustration), le côté du carré est:
On obtient le
même type d'arrangement pour: 5, 10, 27, 38, 52, 67, 84 … Ce sont les
meilleurs connus. Au-delà de 10,
on ne sait pas s'ils sont optimaux. |
|
|
|
À nouveau,
généralisation possible avec cette disposition pour n = 28 que l'on
développer aussi pour 40, 65, 89 … |
|
|
|
Nombreux sont
ceux qui se sont amusé à ce jeux !
Avec une diagonale à deux rangées ou trois rangées. Même des arrangements
improbables comme celui présenté à droite. Chaque fois améliorant
des records, mais trouver la preuve du minimum est une autre histoire. |
|
|
N est la
quantité de petits carrés, C la
longueur du côté du grand carré P est
l'aire de la perte (surface ocre) |
Solutions pour n de 1 à 10
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Le premier
arrangement (à gauche) est réalisé avec cinq carrés orientés à 45°. C =
3,886. Le second (à
droite) correspond au meilleur arrangement connu avec C = 3,8772. Sachant que
Stromquist a démontré que:
C'est le plus
petit cas pour lequel, la solution optimale exige une orientation des carrés
différente de 45°. Ce qui valide la conjecture qu'avait été faite par Marin
Gardner. |
|
|
|
Il n'est pas difficile
de montrer que la longueur du côté C(n) du grand carré en fonction de n est
bornée. Par exemple, 6
carrés tiennent dans un carré de 3 de côté, mais pas dans un carré de 2. |
|
|
|
En 2005,
Nagamochi a prouvé que => Exemples: C(2) = C(3) = C(4) = 2 C(7) = C(8) = C(9) = 3 C(14) = C(15) = C(16)
= 4 |
|
|
|
En 2009, Erich Friedman
prouve les valeurs de C(n) pour: |
2, 3, 5, 7, 8, 14, 15, 24 et 35 |
|
|
Pour une vision synthétique
des connaissances voir la référence anglaise (Friedman).
En annexe (appendix), on y trouve un tableau pour n de 1 à 100 indiquant les meilleurs
arrangements connus, y compris les figures des empilements. Prouver qu'un empilement est
optimum n'est pas simple. La trigonométrie
est mise à contribution. |
![]()
|
Retour |
|
|
Suite |
|
|
Voir |
|
|
|
|
|
Cette
page |