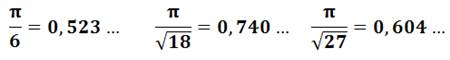NOMBRES – Curiosités, Théorie et Usages Accueil DicoNombre Rubriques Nouveautés Édition du: 14/12/2023 Orientation générale  DicoMot Math Atlas Actualités M'écrire Barre de recherche DicoCulture Index alphabétique Références Brèves de Maths
	Géométrie
Débutants Géométrie	SPHÈRE				Glossaire Géométrie
INDEX Géométrie	Général	Aire et volume	Volumes proches
	Empilements	Calotte …	Et cube	Sphère terrestre
		Sommaire de cette page >>> Approche >>> Kissing numbers >>> Trois types de réseaux >>> Historique >>> Mécanique des sphères >>> Pouliquen et Weidman >>> Secouer ou tourner ? >>> Anglais

EMPILEMENT DES SPHÈRES

Conjecture de Kepler

Les oranges empilée sur l'étal de l'épicier. Vous voyez … C'est simple! Eh bien, non! Trouver quel est l'empilement optimal est un véritable casse-tête pour les mathématiciens. Un problème qui a longtemps résisté aux calculs.

Historique (résumé)

1611 – Johannes Kepler émet sa conjecture: l'empilement de l'épicier est le plus dense possible.

1831 – Gauss démontre que cet empilement est le plus dense des empilements réguliers. Et s'il en existait un irrégulier plus dense?

1998 – Thomas Hales démontre que non, mais personne ne peut la vérifier complètement.

2014 – Il fournit la preuve formelle de la conjecture.

2016 – Maryna Viazovska, a résolu le problème de l'empilement optimal des sphères en dimension 8 et 24 >>>

Suite de l'historique >>>

Voir Lois de Kepler / Preuve des quatre couleurs / Actualités 2016

Anglais: Sphere packing

Ce sujet est hyper-foisonnant et cette page ne constitue qu'un aperçu.

Maryna Viazovska

Maryna Viazovska, née en 1984, mathématicienne ukrainienne à l'Institut Technologique de Lausanne, a résolu le problème de l'empilement optimal des sphères en dimension 8 et 24 en 2016. Elle a reçu le Sastra Ramanujan Award en décembre 2017, prix accordé à un mathématicien de moins de 32 ans ayant réalisé des travaux dans la continuité de Ramanujan. Sa solution implique, en effet, les formes modulaires, un sujet cher à Ramanujan.

Devinette

Quelle est la caisse la plus lourde ? Celle avec une boule de rayon R ou celle avec 5 x 5 x 5 billes de rayon r = R/5 ? Boule et billes sont du même métal.

Solution

La conjecture de Kepler

Cette conjecture énonce que, pour un empilement de sphères égales, en espace libre, la densité maximale est atteinte pour un empilement compact de plans compacts. Cette densité d vaut environ 74,05 %

Elle indique qu'aucun arrangement de sphères de taille égale remplissant l'espace n'a une densité moyenne supérieure à celle des arrangements cubiques compacts (cubiques à faces centrées) et hexagonaux compacts. La densité de ces aménagements est de l'ordre de 74,05%.

Approche
Dans le plan (deux dimensions): avec l'arrangement rectangulaire (orange), une sphère en touche quatre autres; cet arrangement n'est pas optimal. avec l'arrangement hexagonal (rouge), une sphère en touche six autres. C'est mieux! Note: deux types de problèmes proches: l'empilement des disques ou des sphères, et combien de disques ou de sphères peuvent en toucher une autre. Voir Kissing numbers Pour passer en trois dimensions, on ajoute: trois sphères au-dessus et trois sphères en-dessous. Ce qui conduit à: une sphère centrale est entourée de douze sphères identiques; chaque sphère extérieure touche la sphère centrale et quatre autres.	Source image du bas Mathworld
La densité d'empilement (d) est le rapport entre le volume des sphères identiques et celui de la boite les contenant. C'est, en fait, le pourcentage d'espace occupé par les sphères (les boules). La densité maximale (dmax) fut conjecturée par Kepler et démontrée par Hale. Pour éviter les effets de bord, on considère un tas idéal prolongé à l'infini. Par contre, l’équation de l’empilement des sphères est toujours inconnue.	Kepler et ses successeurs connaissent exactement cette valeur de la densité de l'empilement de l'épicier (cubique à face centrées) Le probléme est de montrer qu'il n'en existe pas d'autres plus performant en densité. Régilers ou totament irréguliers.

KISSING NUMBERS – Nombres baisers ou nombres contacts
Combien de sphères identiques au maximum peuvent se ranger autour d'une sphère du même type? On a longtemps hésité entre: 12 (partisan: Newton) et 13 (partisan: Gregory). C'est 12, démontré en 1953 Le tableau donne les "nombres caressants" (kissing numbers) pour les dimensions suivantes: quantité maximale d'hypersphères voisines d'une hypersphère.	Kissing number selon la dimension de l'espace

Voir DicoNombre 12 / 24 / 240 / 196 560

Trois types de réseaux pour un empilement en trois dimensions

Cubique / Cubique à faces centrées / Hexagonal

Densités

Mécanique des Sphères
Densité des disques dans le plan (rectangulaire):
Densité des disques dans le plan (hexagonal:
Constante de l’état désordonné compact:
Constante universelle de la mécanique des sphères:
Densité des oranges déversées sans précaution dans une grande boîte:	0,55
Densité prises par les oranges dans son carton, en secouant: Comparable à l'état désordonné compact, analogue à l’état liquide.	0,6366
État du verre:	> 0,64
Densité maximale d’empilement des sphères: Comparable à l'état du cristal.	0,74

Densité du cube à faces centrées

Voir Densité des disques

HISTORIQUE
Thomas Hariott 1606	L'assistant de Walter Raleigh se pose le problème de l'empilement des boulets de canons. Cet astronome correspond avec Kepler.
Johannes Kepler (1571-1639) 1611	Conjecture que l'empilement optimum est celui des oranges sur l'étalage de l'épicier; soit une disposition cubique à faces centrées. La densité serait alors 0,740… Il existe une infinité d'empilements ayant cette densité. À l'origine, Kepler s'intéressait aux flocons de neige. Il écrit un article qui s'avérera utile en cristallographie: le flocon de neige à six branches. En réalité, il pense que la nature produit les arrangements les plus efficaces comme pour le flocon ou encore les alvéoles des abeilles.
Newton et Gregory 1690	Polémique pour savoir combien de sphères identiques peut-on mettre autour d'une sphère. Problème résolu en 1953.
Lagrange 1773	Prouve que l'arrangement hexagonal des disques est minimal avec une densité de Pi / rac(12) pour un arrangement régulier (réseau)
Carl Friedrich Gauss 1831	Prouve que la conjecture de Kepler est juste pour un arrangement régulier de sphères. Reste à prouver qu'aucun arrangement irrégulier n'est encore plus dense.
Auguste Bravais 1848	Prouve qu'il n'existe que 14 réseaux distincts en trois dimensions
Alex Thue (1863-1922) 1892 et 1910	Il aurait démontré que l'arrangement hexagonal est le plus efficace des arrangements de disques, régulier ou irrégulier. Preuve jugée pas assez rigoureuse pour être retenue.
David Hilbert 1900	En fait, cette conjecture de Kepler devient le 18^e de ses 24 problèmes.
Laszlo Fejes Toth 1940	Prouve que l'arrangement hexagonal des disques est le plus dense de tous, réguliers ou irrégulier.
Rankin 1947	Meilleure solution connue: d = 0,828.
Fejes Toth 1953	Il utilise la décomposition de Voronoï, une construction géométrique classique, et ramène le problème à une question d'optimisation d'une fonction non linéaire à près de 150 variables. Solution impossible à calculer même avec les ordinateurs les plus puissants.
Kurt Schütte et Bartel Leendert van der Waerden 1953	Preuve que seules 12 et pas 13 sphères identiques peuvent se placer autour d'une sphère. (Sphere kissing problem). C'est 24 en 4D. La preuve date de 2003 par Musin qui trouve également les valeurs pour 5D et 24D. Les valeurs pour les empilements d'hypersphères sont connues pour les dimensions 1 à 8 et pour 24
François Le Lionnais 1958	Dans son ouvrage "Les nombres remarquables", il donne 0,779 635 570 0.. = comme étant le meilleur majorant en 1994, valeur trouvée en 1958 par C.A. Rogers
David Scott 1960	Il évalue la densité de l’état désordonné compact avec des billes huilées dans un cylindre.
Buckminster Fuller 1975	Prétend détenir la preuve. Il s'agit du rangement en cube à face centrée sans démontrer que c'est la plus grande des densités.
D.J. Muder 1988 1993	d < 0,77 836… d < 0,77 3055... Ce qui veut dire que l'empilement de l'épicier avec d = 0,740… est proche de ce maximum potentiel.
Wu-Yi Hsiang 1991	Annonce qu'il a la solution. Elle fortement critiquée, notamment par Hales qui est déjà au travail sur ce sujet. Elle ne sera pas validée.
Les Woodcock 1997	Prouve que l’empilement le plus stable est la forme "cubique à face centrée", vision scientifique de l’empilement de l’épicier. Les sphères de la 3^e couche sont bien à la verticale de celles de la première.
Olivier Pouliquen & Patrick Weidman 1997	Ils dépassent le seuil des 0,64 pour s’approcher du 0,74 (En fait 0,70) Ils déplacent les billes dans la boîte par un lent mouvement de cisaillement répété très longtemps. Principe du dispositif de Pouliquen et Weidman: Boîte à fond plat fixe; Côtés pivotants sur charnières fixées au fond; Billes en vrac dedans; Mouvements de va et vient très lents; Les billes prennent progressivement leur empilement le plus dense.

Thomas Hales 1998 Université de Michigan	Prouve la conjecture de Kepler suite à des travaux entrepris en 1992 avec son assistant Samuel Ferguson (Université de Pittsburg, Pennsylvanie). Comme pour les 4 couleurs, il termine la démonstration en épluchant avec un ordinateur les 5094 cas particuliers qui lui restaient. Il utilise une construction voisine de celle de Toth; Méthodes combinatoires plus indirectes avec classification et utilisant la programmation linéaire, les graphes planaires et une utilisation intensive de l'ordinateur. La démonstration implique 300 pages de texte, 40 000 lignes de code (programme) et 3 Goctets de mémoire.
Thomas Hales et son équipe 10 août 2014 Université de Pittsburgh	On dit qu'une équipe de douze mathématiciens aurait donné leur verdict après quatre ans de vérification: la démonstration est probablement juste à 99%. Il n'est pas possible d'assurer qu'aucune faille ne s'y est glissée. En 2003, Hales décide de lancer son projet Flyspeck mettant en œuvre un assistant de preuve par ordinateur. Il avait évalué l'effort à 20 hommes-an. En 2014, annonce officielle de la réussite de ce projet: la conjecture de Kepler est formellement démontrée. La publication officielle date de juin 2017.
Maryna Viazovska et al. Henry Cohn et al. Mars 2016	Si le problème d'empilement des sphères à trois dimensions a été résolu en 1998, celui à 8 et 24 dimensions vient d'être résolu en 2016. Avec 8 dimensions, la structure optimale est décrite par le groupe de symétrie de Lie (E8) et avec 24, c'est le groupe de Leech. Ces groupes sont impliqués dans les codes auto-correcteurs d'erreurs.
L'université d'Utrecht Décembre 2023	Elle montre expérimentalement que le rangement en saucisse (en ligne) est plus efficace que l'empilement pyramidal et cela pour de petites quantités de boules, en fait jusqu'à 56.

Secouer ou tourner ?

Quelle est la façon la plus efficace d'arranger des cubes dans un récipient ? En 2018, une équipe de chercheurs de l'université de Navarre a montré que des rotations énergiques (0,5 g) et alternées (5 000 cycles) du récipient est la plus efficace comparée à de simples secousses.

Application industrielle aux matériaux granulaires ou encore à l'agencement des pilules dans l'industrie pharmaceutique.

English corner

The densest sphere packing a Kepler's conjecture or the Kepler's problem. The stacking of solid spheres in pyramids; the cannonball packing. Not solved until very recently (2014) by Thomas Hales by making extensive use of computer calculations. Density of packing: total area or volume of the objects being packed divided by the total area or volume of the container. In this calculation the method of limits should be applied assuming that the container boundary tends to infinity. The classic sphere-packing problem: find the densest packing of equal spheres in the three dimensional space (d). Kepler's conjecture: d = Pi / Rac(18) = 074...

Voir Anglais

Devinette – Solution

Solution avec calcul

Volume de la boule rouge:

Volume des billes bleues:

Solution avec raisonnement (sans calcul)

Imaginons que chaque petite bille soit dans une petite caisse cubique. Leur empilement reconstitue exactement la grande caisse contenant la boule rouge.

Bilan

Boule et billes ont même volume; même masse et même poids.

Avec des microbilles sphériques de rayon un milliard de fois plus petit, ce serait la même chose !

Retour

Suite	Arrangement optimal des disques Disques dans un rectangle Calotte … Aire et volume	Voir Index Nombres pyramides Nombres octaédriques Points dans le disque
Voir	Cercle Deltaèdre Géométrie – Index Illusions d'optique Nombre d'argent Nombre d'or	Nombres en cercle Polyèdres  Sphère terrestre Triangle sphérique Triangles Vocabulaire de la géométrie
DicoNombre	Nombre 0,740 … Nombre 0,906 … Nombres tétraédriques
Sites	Conjecture de Kepler – Wikipédia Kepler conjecture – Wikipedia Éléments de cristallographie – Voir le réseau cubique à face centrée et ses coupes. Kepler conjecture – Mathworld – Eric Weisstein Sphere packing – Mathworld – Eric Weisstein Kissing number – Mathworld – Eric Weisstein What's the densest sphere packing in a million dimensions? – Henry Cohn, Microsoft Research New England – 2014 (pdf, anglais)
Cette page	http://villemin.gerard.free.fr/Wwwgvmm/Geometri/SpheEmpi.htm