|
|
Définition |
|
|
|
Notations |
|
|
![]()
|
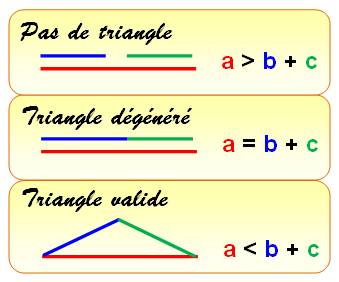
La
distance entre A et B est inférieure ou égale à la somme de la distance entre
A et B et la distance entre B et C. AB Traduit
simplement le fait que pour aller de A à B, le plus court chemin est la
droite et non le détour par C.
Voir Triangles entiers |
|
|
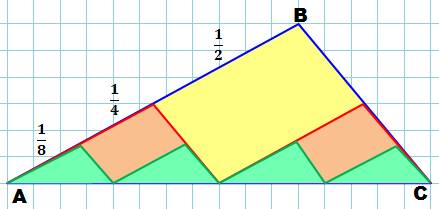
Un
triangle quelconque (périmètre bleu). La
ligne brisée qui passe par les milieux des côtés (rouge). Du
fait du parallélogramme
(jaune), cette ligne rouge a même longueur que la ligne bleue ABC. La
ligne verte est construite de la même manière et sa longueur est égale aussi
à ABC. Et,
cela sans fin. De sorte que la ligne ultime se rapproche du segment AC qui
serait donc de même longueur que la ligne ABC.
Voir Infini |
|
|
Propriétés |
|
![]()
|
Origine |
|
|
Angl |
A two-dimensional
figure with three sides and three angles. |
|
Suite |
|
|
En s |
|
|
Livre |
|
![]()
Voir en Droites et points dans
le triangle
Voir en Types de triangles
|
|
||
|
Ég Isométriques |
|
|
|
Sembl |
|
|
|
Pédal |
|
|
|
Orthique |
|
|
|
Médian |
|
|
|
Pod |
|
|
Voir en Autres types de
triangles
![]()