NOMBRES – Curiosités, Théorie et Usages Accueil DicoNombre Rubriques Nouveautés Édition du: 01/12/2023 Orientation générale  DicoMot Math Atlas Actualités M'écrire Barre de recherche DicoCulture Index alphabétique Références Brèves de Maths
	Carrés magiques
Débutants Carrés magiques	Nature / Structure			Glossaire Carrés magiques
INDEX Carrés magiques Ordres Constructions Magie Jeux de grilles Jeux et énigmes	Débutant	Introduction	Type	Ordre 3
	Nomenclature	Panmagique	Associatif	Antimagiques
	Complémentaire	Gigogne		Antimagiques – R
		Sommaire de cette page >>> Ordre 3 >>> Ordre 4 >>> Ordre 5 >>> Ordre 8

CARRÉS ANTIMAGIQUES

Pas banal ! Contrairement aux carrés magiques, il faut trouver des sommes différentes. C'est un hétérocarré.

Oui, mais avec quelques règles du jeu. Notamment, les valeurs des sommes sont certes différentes, mais consécutives.

Carrés Antimagiques d'ordre 3
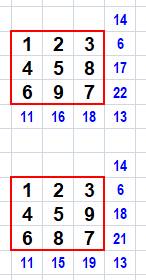
On peut chercher à obtenir des sommes consécutives. Aucun antimagique d'ordre 3 Aucune possibilité avec huit nombres consécutifs pour l'ordre 3. Avec tolérance d'un seul écart de 2, il y a 128 possibilités comme les quatre exemples indiqués.
Exemples de presque anti-magiques. Dans la suite des sommes, une est doublonnée et une autre manquante.

Avec des sommes différentes, il en existe 24 960 d'ordre 3. Dont ces quatre exemplaires à droite. Les deux premiers sont développés ci-dessous:
On peut chercher à minimiser le total des huit sommes. Exemple avec total des sommes égal à 107, le minimum possible. Ils sont 88 avec ce total de 107.
On peut chercher à maximiser le total des huit sommes. Exemple avec le total maximum de 133.

Carrés Antimagiques d'ordre 4 ou carrés magiques hétérogènes (heterosquares)
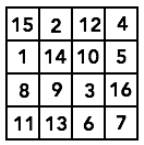
Le plus petit carré magique est d'ordre 4. Ils sont 299 710. Voici deux exemples: Nombres de 1 à 16 Sommes de 29 à 38
Sommes de 30 à 39

Carrés Antimagiques d'ordre 5
Exemple: Nombres de 1 à 25 Sommes de 59 à 70

Carrés Antimagiques d'ordre 8
Exemple: Nombres de 1 à 68 Sommes de 252 à 269

ENGLISH CORNER
Anti-Magic Squares An Anti-Magic Square (AMS) is an arrangement of the numbers 1 to n² in a square matrix such that the row, column, and diagonal sums form a sequence of consecutive integers. An array of consecutive numbers, from 1 to n², where the rows, columns and two main diagonals sum to a set of 2(n + 1) consecutive integers.

Suite	Carrés antimagiques - Variante	Carrés magiques – Index
Voir	Carrés – les nombres Carrés en géométrie Carrés mystérieux Géométrie – Index Humour – Index	Jeux – Index Nombres consécutifs Nombres magiques - Index Rubriques débutants – Index Sudoku
Sites	The anti-magic square project – John Cormie Anti-magic square – Arie Breedijk
Cette page	http://villemin.gerard.free.fr/Wwwgvmm/CarreMag/CMAnti.htm