|
|||||||||||||||||||||||||||
![]()
|
Carrés magiques GIGOGNES ou CONCENTRIQUES Carrés magiques à
l'intérieur d'un carré magique, comme l'emboitement des poupées russes. Occasion de découvrir une nouvelle
méthode pour construire des carrés magiques d'ordre pair. |
Anglais: Bordered or
concentric magic squares
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
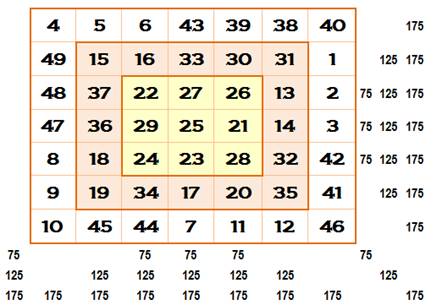
Exemple Grand
carré: carré magique (diabolique) d'ordre 5:
Carré
au centre: carré magique (jaune) d'ordre 3:
|
Carrés magiques 5x5 gigognes parfaits. |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
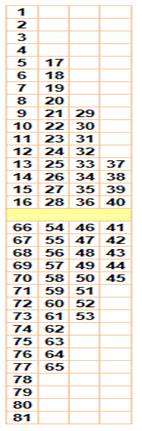
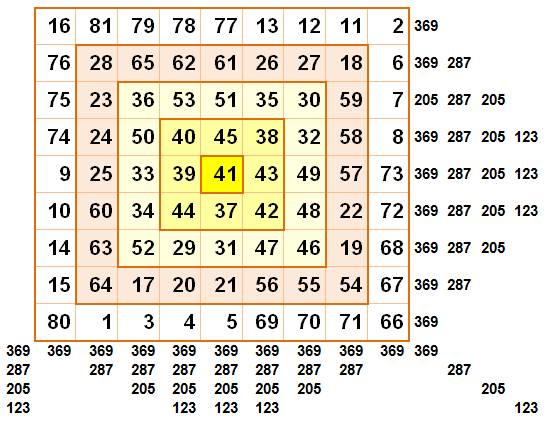
Exemple de carré magique 9x9 quadri-gigogne parfait Carré réalisé par Frénicle de Bessy (1602-1675) À gauche, les nombres utilisés dans chacune
des couronnes. |
|
|
|
|
Voir Carrés
magiques 5x5 / Carrés 6x6 / Carrés 8x8 / Carré 10x10
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Voir Carré magique gigogne 25x25
|
|
|
|
|
|
|
|
||
|
D'un carré d'ordre
4 nous allons passer à un carré d'ordre n = 6. Sa somme magique est égale à : ½ n (n² + 1) = 3 x 37
= 111. |
||
|
(Il
faut soustraire 2n – 2).
|
|
|
|
|
|
|
Voir Autres méthodes
de construction
|
|
|
|
|
|
![]()
|
Suite |
|
|
Voir |
|
|
Sites |
|
|
Cette page |
![]()