|
Édition du: 22/11/2023 |
|
INDEX lettre I |
Dictionnaire de base du vocabulaire des mathématiques |
|
|
Faites
un double-clic pour un retour en haut de
page
Pour
trouver un mot: Ctrl F et tapez le mot
cherché
|
Avertissement Dictionnaire pour débutants,
juniors, novices, "nuls" … !!! On privilégie la compréhension par rapport à une rigueur mathématique !!! Les liens permettent de compléter et d'approfondir Pour une
version plus académique se reporter aux ouvrages spécialisés. |
Légende Parfois,
plusieurs définitions sont données: de la plus "intuitive" à la
plus correcte mathématiquement Mode de recherche: si vous ne trouvez
pas symétrie centrale à symétrie, voyez à centrale, par exemple. Difficulté: * notion avancée;
** notion complexe. |
![]()

i minuscule: nombre complexe
tel que: i² = -1.
Avec cette convention, un nombre complexe s'écrit a + ib.
Racine
du polynôme
x² + 1 = 0.
– v. Nombres
complexes
– a. Complex numbers

Icosaèdre: polyèdre
à vingt faces.
Les faces de l'icosaèdre régulier sont des triangles
équilatéraux.
– v. Icosaèdre,
Les
59 icosaèdres
– a. Icosahedron
Icosagone: polygone
à 20 côtés.
Chacun des angles d'un octogone
régulier vaut 162°.
– v. Icosagone
– a. Icosagon
IDE (Integrated
Development Environment: environnement de programmation intégré).
Comporte
un éditeur de code (html, script ..),
des outils automatiques de fabrication du code, un compilateur faisant
passer du code source au code exécutable, et un déboguer (outil de mise au
points du logiciel).
– v. POO, langage Python
(IDLE)
Idéal** sous-ensemble
tel que toutes les opérations dans l'ensemble donne un résultat appartenant à
ce sous-ensemble (stabilité).
– ex. ![]() ; I est un idéal de
A.
; I est un idéal de
A.
Les idéaux de l'anneau ![]() sont les sous-groupes
sont les sous-groupes ![]() avec
avec ![]() .
.
– v. Nombres idéaux, structures algébriques
– a. an ideal of a ring is a special subset of its elements.
Les idéaux isolent des sous-ensembles parmi
les nombres entiers, comme les nombres pairs ou les multiples de 3.
Par exemple: l'addition et la soustraction
de nombres pairs préservent la régularité, et la multiplication d'un nombre
pair par un nombre entier donne un nombre pair. Ces propriétés (dites de
fermeture et d'absorption) sont les propriétés qui définissent un idéal.
Un idéal peut être utilisé pour construire
un anneau quotient de la même manière que, en théorie des groupes, un
sous-groupe normal peut être utilisé pour construire un groupe quotient.
Idempotence**: opération qui a le
même effet qu'on l'applique une ou plusieurs fois.
La
valeur absolue est idempotente.
Un élément a de R est idempotent si a2
= a.
Si a est idempotent alors 1 – a l'est aussi.
Dans ![]() les éléments idempotents sont {1, 4 et 9}.
les éléments idempotents sont {1, 4 et 9}.
– v. Nilpotent, vocabulaire
des structures algébriques
– a.
Idempotence
Un élément x d’un ensemble E muni d’une loi
de composition interne (notée *) est idempotent si, composant x avec lui-même,
on trouve x comme résultat : x * x = x.
Dans l’ensemble des entiers naturels, muni
de la multiplication, les seuls éléments idempotents sont 0 et 1 : 0 x 0 =
0 et 1 x 1 = 1.
Dans l’ensemble P(E) des parties d’un
ensemble E, muni de la loi intersection, tout élément est idempotent, car, pour
toute partie A de E, l’intersection de A avec elle-même est égale à A : A ∩ A = A.
De même pour P(E) muni de la loi réunion,
tout élément est idempotent, car, pour tout A de P(E), on a : A U A = A.
Si tout élément de E est idempotent, la loi
* est dite idempotente et E lui-même est dit idempotent.
Identité
(algébrique): relation toujours valable quelles que soient
les valeurs des variables.
– ex. a² – b² = (a – b) (a + b); sin²(a)
+ cos²(a) = 1.
Ceci à la différence d'une équation
qui n'est satisfaite que pour certaines valeurs de la ou des variables.
Une équation de degré n qui possède plus de n racines est une identité.
– a.
Identity
Identité ou relation identique: dans un ensemble
E, relation qui ne comprend que tous les couples identiques sur E.
– not. La
relation identique sur un ensemble E est notée : IE.
–
ex. E = {1, 2, 3}, alors IE ) {(1,1), (2,2) (3,3)}
Identité (application – ou fonction -): application
de E dans E qui associe l'élément lui-même à tout élément.
Application qui n'a aucun effet lorsqu'appliquée à un élément.
– a. Identity function
Identité (transformation - ): transformation
qui ne change rien comme une rotation
d'angle zéro, par exemple.
Identité de Bézout ou théorème de Bachet-Bézout
Les
nombres a et b sont étrangers si et seulement si il existe u et v tels que au
+ bv = 1.
– v. Identité de Bézout
– a. Bezout's identity
Identité remarquable: formule
de base, à retenir, comme (a + b)² = a²
+ 2ab + b² .
Elles servent à effectuer une transformation: factorisation ou développement.
– v. Identités remarquables, binôme
de Newton, factorisation
– a. Remarkable identities
![]() Square of an addition: (a + b)2 = a2 + b2
+ 2ab
Square of an addition: (a + b)2 = a2 + b2
+ 2ab
![]() Square of a subtraction:
(a - b)2 = a2
+ b2 – 2ab
Square of a subtraction:
(a - b)2 = a2
+ b2 – 2ab
![]() Addition
multiplied by subtraction: (a + b)·(a – b) = a2 - b2
Addition
multiplied by subtraction: (a + b)·(a – b) = a2 - b2
Identités (ou formules)
trigonométriques: formules de transformation diverses à connaitre en trigonométrie: sinus
ou cosinus de sommes, passage à l'angle moitié ou double, etc.
– v. Relations
trigonométriques
– a. Trigonometric identities
 if … then … else … anglais pour si …
alors … sinon … Instruction conditionnelle en informatique.
if … then … else … anglais pour si …
alors … sinon … Instruction conditionnelle en informatique.
Si une condition logique est satisfaite alors un traitement est réalisé; sinon,
c'est un autre traitement.
– v. Conditions
Iff (if and only if): anglais pour si et seulement si
(abrégé en: ssi).
– v. Ssi, équivalence,
 Illusion d'optique: figure, image qui défie la logique de notre
entendement.
Illusion d'optique: figure, image qui défie la logique de notre
entendement.
– ex. Le trident impossible (illustration)
– v. Illusions
d'optique
– a. Optical illusions
Image: dans une transformation,
un point M (dit antécédent) est transformé en un point
M' dit son image.
– v. vocabulaire
des structures algébriques
– a. Image
Image de x par une fonction: valeur de
l'ordonnée y pour le point de la courbe représentative de la fonction ayant x
pour abscisse.
Avec x donné, la valeur de y est l'image; avec y donné,
la valeur de x est l'antécédent.
– a. the image of a function is the set of all output values it may produce.
Image de x par une application: pour une application: f : E → F
Pour tout élément x de E,
l’unique élément f(x) qui lui est
relié dans F est appelé image de x par f, et dans ce cas on dit que x est un antécédent de f(x)
par f.
L’ensemble des images des éléments de E est appelé ensemble image de f,
ou simplement image de f. L'ensemble des antécédents est l'image réciproque
ou préimage.
– a.
Image, inverse image or preimage
Imaginaire (nombre -): nombre associé à i,
racine de -1.
Nombre imaginaire ou nombre imaginaire pur: nombre complexe dont la partie
réelle est nulle. Son carré est un nombre réel négatif (ou nul). La racine
carrée d'un nombre réel négatif est un nombre imaginaire pur.
Notation: z = i · b
– v. Nombre imaginaire
– a. Imaginary number: a real number multiplied by the imaginary unit i.
Immersion**: une application
différentiable d'une variété différentielle dans une autre, dont la
différentielle en tout point est injective.
– a. Immersion
– note: Plongement: Embedding ou Imbedding
Impair
(nombre -): nombre de la forme 2k + 1.
Il reste 1 dans la division par 2.
– propriété: la somme des nombres impairs successifs est un carré:
1 + 3 + 5 + 7 + … + (2n-1) = n²
– v. Pair et
impair, gnomon
– a. Odd (qui veut aussi dire: étrange, curieux, singulier)
– humour anglais: 3 is an odd prime, but 2 is even more odd because it is even
Impaire (fonction -): telle que f(-x) = -
f(x). Alors: f(x) + (f-x) = 0
– ex. x3, sin (x).
– a. Odd function
Implication: un opérateur
binaire en calcul des propositions.
La
proposition P ![]() Q (lire
P implique Q) est toujours vraie, sauf si P est vraie et Q est fausse.
Q (lire
P implique Q) est toujours vraie, sauf si P est vraie et Q est fausse.
– v. Implication
– a. Material conditional or material implication: a formula P ⇨
Q P → Q is true unless P is true and
Q Q is false.
Implication réciproque: une proposition
interchangeant la prémisse et la conclusion d'une implication.
Implication: A alors B; sa réciproque B
alors A. P ![]() Q sa réciproque Q
Q sa réciproque Q ![]() P.
P.
– a. Converse logic, implication converse
Implication (démonstration par -): basée sur le principe que A impliquant B et B
impliquant C, alors A implique C.
– v. Déduction
 Implicite (fonction – ou équation -): de la forme R(x, y,
z, …).
Implicite (fonction – ou équation -): de la forme R(x, y,
z, …).
– ex. équation implicite du cercle
unitaire: x² + y² – 1 = 0
En général, il est difficile de calculer l'expression d'une variable (y) en
fonction d'une autre (x).
En programmation, le mode implicitplot permet la représentation de telles
fonctions: Exemple de programme et de son
rendu:
![]()
Impossible (nombre -): tout premier nom
qui désignait les nombres
complexes.
Improbable (événement): cet événement ne
peut pas se produire.
Événement dont la probabilité
d'occurrence égale à 0.
Contraire de certain.
Ne pas confondre avec affirmation fausse.
– a. The event is certain, impossible or probable
Impropre (fraction -): fraction
dont le numérateur est plus grand que le dénominateur.
Elle est propre dans le cas contraire.
– a. Improper fraction
Incertitude: marge d'erreur sur
une mesure, connue ou inconnue.
L'incertitude, qu'elle soit absolue ou relative, s'écrit toujours avec un seul
chiffre significatif.
– syn. imprécision
– Note.
ne pas confondre avec erreur de mesure
– v. Incertitude
et précision
Incertitude absolue: incertitude maximale. Elle est indiquée avec la même
unité que la mesure. Elle est notée: ![]()
Incertitude relative: rapport entre incertitude absolue et la mesure,
exprimé en pourcentage. ![]()
Incertitude (de mesure): en métrologie, l'incertitude caractérise la
dispersion des mesures. Valeurs objet de calculs statistiques (moyenne,
écart-type …)
– v. Statistiques
– a. Measurement uncertainty
Attention !
|
Tous ces termes de métrologie (incertitude, erreur,
précision, justesse, fidélité …) sont définis précisément par des normes
internationales. Pour un usage professionnel se reporte à ces textes. |
Incident (arc, sommet
…): signifie relié à, en relation avec.
Un point est incident à une droite s'il est sur la droite, autrement dit
si la droite passe par ce point.
Un arc est incident à un sommet ou une arête est incidente à un sommet si ce
sommet est l’une des extrémités de cet arc ou de cette arête.
Un sommet d’un graphe est incident à une arête ou un arc s’il est situé à l’une
des deux extrémités de cette arête ou de cet arc.
– a. Incident: the binary relations describing how
subsets meet
Angle d'incidence: angle entre le
rayon et la perpendiculaire du lieu considéré.
En optique, angle entre la direction de propagation de l'onde incidente et la
normale au dioptre ou à l'interface considérée.
– a. Angle of incidence: angle between a ray incident on a surface and the line
perpendicular to the surface at the point of incidence
Inclusion, inclus: l'ensemble A est
inclus dans l'ensemble B (A Ì B) si tous les
éléments de A appartiennent aussi à B.
A est un sous-ensemble de B ou une partie de B; B est un sur-ensemble
de A.
Relation d'ordre entre ensembles
– v. Union, intersection, appartenance
– a. Subset: all elements of A are also elements of B. B is then a superset of
A.
Incompatibles:
deux
événements qui ne peuvent pas se réaliser en même temps, simultanément;
événements disjoints.
– v. Indépendant, vocabulaire
du dénombrement et des probabilités
– a. Pairwise disjoint
Incomplétude (théorème
d'-)** avec un minimum d'axiomes,
il est possible construire une théorie mathématique.
Cependant, le théorème d'incomplétude dit qu'il est impossible que cette
théorie soit complète. Il y aura toujours des vérités qui ne pourront pas être démontrées.
L'incomplétude, c'est l'incapacité de concevoir un système mathématique qui
englobe toutes les vérités mathématiques. Il y aura toujours des
"trous".
Découverte et démontrée par Kurt Gödel (1931).
– v. Indécidable, incomplétude
– a. Gödel's incompleteness theorems. They are concerned with the limits of provability in
formal axiomatic theories.
Inconnue: variable d'une équation que l'on cherche à calculer.
Notées: x, y ou z.
Nommées: solutions ou racines
dès que les valeurs sont connues.
– v. Variable
– a. Unknown. The values of the unknowns that satisfy the equality are called
solutions of the equation
Incrément: incrémenter c'est additionner en informatique, c'est ajouter une quantité entière à un compteur.
Ex: incrémenter par 1. Un incrément est une quantité à ajouter.
Logiciel Maple: a : =
a + 1 a pour effet d'ajouter 1 au
paramètre a.
Logiciel Python:
a += 1 a pour effet d'ajouter 1 au paramètre a.
– a. Increment and decrement operators
Incrémenter, sans autre indication, est souvent synonyme d'ajouter une
unité. Incrémenter un compteur = le
faire passer à la valeur suivante.
Décrémenter, c'est soustraire.
Indécidable
(proposition - )** quelle que soit la méthode utilisée, il est
impossible de dire si la proposition
est vraie ou fausse.
La réponse échappe à la théorie.
– v. Indécidable,
incomplétude, oméga de Chaitin,
machine
de Turing
– a. Undecidable, decidability of a logical system or of a theory
Indépendant: en probabilité, si
deux éléments sont totalement autonomes.
L'un n'influence en rien l'autre.
Alors ![]()
– v. Incompatibles, probabilités
– a. Indepensdence: the occurrence of one does not affect the probability of
occurrence of the other.
Indépendants (vecteurs): ni colinéaires,
ni coplanaires.
– v. Colinéaire et coplanaire
– a. not collinear and not coplanar vectors
Index: Entier naturel
repérant la position d'un élément dans un ensemble, une base de données.
Par extension, données préétablies qui donnent le moyen de pointer (de
retrouver rapidement) des informations dans un livre, une encyclopédie ou une
base de données.
– v. Indice, pointeur
– a. Index, data base index
Index: en imagerie, cartographie,
marqueur (comme un réticule) repérant la position d'un élément pour la
communiquer.
Aussi: nomenclature des cartes renvoyant aux cartes détaillées par un numéro,
dit index.
Indicatrice
Fonction indicatrice ou
caractéristique* de l'ensemble F relativement à E: elle indique si un élément x de E
appartient à F (valeur 1) ou non (valeur 0).
– a. Indicator function
Fonction indicatrice (analyse convexe): fonction qui vaut 0 sur F et
l'infini sur le complémentaire de F dans E.
Characteristic function in convex analysis
Indicatrice d'Euler ou totient : notée Phi (n),
c'est la quantité de nombres premiers avec n,
inférieurs à n.
![]()
– a. Euler's totient function counts the
positive integers up to a given integer n that are relatively prime to n.
 Indicatrice de Tissot: en cartographie, ellipse
qui représente les déformations de la carte selon la projection utilisée. Avec
la projection de Mercator
l'indicatrice de Tissot (illustration) est
un cercle de petite taille à l'équateur et
plus grand pour les grandes latitudes.
Indicatrice de Tissot: en cartographie, ellipse
qui représente les déformations de la carte selon la projection utilisée. Avec
la projection de Mercator
l'indicatrice de Tissot (illustration) est
un cercle de petite taille à l'équateur et
plus grand pour les grandes latitudes.
–
a. Tissot's indicatrix, Tissot's ellipse
Indice: A1 se lit "A
indice 1". A2 se lit "A puissance 2", et le
nombre 2 est l'exposant (on peut dire aussi: A exposant 2).
L'indice indique le numéro d'ordre d'un élément dans une suite d'éléments.
Utilisés pour repérer les
termes d’une suite (ou, plus généralement, les éléments d’un ensemble
dénombrable), on les note u1
et on lit : u un, ou : u indice un, u2 … Les nombres 1, 2, . ., sont les indices.
– v. Exposants
et indices
– a. Index
Indice muet: indice utilisé dans
une formule ou un nombre doit prendre différente valeurs successives entre deux
bornes.

Indice base 100: comparaison de
l'évolution de valeurs en supposant que l'un d'entre eux vaut 100.
– ex. Le prix d'un paquet de café selon les années en donnant une valeur 100 en
2005, par exemple.
– v. Règle
de trois, quatrième
proportionnelle, pourcentage
– a. The base value always has an index
number of 100.
Individu: en statistique, un individu de la population
étudiée.
Ce peut être un objet.
– v. Statistiques
– a. Sample: one (or several) of the
population. Ex. one of the math classes
Indo-arabe
(numération -): notre système de numération décimale.
– v. Numération
décimale, origine
des nombres
– a. Hindu–Arabic numeral system.
Induction: généralisation à
partir de cas singuliers.
Raisonnement
par induction ou par récurrence.
Preuve par induction ou preuve par récurrence.
– en bref: Si vrai dans un cas particulier et si vrai lors d'un passage au
suivant, alors vrai dans tous les cas.
– v. Principe
de ce type de raisonnement, de démonstration
– a. Mathematical induction, a mathematical proof technique.
Induction et déduction: Voir Déduction
Inégalité: comparaison entre
deux nombres:
a
< b a est (strictement) inférieur à b;
a ≤ b a est inférieur ou égal à b;
a > b a est (strictement) supérieur à b;
a ≥ b a est supérieur ou égal à b.
On peut ajouter ou retrancher le même nombre de chaque côté sans changer le
sens de l'inégalité.
On peut multiplier chaque côté par le même nombre positif sans changer
le sens de l'inégalité. En multipliant par une nombre négatif, on change
le sens de l'inégalité.
– v. Inéquations,
relation d'ordre
Inégalité
triangulaire: Elle traduit simplement le fait que pour aller
de A à B, le plus court chemin est le segment AB et non le détour par C.
Dans un triangle, la somme des longueurs de deux côtés est toujours plus grande
que celle du troisième côté.
– v. Inégalité
triangulaire
– v. Triangle inequality
Inégalité linéaire: inégalité qui
implique une fonction linéaire.
– ex: 3x – 2y > 5
– a. Linear inequality
Inégalité matricielle linéaire: inégalité linéaire
dont les coefficients sont des matrices.
Linear matricial inequality (LMI).
Inéquation: équation dans
laquelle le signe égal est remplacé par un signe d'inégalité.
– ex.
x – 2 < 3x – 4 est une inéquation du premier
degré.
– v. Inéquation,
différent, supérieur, inférieur, égal, inégalité
– a. Inequation
Inertie (centre d'-) ou
centre de masse: le centre d’inertie d’un ensemble de points pondérés est le barycentre de ces points affecté de coefficients
correspondant à leurs masses respectives.
Ce centre d’inertie se confond avec le centre
de gravité.
– v. Centre de gravité, centre d'inertie
– a. Center of mass, balance point: the unique point where the weighted
relative position of the distributed mass sums to zero.
Inférence:
Tirer
une conclusion d'un fait, d'une proposition tenue pour vraie.
Opération intellectuelle qui fait passer d'une affirmation à une
conclusion.
– étym. Latin: in et fero porter dans
– ex. déduction ou induction
– a. Inférence: a conclusion reached on the basis of evidence and reasoning
Inférieur: synonyme de plus
petit, noté a < b
– v. Égal, différent, supérieur, inégalité, comparaison
– a. Inferior, less; The notation a < b means that a is less than b.
The notation a ≤ b or a ⩽ b means that a is less than or equal to b
Borne supérieure / inférieure, limite supérieure / inférieure
La borne supérieure (ou le supremum) d'une partie d'un ensemble
(partiellement) ordonné est le plus petit de ses majorants.
La borne inférieure (ou l'infimum) d'une partie est le plus grand de ses
minorants.
– a. Infinimum and supremum, lower
bound, lower limit
Les expressions anglaises upper bound et lower
bound ne correspondent pas à borne
supérieure et borne inférieure, mais
à majorant et minorant,
respectivement ;
Borne supérieure
se traduit par least upper bound ou supremum
et borne inférieure par greatest lower bound ou infimum.
Informatique: traitement
automatique de l'information à l'aide d'ordinateurs et de programmes.
– v. Informatique, programmation
(logiciel), historique
– a. Computer science, data processing, software
Infini: nombre encore plus
grand que le plus grand imaginable.
Synonyme de sans fin, illimité, et noté ![]() .
.
– v. Infini, Aleph,
diagonale
de Cantor, hypothèse du
continu.
– a. infinite; courbe infinie: endless curve
Infini potentiel (ou en puissance): sans borne, sans
limite, plus grand que toute quantité finie donnée.
Infini actuel (ou en acte): infini considéré comme un tout. Il est en
bijection avec l'une des ses partie autre que l'ensemble vide ou lui-même.
Ex: Les entiers forment un ensemble actuel. Les nombres pairs peuvent y être
mis en bijection avec les nombres entiers.
Remarque:
Ces
deux notions sont subtiles et d'intérêt historique ou épistémologique.
Inflexion (point d'-): point d'une courbe
plane avec changement de concavité
Point
d'une courbe où celle-ci se trouve de part et d'autres de la tangente en ce
point.
En s'approchant de ce point la pente de la tangente progresse (ou régresse) et
au-delà la pente change de sens; comme le milieu de la forme en S d'un
toboggan.
– a. Inflection
point: point on a curve at which the curvature changes sign.
Ingénieur
(notation -): écriture d'un nombre en puissances de 1000.
– ex. 123 456 789 s'écrit; +123,456 789 106
![]() un signe plus ou moins;
un signe plus ou moins;
![]() un nombre à trois chiffres, la mantisse;
un nombre à trois chiffres, la mantisse;
![]() les nombres après la virgule sont groupés en blocs de trois; et
les nombres après la virgule sont groupés en blocs de trois; et
![]() une puissance de dix en 3k, le nombe 3k est l'exposant.
une puissance de dix en 3k, le nombe 3k est l'exposant.
– v. Notation ingénieur
– a. Engineering notation
Injection ou
application injective* tous les points M de E ont une
image P en F, mais il se peut que certains
points P de F n'aient pas d'antécédents dans E.
Application f d'un ensemble
E vers un ensemble F dans laquelle des éléments
distincts de E ont des images
distinctes en F.
– relation: bijection =
injection + surjection
– v. Bijection, vocabulaire
des structures algébriques
– a. one to one
Innumérisme: grande difficulté
avec les chiffres et le calcul comme l'illettrisme avec les mots.
– v. Innumérisme
– a. innumeracy.
Inscriptible: un polygone est inscriptible
dans un cercle si tous ses sommets sont situés sur le cercle.
Inscrit (angle -): un angle
inscrit est interne à un cercle
avec son sommet sur le cercle.
– v. Triangles et
cercles
Inscrit (polygone -): un polygone
inscrit a tous ses sommets sur un même cercle.
Ex: un quadrilatère inscriptible.
– v. Quadrilatère inscriptible
et théorème de Ptolémée.
– a. Cyclic quadrilateral, inscribed quadrilateral; whose vertices all lie on a
single circle.
Inscrit (polyèdre -): Un polyèdre
inscrit a tous ses sommets sur une même sphère.
Inscrit (cercle -): un cercle
inscrit dans un polygone est tangent à
chaque côté du polygone.
– v. Cercle inscrit
– a. Incircle
Instancier: en informatique,
c'est donner une valeur à un paramètre.
C'est affecter une valeur à un paramètre.
C'est remplir une case-mémoire. – ex. A = 10.
Souvent un symbole spécial distingue la simple égalité de l'instanciation. –
ex. A := 10. En maths, on dirait substituer. On pourrait aussi parler d'application
numérique.
–
étym. de l'anglais: instance, exemple (for instance)
– a. Instantiate
Instruction: opération
élémentaire dans un programme informatique.
– ex. Additionner cette information avec celle de l'adresse mémoire 2421,
mémoriser l'information obtenue à l'adresse mémoire 242 …
– v. Programmation
débutant, programmes,
algorithme
– v. Instruction (computer science): single operation of a processor.
INT: fonction
"integer" en programmation.
Elle donne les chiffres avant la virgule.
– ex. INT(3,2) = 3, INT(-3,2) = -3.
– v. Arrondis
et ses cousins
Integer: anglais pour nombre
entier.
Abrégé en int en informatique.
Ex: Pour être sûr que la variable âge sera comprise comme un nombre on notera int(âge) en Python.
Avec Maple, pour tester si
variable est un nombre entier on écrira: type(âge,
integer).
Intégrale* aire de la surface
limitée par une courbe.
Intégrale d'une fonction f sur l'intervalle [a, b] égale aire de la surface
limitée par la courbe représentant la fonction, l'axe des x et les deux
verticales d'abscisse a et b.
– notation: ![]() .
.
– note: Le mot intégral suggère quelque chose d'entier, de complet. Ex:
Il m'a payé intégralement.
– v. Dérivée,
dérivées
usuelles, intégrale,
primitives
usuelles
– a. an integral assigns numbers to
functions in a way that describes displacement, area, volume, etc.
Calcul intégral** ou intégration: dessinez une
courbe dans un repère, l'intégrale représente l'aire de la zone entre la courbe
et l'axe des abscisses.
Calcul de grandeurs comme une aire
par la simple connaissance de la courbe qui l'engendre.
Connaissant les petites variations locales de la fonction en déduire la
fonction.
Calcul par lequel on remonte des infiniment petits aux quantités finies dont
ils dérivent.
– v. Calcul intégral
– v. Integration
Intégre (anneau -)**: Un anneau
commutatif unitaire différent de l'anneau nul et qui ne possède aucun diviseur
de zéro.
Le produit de deux éléments non nuls peut y être nul, on dit que l'anneau n'est
pas intègre.
– a. En nombres décadiques (les chiffres à gauche sont
ignorés): …625 × …376 = …000 (en nombres ordinaires: 250 000).
– a. Domain, integral domain: is a nonzero commutative ring in which the
product of any two nonzero elements is nonzero
Intégrité du signal: en traitement ou de
transmission de messages, qualité assurant que le message n'est pas altéré ni
par la technique ni par la malveillance humaine.
– v. Chiffrement,
chiffre
– a. Signal intégrity (SI)
Intelligence
artificielle: mise en œuvre de l'informatique logique
pour entrer en mimétisme avec l'intelligence humaine.
– v. Intelligence artificielle
– a. Artificial intelligence (IA)
Intensité: valeur numérique
d'une grandeur
comme la force
ou un courant …
L'intensité du courant électrique se mesure en ampères (A).
– v. Loi
d'Ohm, module
– a. Intensity, electric current
Intercepter:
voisin
de englober, embrasser.
– ex. un angle
qui intercepte un arc de cercle
– v. Sous-tendre, capable
(arc), angles et
cercles
– a. Intercept
Intérêt: montant à payer
pour l'emprunt d'une somme.
– v. Intérêts
composés
– a. Compound interest
Intérieur: qui est dedans.
– ex. un cercle
intérieur à un autre cercle est tel que tous ses points sont confondus avec des
points appartenant au disque de l'autre.
 – v. Extérieur
– v. Extérieur
– a. Interior
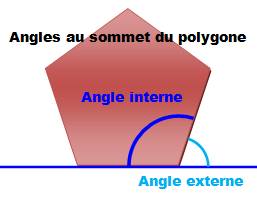
Interne ou intérieur
(angle interne d'un polygone): Angle formé par deux côtés issus du même sommet du polygone.
– a. Interior angle of polygon: inside a polygon, and between two sides of the
polygon
Angle externe ou extérieur: angle formé par un côté du polygone et le côté
voisin prolongé. Angle interne + angle externe = 180°.
– a. Exterior angle of polygon: outside a polygon and between one side and an
extended side.
Interne (loi de
composition -)*: notion qui les opérations comme l'addition ou la multiplication.
Loi binaire: qui associe deux éléments (opérandes)
pour en former un troisième.
Application qui, à deux éléments d'un ensemble E,
associe un élément de E.
– v. Loi de composition, loi de composition externe
– a. Binary operation, dyadic operation
– a. Binary relation, internal law of
composition
The law of composition is a function or application that takes two elements
from two given sets and assigns them to another element, belonging to one of
the two sets.
Interpolation: calcul d'une
variable pour une position intermédiaire à deux valeurs connues ou observées
d'une fonction connue empiriquement.
– v. Prédiction, extrapolation
–
a. Interpolation
Interpolation d'une courbe: fabrication d'une
courbe de tendance à partir d'une fonction classique (linéaire, polynomiale,
exponentielle, logarithmique, spline …) se rapprochant
le plus possible d'une courbe originale.
– a. Polynomial interpolation
Interpolation linéaire: synonyme de selon
une règle de trois ou au prorata; entre deux points donnés, tous les autres
sont donnés par leurs coordonnées sur la droite joignant ces deux points.
– v. Extrapoler
–
a. Linear interpolation
Interpolation graphique: appliquée aux
équations, méthode de représentation géométrique permettant de lire les
solutions sur le tracé.
Intersection:
en
géométrie, synonyme de point de concours ou point de jonction.
– v. Concourantes, sécantes
– a. Point of intersection: we call the place where two lines or curves meet
their point of intersection.
Intersection: en algèbre, ce
sont les éléments communs à deux ensembles.
– notation: ![]() .
.
–
ex. intersection ({a, b}, {b, c)}) = {b}
– v. Intersection,
algèbre de
Boole, opérateur
ET
– a. Intersection, conjonction.
Intersection en probabilité: la formule des probabilités
composées permet de calculer la probabilité d’une intersection d’évènements
(non nécessairement indépendants) à l’aide de probabilités conditionnelles.
– v Vocabulaire des probabilités
Intervalle: ensemble des nombres compris entre deux bornes a et b.
On note l'intervalle entre crochets: [3,1415; 3,1416
]
La longueur de l'intervalle est nommé: amplitude ou
ordre de grandeur de l'encadrement.
– v Intervalle et droite des réels, égal, inférieur, différent,
supérieur, inégalité
– a. Interval, a range of numbers, all the numbers between two given numbers.
Intervalle de confiance: fourchette autour de la valeur moyenne d'un échantillon tel que la moyenne
de la population complète s'y trouve avec une certaine probabilité
(niveau de confiance)
– v Interval de confiance
– a. Interval estimation
Intuitionnisme: philosophie des
mathématiques qui met en avant l'intuition avant le raisonnement. Un objet
n'existe que si on sait le construire au moyen de règles (algorithmes). Par exemple,
l'intuitionnisme n'accepte pas le raisonnement par l'absurde
ou le tiers exclu comme des
principes.
– a. Intuitionism: mathematics is considered to be purely the result of the
constructive mental activity of humans
Mathématiques intuitionnistes: refus de l'infini; pas de tiers exclu
(une proposition est vraie, fausse ou indéterminée); et, une part acceptée
d'aléatoire.
À la place des nombres réels qui contiennent un nombre
infini de décimales, les
mathématiques intuitionnistes représentent ces nombres comme un processus
aléatoire qui se déroule au cours du temps, une décimale après l'autre, de
sorte qu'à chaque instant, il n'existe qu'un nombre fini de décimales, et donc
une quantité finie d'informations.
Invariant:
ce
qui reste constant, qui ne change pas.
L'image est identique à l'antécédent dans
une transformation
ou une suite de transformations.
– ex. le carré
est invariant pour huit opérations de symétrie.
L'ensemble des nombres
pairs est invariant par la multiplication par 2. Ce n'est pas le cas des
impairs.
– v. Invariant
– a. Invariant
Le nombre 2 est un invariant
pour les polyèdres convexes.
Dans tous les cas: sommets + faces – arêtes = 2.
Invariant (point -): un point qui se
transforme en lui-même.
Le transformé de M est confondu avec le point M; T(M) = M.
– a. Invariant points are points on a line or shape which do not move when a
specific transformation is applied.
Invariante (figure -): une figure F est
invariante par une transformation
si tout point de F a pour image un point de F; la figure coïncide avec sa transformée; T(F)
= F
ex: un carré
est une figure invariant par une rotation
de 90° ou 180° ou 270° ou 360° autour de son centre; tout polygone régulier de
n côtés est invariant par une rotation de 360°/n autour de son centre.
– v. Semblable,
homothétique
– a. scale-invariant feature
transform (SIFT): détection de
caractéristiques locales dans l'image utilisée pour la reconnaissance de formes
Invariance d'échelle: propriété vraie à
toutes les échelles.
– Syn. Autosimilarité
(se
reporter à cette entrée)
– v. Fractale
– a. Self-similarity, scale invariance
Invariants topologiques ou propriétés
topologiques*: propriété qui est conservée par l'objet topologique.
– v. Topologie
– a. Invariant (topology)
Invariant relativiste: propriété de
la lumière: sa vitesse est la même dans tout référentiel
galiléen. Invariant
de Lorentz
Inverse: un nombre est l'inverse d'un autre si leur produit
est égal à l'unité.
– ex. 1/3 = 0,333… est l'inverse de 3 (car 3 x 1/3 = 1).
L'inverse de a/b est b/a, car le produit de ces deux fractions donne bien 1.
– notation: 1/x ou x-1.
Tous les nombres ont un inverse sauf le nombre 0, car 1/ 0 n'est pas
défini.
– v. Nombres opposés (à ne pas confondre), élément inverse
– a. Multiplicative inverse or reciprocal
Note: la réciproque d'un théorème se dit converse of a theorem
Inverse modulaire* d'un entier relatif
a pour la multiplication modulo n est un entier u
satisfaisant l'équation : ![]()
–
a. Modular multiplicative inverse
Inverse (fonction – ou opération -) ou opération réciproque: la fonction inverse
est la fonction qui à tout réel x non nul associe son inverse, noté 1/x.
–
synonyme de réciproque.
– a. Multiplicative inverse or reciprocal
Inversible**: Généralisation de
la notion d'inverse aux ensembles
dits monoïdes.
C'est-à-dire à d'autres objets que les nombres et à d'autre opérations que la
multiplication.
Le principe est le même: si y est l'inverse de x, alors x ⊚ y = 1 et y est noté x-1.
Notion de symétrie par rapport à une opération multiplicative.
Le "1" reste l'élément neutre de la multiplication.
– v. Neutre (élément -), vocabulaire
des structures algébriques
– a. Multiplicative inverse or reciprocal, 1 is the multiplicative identity
Inversés (cours ou
classes -): façon d'enseigner en
prenant connaissance soi-même du cours sur une vidéo. Ensuite, le temps de
présence physique du professeur est mis à profit pour déjouer les difficultés
et s'exercer.
– a. flipped classroom
 Inversion: transformation qui inverse les distances par
rapport à un point donné, appelé centre de l'inversion.
Inversion: transformation qui inverse les distances par
rapport à un point donné, appelé centre de l'inversion.
L'image d'un point est d'autant plus éloignée du centre de l'inversion que le
point d'origine en est proche.
Avec le cercle, une droite devient une courbe (Illustration)
Transformation
de centre O et de puissance k, telle qu'un point M' est associé à un point M
avec ![]() ; alors
; alors ![]() .
.
– v. Inversion, inversion avec
le cercle
– a. Inversion transformation
Involution* application
telle que, appliquée deux fois, elle redonne les éléments de départ. Elles sont
telles que f = f-1.
Application bijective qui est sa propre réciproque, c'est-à-dire par laquelle
chaque élément est l'image de son image.
Les symétries
sont involutives.
L'inversion est une involution.
Toute involution est une bijection
– v. vocabulaire
des structures algébriques
– a. Involution, self-inverse function
Irrationnel (nombre -) ou nombre fractionnaire: nombre qui ne peut pas s'exprimer par une fraction (par un ratio).
C'est un nombre de ![]() n'appartenant pas à
n'appartenant pas à ![]() , comme
, comme ![]() .
.
– v. Nombres
rationnels, nombres
algébriques
–
a. Rational number
Irréductible (fraction
-): qui ne peut se simplifier davantage.
Numérateur
et dénominateur sont premiers entre eux.
– a. An irreducible fraction or fraction in lowest terms or reduced fraction.
Isabelle: assistant générique de preuve ou démonstrateur interactif de théorèmes (a higher order logic – HOL). Les formules mathématiques sont exprimées en langage formel et elles sont traitées par des outils d'analyse logique. Développé et réalisé par Larry Paulson à l'université de Cambridge et à l'université technique de Munich.
 ISC: Inverse symbolic
calculator. Outils mathématiques destinés à reconnaitre la nature d'un nombre
réel.
ISC: Inverse symbolic
calculator. Outils mathématiques destinés à reconnaitre la nature d'un nombre
réel.
Exemple: 3,1462…?
c'est ![]() 2 +
2 + ![]() 3.
3.
Le dictionnaire
des nombres: permet d'accéder à ces  nombres par ordre
numérique.
nombres par ordre
numérique.
Le logiciel Maple exécute
cette recherche avec l'instruction identify.
Isoangle
(triangle -): qui possède deux angles égaux.
Désigne aussi bien les triangles
isocèles que les triangles
équilatéraux.
– v. Équiangle
– a. Equiangular
Isobarycentre: barycentre
avec pondération unique. Les coefficients de pondération sont égaux.
Généralisation de la notion de centre
de gravité d'un triangle.
L'isobarycentre G de trois points (A, B, C) est l'unique point tel que ![]() .
.
Isobarycentre et centre
de gravité d'un triangle
homogène sont confondus.
– v. Isobarycentre
Isocèle (triangle -): triangle dont deux
côtés sont égaux.
– étym. Du grec: isos
égal et skelos jambe.
– v. Triangle isocèle, triangle équilatéral
– a. An isosceles triangle has two sides that are the same length and two equal
angles.
Isoèdre: Un
polyèdre isoèdre est un polyèdre convexe dont toutes les faces sont égales.
Il en existe 30.
– a.
Isohedron, isohedral figure
Isogonale (ligne -)*: droite symétrique
par rapport à la bissectrice d'un angle.
– étym. iso gone: qui a des angles
égaux.
– v. Isogonale, symédiane
Isogonale (polygone): tous les angles
sont égaux.
– syn. Équiangle
Isogonale (figure -)*: tous les sommest de la figure sont identiques
(polygones, polyèdres, polytopes). Chaque sommet est entouré du même type de
faces, dans le même ordre et avec les mêmes angles entre faces correspondantes.
Tous les polygones réguliers, qu'ils soient convexes ou étoilés, sont
isogonaux.
– Autre notion liée aux symétries: isotoxal
– a. Isogonal figure
Isogonique (centre -)
ou conjugué isogonal*: point de concours de droites
isogonales. Si dans un triangle les trois droites issues des sommets sont
concourantes, leur conjuguées isogonales sont concourantes en un point dit
conjugué isogonal. Anglais: isogonal
conjugate.
– v. Point de Fermat
– v. Liste
de paires
conjuguées sur le site MathWorld.
Isométrie: transformation
d'une figure dans le plan conservant les distances, les
mesures.
La figure image est "égale" à la figure source.
Translations,
rotations
et symétries
sont des isométries.
– étym. Du grec: égale mesure, de même mesure
– contr. Hétérométrique
– v. Isométrie, congruence,
déplacement, similitude,
transformations du triangle
– a. Isometry or congruence:
distance-preserving transformation
Isométrique: terme plus mathématique
pour dire "égal", "de même forme et de même taille".
– langage: On ne dit plus que deux côtés sont égaux, mais les deux côtés sont isométriques, ou
encore, les deux côtés ont même longueur.
– ex. Triangles isométriques
– v. Égalité
et isométrie
Isomorphe: en gros qui revient
au même, qui a la même forme.
Qui est identique en structure.
Qui est égal modulo une bijection respectant les structures.
 – ex. Tous les rectangles magiques
"semblables" obtenus par permutation des mêmes nombres sont
isomorphes.
– ex. Tous les rectangles magiques
"semblables" obtenus par permutation des mêmes nombres sont
isomorphes.
– ex. L'ensemble des nombres et l'ensemble de leurs logarithmes sont
isomorphes.
– v. Graphes isomorphes, graphes
simples, vocabulaire des structures
algébriques
– a. Isomorphic
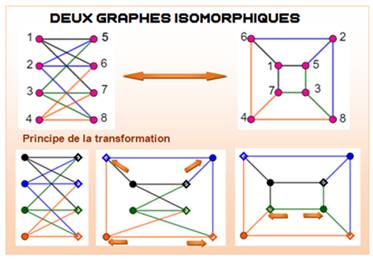
Isomorphique (figures -; graphe -): figures qui se
ressemblent, qui ont la même structure.
Graphes identiques par rotation, symétrie ou déplacement des sommets sans
modifier leurs connexions.
– v. Graphes simples
– a. Isomorphic graph, graph isomorphism
Isomorphisme* homomorphisme bijectif du premier ensemble dans le second.
– v. Morphismes
(types)
– a. Isomorphism: a structure-preserving mapping between two structures of the
same type that can be reversed by an inverse mapping
Isopérimètre: figures qui ont le
même périmètre.
De toutes les figures de périmètre donné, c'est le cercle qui recouvre l'aire
la plus grande.
– v. Isopérimètre
– a. Isoperimeter: Among all planar shapes with the same perimeter the circle
has the largest area.
 Isothétique (polygone): polygone dont les côtés sont inscrits dans le
maillage créé par deux faisceaux de droites concurrentes. (Illustration).
Isothétique (polygone): polygone dont les côtés sont inscrits dans le
maillage créé par deux faisceaux de droites concurrentes. (Illustration).
Les polygones isothétiques sont utilisés en géométrie
algorithmique. Ils sont utilisés pour modéliser les contours des objets.
– étym. du grec: iso,
égal et thetos, position
– a. Isothetic polygon
Un polygone isothétique est un polygone dont
les côtés alternés appartiennent à deux familles paramétriques de droites qui
sont des faisceaux de droites centrées en deux points (éventuellement le point
à l'infini). L'exemple le plus connu de polygones isothétiques sont les
polygones rectilignes, et le premier terme est
couramment utilisé comme synonyme du second.
Isotrope: qui a les mêmes
propriétés dans toutes les directions.
– ex. Une transformation isotrope; les lois de la physiques sont isotropes dans
l'espace.
– a. Isotropy is uniformity in all orientations
Issue: chacune des
éventualités, chacun des cas possibles en probabilité.
– ex. Le dé régulier présente six issues.
– v. Vocabulaire des probabilités,
probabilités
et statistiques
– a. Outcome (et pas issue !)
Itération:
action
de reproduire une opération (un processus), sans fin (mathématique), ou jusqu'à
un critère de fin (informatique).
– ex. "pour i de 1 à 10 calculer et imprimer le carré de i"; i est
appelé le pointeur.
– v. exemples avec la recherche des
chiffres d'un nombre périodique, récursivité
– a. Iteration: repetition of a process in order to generate a sequence of
outcomes.
Itération (sur le résultat): application d'un
procédé en reprenant le résultat obtenu par ce procédé.
– ex. avec le procédé
de Kaprekar
![]()
|
Voir |
|
|
Aussi |
|
|
Autres |
|
|
Cette page |
