|
||||||||||||||||||||||||||||||||||||||||
![]()
|
Nombres de Lychrel PALINDROMES à RETARD ou PALINDROME à RETOURNEMENT Algorithme 196 Palindrome retard: palindrome issu d'Itérations sur un nombre quelconque.
Chaque itération produit la somme du nombre et de son retourné Nombres de Lychrel: nombre sans palindrome retard. Le plus petit est 196. Lychrel = anagramme de Cheryln petite amie de Wade Van Landingham qui a
calculé de nombreux tels nombres (107). Exemple: comment 5 678 devient palindrome en deux itérations
|
Anglais: 196-Algorithm
(Wolfram) / Lychrel number / a reverse-then-add sequence
|
|
|
|
Procédé
Faire la somme des deux. Prendre la somme et son inversée. Les ajouter. Recommencer jusqu'à trouver un Palindrome.
Exemples
Notation
P0 Palindrome naturel. P1
Palindrome obtenu avec une
itération. Pn Palindrome obtenu avec n itérations.
|
|
|
|
||||||
|
N départ |
Opérations |
Ordre |
||||
|
121 |
|
|
|
0 => |
P0 |
|
|
423 |
423 |
+ 324 |
= 747 |
1
=> |
P1 |
|
|
4782 |
4782 7656 14223 |
+ 2874 + 6567 + 32241 |
= 7656 = 14223 = 46464 |
1 2 3
=> |
P3 |
|
|
87 |
87 165 726 1353 |
+ 78 + 561 + 627 + 3531 |
= 165 = 726 = 1353 = 4884 |
1 2 3 4
=> |
P4 |
|
|
1284 |
1284 6105 11121 |
4821 5016 12111 |
= 6105 = 11121 = 23232 |
|
||
|
|
||||
|
|
12 + 21 = 33
Bon 67 + 76 = 143 Mauvais |
|||
|
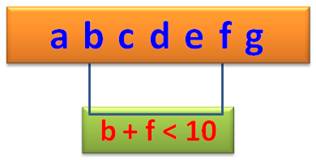
La somme de chaque
couple de chiffres symétriques doit être inférieure à 10. Dans le cas d'une quantité impaire de chiffres,
le chiffre central doit être inférieur à 5. |
|
|||
|
|
Bon 45 + 54 =
99 142 + 241 = 383 1278 + 8721 = 9999 |
Mauvais 19 + 91 =
110 57 + 75 =
132 152 + 251 = 403 149 + 941 = 1 090 1279 + 9721 = 11 000 11522 +
22511 = 34 033 |
||
|
Nécessaire pas suffisante |
Il existe des cas qui donnent un
palindrome du premier coup malgré cette règle. les retenues se compensent ou
se propagent librement du fait de la présence d'un 0. La somme palindromique est
constituée de 0, 1 et 2. |
|||
|
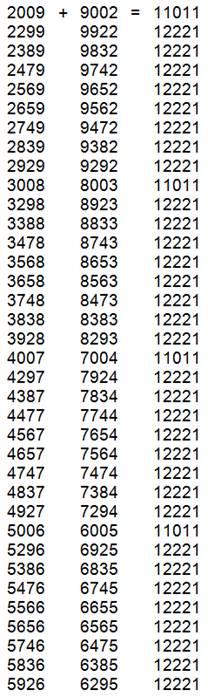
2 et 3 chiffres 29 + 92 = 121 38 + 83 = 121 47 + 74 = 121 56 + 65 = 121 209 + 902 = 1111 308 + 803 = 1111 407 + 704 = 1111 506 + 605 = 1111 |
4 chiffres
|
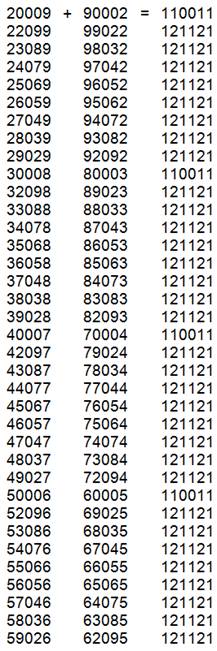
5 chiffres
|
||
|
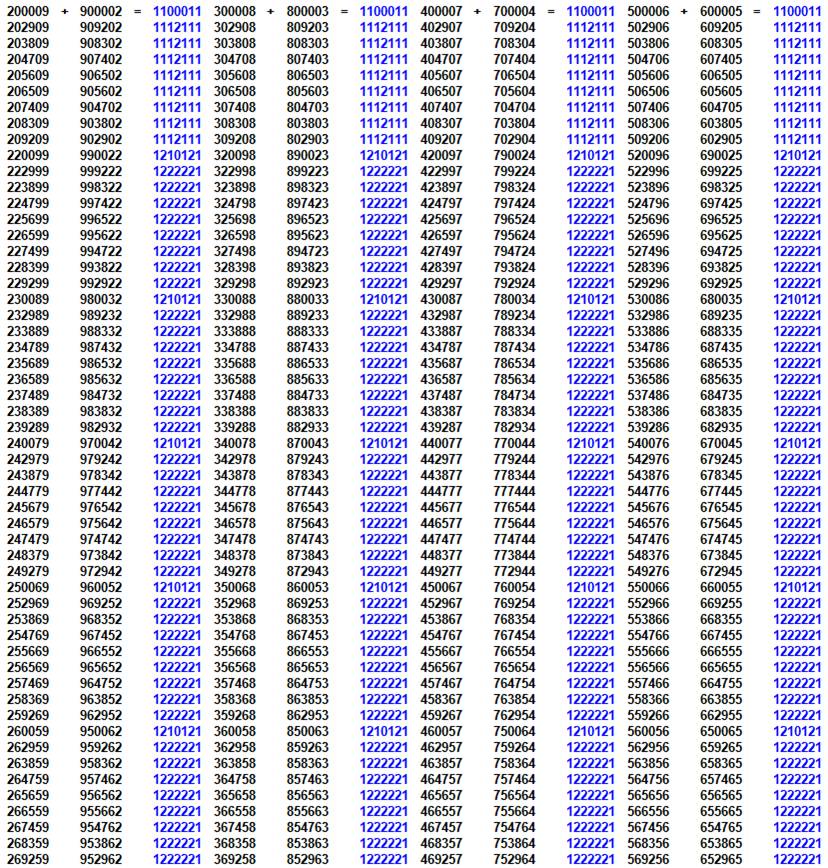
6 chiffres
|
||||
|
|
|
|
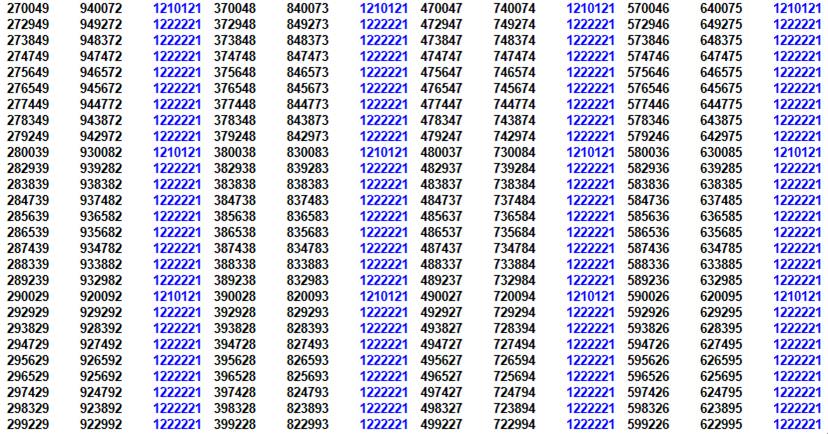
Lecture
Exemples (bleu foncé)
|
|
|
Table
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|||||||||||||||||||||||||||||||||
|
Explication 56 donne
121 en palindrome retard 457 donne 1211
(exception) 4567 donne 12221 =
1231 Etc. |
|||||||||||||||||||||||||||||||||
|
|
|
|
89 187 968 1837 9218 17347 91718 173437 907808 1716517 8872688 17735476 85189247 159487405 664272356 1317544822 3602001953 7193004016 13297007933 47267087164 93445163438 176881317877 955594506548 1801200002107 8813200023188 Palindrome de 13
chiffres obtenu en 25 étapes. Curiosité: 89 est le 24e
nombre premier, soit le 25e en y incluant exceptionnellement le nombre 1. Quant à 13, il apparait curieusement
dans le décompte des nombres premiers. Merci à David H. |
|
|
|
|
|
Exemple: 10110 (22 en décimal) ne donne jamais un
palindrome.
Exemple: 255 en décimal. |
|
|
|
||||||||||||||||||||||||||||||||||
|
||||||||||||||||||||||||||||||||||
Voir Pannumériques
|
|
||||
|
|
Commentaire Ce programme teste un nombre avec le procédé de palindrome retard et
s'arrête dès qu'il trouve un palindrome. Exemple avec 87. L'exploration est limitée à 20 itérations. On imprime le retourné r et le nouveau nombre n. Conversion de n pour disposer d'une liste de chiffres. en N. Indicateur T à 1, supposant que le nombre est palindrome. Test des chiffres symétriques; si différent le nombre n'est pas
palindrome et T = 0. En fin de test, si le nombre n'est pas palindrome on poursuit sinon on
arrête (break). Pour poursuivre, on forme le nombre décimal retourné r et on donne à n
la valeur de la somme de l'ancien n et du retourné r. Résultat en bleu. |
|||
|
Quelque
exemples
|
|
|
||
Voir Programmation – Index / Nombre
196 / Nombre 790
![]()
Plus petit palindrome retard de k itérations
|
Exemple:
Le nombre n = 187 est
le plus petit nombre pour obtenir un palindrome (p) en k = 23 itérations. |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Le
tableau présente les nombres avec k de 30 à 100 qui existent pour n
inférieurs à 100 000.
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Quantité
k d'itérations pour les nombres de 1 à 500 Les nombres avec k = 0
ou k = 1 ne sont pas mentionnés. Il reste 259 nombres. En rouge, nombres de Lychrel (itérations sans fin connue). [19, 2], [28, 2], [37,
2], [39, 2], [46, 2], [48, 2], [49, 2], [57, 2], [58, 2], [59, 3], [64, 2],
[67, 2], [68, 3], [69, 4], [73, 2], [75, 2], [76, 2], [78, 4], [79, 6], [82,
2], [84, 2], [85, 2], [86, 3], [87, 4], [89, 24], [91, 2], [93, 2], [94, 2],
[95, 3], [96, 4], [97, 6], [98, 24], [109, 2], [119, 2], [129, 2], [139, 2],
[149, 2], [150, 2], [152, 2], [153, 2], [154, 2], [155, 3], [156, 3], [157,
3], [158, 3], [159, 2], [160, 2], [162, 2], [163, 2], [164, 3], [165, 3],
[166, 5], [167, 11], [168, 3], [169, 2], [170, 2], [172, 2], [173, 2], [174,
4], [175, 4], [176, 5], [177, 15], [178, 3], [179, 2], [180, 3], [182, 6],
[183, 4], [184, 3], [185, 3], [186, 3], [187, 23], [188, 7], [189, 2], [190,
7], [192, 4], [193, 8], [194, 3], [195, 4], [196, non],
[197, 7], [198, 5], [199, 3], [208, 2], [218, 2], [219, 2], [228, 2], [229,
2], [238, 2], [239, 2], [248, 2], [249, 3], [250, 2], [251, 2], [253, 2],
[254, 3], [255, 3], [256, 3], [257, 3], [258, 2], [259, 2], [260, 2], [261,
2], [263, 3], [264, 3], [265, 5], [266, 11], [267, 3], [268, 2], [269, 2],
[270, 2], [271, 2], [273, 4], [274, 4], [275, 5], [276, 15], [277, 3], [278,
2], [279, 2], [280, 4], [281, 6], [283, 3], [284, 3], [285, 3], [286, 23],
[287, 7], [288, 2], [289, 2], [290, 4], [291, 4], [293, 3], [294, 4], [295, non], [296, 7], [297, 5], [298, 3], [299, 3], [307,
2], [309, 2], [317, 2], [318, 2], [319, 2], [327, 2], [328, 2], [329, 2],
[337, 2], [338, 2], [339, 2], [347, 2], [348, 3], [349, 3], [350, 2], [351,
2], [352, 2], [354, 3], [355, 3], [356, 3], [357, 2], [358, 2], [359, 2],
[360, 2], [361, 2], [362, 3], [364, 5], [365, 11], [366, 3], [367, 2], [368,
2], [369, 2], [370, 2], [371, 2], [372, 4], [374, 5], [375, 15], [376, 3], [377,
2], [378, 2], [379, 2], [380, 6], [381, 4], [382, 3], [384, 3], [385, 23],
[386, 7], [387, 2], [388, 2], [389, 3], [390, 4], [391, 8], [392, 3], [394, non], [395, 7], [396, 5], [397, 3], [398, 3], [399,
3], [406, 2], [408, 2], [409, 2], [416, 2], [417, 2], [418, 2], [419, 2],
[426, 2], [427, 2], [428, 2], [429, 2], [436, 2], [437, 2], [438, 2], [439,
3], [446, 2], [447, 3], [448, 3], [449, 3], [450, 2], [451, 2], [452, 3],
[453, 3], [455, 3], [456, 2], [457, 2], [458, 2], [459, 2], [460, 2], [461,
3], [462, 3], [463, 5], [465, 3], [466, 2], [467, 2], [468, 2], [469, 2],
[470, 2], [471, 4], [472, 4], [473, 5], [475, 3], [476, 2], [477, 2], [478,
2], [479, 2], [480, 4], [481, 3], [482, 3], [483, 3], [485, 7], [486, 2],
[487, 2], [488, 3], [489, 3], [490, 8], [491, 3], [492, 4], [493, non], [495, 5], [496, 3], [497, 3], [498, 3], [499,
3] |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
![]()
|
Suite |
|
|
Voir |
|
|
Aussi |
|
|
DicoNombre |
|
|
Site |
Voir site exhaustif de Patrick De Geest
|
|
Cette page |
![]()