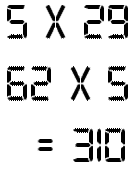|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
![]()
Que lisez-vous ?
Le nombre 2025 et ses retournés 2505, 5052 et 5202
Notez que 2 et 5, avec
ces formes, sont l'un le retourné de l'autre.
|
Nombres retournés ou réversibles Motifs obtenus en prenant un nombre et son retourné ou
symétrique dans un miroir (presque). Objets d'amusements divers. Types de réversibles
Retournés et opérations |
Anglais: Reversal of a positive integer / digit reversal
|
Quel
est l'animal représenté par cette opération:
|
|
Quel
est le nombre de deux chiffres qui présente une
différence de |
|
Quel
est le numéro de la place de parking masqué par la voiture?
|
|
Quelle
est la suite de cette série:
|
Solutions / Somme
30 avec trois nombres
|
Un nombre de deux chiffres ajouté à son
retourné est divisible par
11 et par la somme de ses chiffres. >>> Exemple: 23 + 32 = 55 = 5 x 11.
|
|
|
|||
|
1, 3, 6, 8 et 9 |
|
||
|
11 88 |
Autre: 0, 1, 8, 11, 69, 88, 96, 101,
111 … |
|
|
|
9 89 98 99 696 969 999 … |
|
||
|
69 6 969 … |
Suite
>>> |
||
|
196 = 14² 169 = 13² 961 = 31² |
Suite
>>> |
||
|
11 et 333 |
|
|
121 et 45654 |
|
|
123 et 321 |
|
|
123 et -123 |
|
|
123 et 1/123 |
|
|
11, 69, 88 … |
|
Voir Nombres
et motifs avec les chiffres / Crème renversée
|
122
x 213 = 25 986 221
x 312 = 68 952 |
Relations
|
73 = 37 x 2 – 1 799..993 = 399..997 x 2 – 1 41 = 14 x 3 – 1 |
|
|
||
|
Certains
nombres soustrait de leur retourné produisent des nombres en 9: Propriété assez banale
que l'on retrouve 20 fois pour la centaine en 700: |
Ils sont 17 de n = 10 à 99 avec
somme 9 Ils sont 170 de n = 100 à 999 avec
somme 99 100,
102, 110, 112, 120, 122, 130, 132, 140, 142, 150, 152, 160, 162, 170, 172,
180, 182, 190, 192 … 908, 918, 928, 938, 948, 958, 968, 978, 988, 998 Ils sont 170 de n = 1 000 à 9 999
avec somme 999 1000,
1002, 1110, 1112, 1220, 1222, 1330, 1332, 1440, 1442, 1550, 1552, 1660, 1662,
1770, 1772, 1880, 1882, 1990, 1992… 9008, 9118, 9228, 9338, 9448, 9558, 9668,
9778, 9888, 9998 Ils sont 1700 de n = 10 000 à 99 999
avec somme 9999 10000,
10002, 10100, 10102, 10200, 10202, 10300, 10302, 10400, 10402, 10500, 10502,
10600, 10602, 10700, 10702, 10800, 10802, 10900, 10902, 11010, 11012, 11110,
11112, 11210, 11212, 11310, 11312, 11410, 11412, 11510, … 99098, 99198,
99298, 99398, 99498, 99598, 99698, 99798, 99898, 99998 Le plus grand est toujours de la
forme: 999…98. |
|

Suite Nombres somme
de retournés / Nombre 666
|
|
||
|
Nombres
dont la somme des chiffres est l'un des diviseurs et l'autre diviseur est le
retourné du premier. Seuls
quatre nombres partagent cette propriété (dont un trivial). |
1729 = 19 x 91 & 1 + 7 + 2 + 9 = 19 1458 = 18 x 81 & 1 + 4 + 5 + 8 = 18 81 = 9 x 9 & 8 + 1 = 9 1 = 1 x 1 & 1 = 1 |
|
|
Programme Maple
|
Commentaires Remise à zéro des paramètres internes. Boucle de balayage des nombres de 1 à 100. Le produit donne le nombre p, objet de nos recherches. Il est converti
pour donner la liste des chiffres,
lesquels sont sommés en s. Si cette somme s est égale au nombre n alors nous
avons la configuration cherchée. En bleu,
les quatre cas que nous avons identifiés ci-dessus. La poursuite de
l'examen des nombres (> 100) ne donnent aucun autre résultat. |
|
![]()
|
|
||
|
|
|
|
|
|
||
|
n . r = 100 ab + 10(a² + b²) + ab
n . n = n² = 100 a² + 20 a² + a² = 121 a² 13 x 31 = 100 x 3 + 10 (9 + 1) + 3 = 300 + 100 + 3 = 403 52 x 25 = 100 x 5 x 2 + 10 (5² + 2²) + 5 x 2 = 1 000 + 290
+ 10 = 1 300 99 x 99 = 100 x 81 + 10 x 2 x 81 + 81 = 8 100 + 1 620 + 81
= 9 801 |
||
Voir Calcul
mental / Carré des
repdigits
|
|
||
|
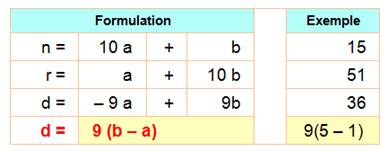
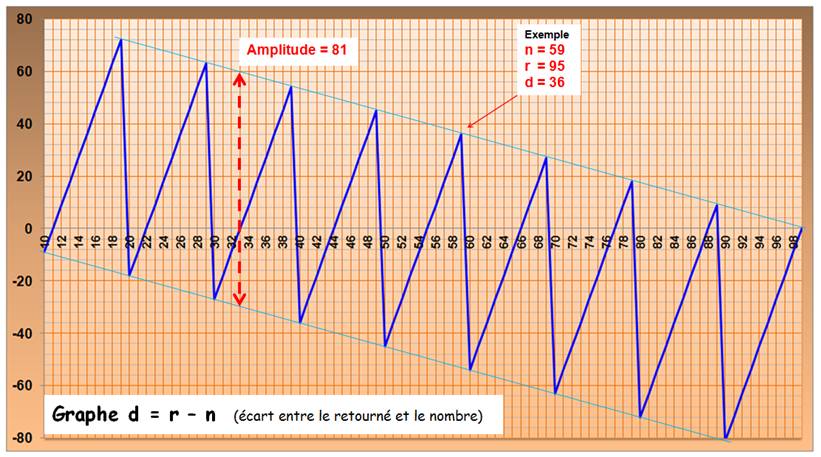
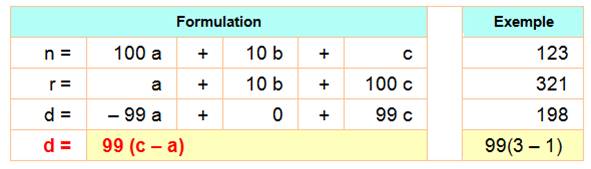
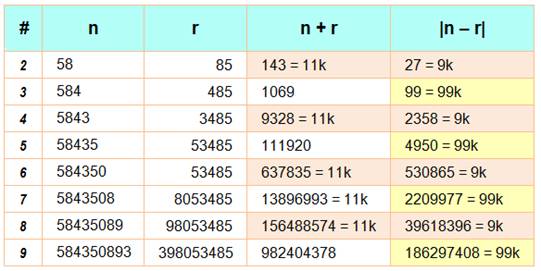
Observations Quantité paire de chiffres n + r divisible par 11 n – r divisible par
9 Quantité impaire de chiffres n – r divisible par
99 Voir Divisibilité |
Exemples avec quantité (#) croissante de chiffres
|
|
|
Démonstration Quantité impaire de chiffres avec pour modèle les nombres à trois chiffres Généralisation à n'importe
quelle quantité impaire de chiffres en donnant le développement
décimal classique de n. |
|
|
|
Quantité paire de chiffres avec pour modèle les nombres à quatre
chiffres Même remarque sur
la généralisation qui me semble évidente,
mais fastidieuse. . |
|
|
|
Pour vous convaincre, prenez seulement deux chiffres de plus:
|
||
Multiples de 9 et de 99
|
Tous les
multiples, de 2 à 10, de 9
ajouté à son retourné donne 99. Tous les
multiples, de 2 à 10, de 99
ajouté à son retourné donne 1 089. Avec 999 x k
=> Avec 9999 x k
=> Etc. |
M = 5 x 9 =
45 Mr = 54 M + Mr = 99 M = 5 x 99 =
495 Mr = 594 M + Mr = 1
089 = 99 + 990 M + Mr = 10
989 = 999 + 9990 M + Mr = 109 989 = 9999 + 99990 … |
Voir
Preuve par neuf / Démonstrations
/ Tour de magie
utilisant ces propriétés / Repdigits
en 9
|
Les sommes complètement retournées
sont nombreuses. Elles sont présentes tant que les sommes n'impliquent aucune
retenue. Avec 12, on trouve ainsi 63 configurations
possibles.
Quantité
de configurations (12, 63; 13,
55; 14, 47; 15, 40; 16,
32; 17, 24; 18, 16; 19,
8) Avec 19, elles sont toutes triviales, du type: 20 + 10 = 30 et 1 + 2 = 3 Avec
trois chiffres, également de nombreuses configurations
Elles sont 447
pour 123 et 25 pour 246, par exemple. Avec
quatre chiffres
Avec
production de retenues
|
Voir Nombres sommes
de nombres et retournés
|
|
||
|
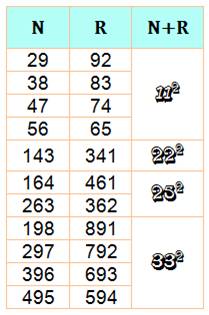
Les
nombres + retournés = carrés
Avec
deux chiffres, ils sont 2 x 4 = 8 avec
11² pour somme. Aucun
à quatre chiffres. Le
premier à cinq chiffres: 10 148 + 84 101 = 307². Avec
plus de chiffres, ils sont de plus en
plus nombreux. |
|
|
|
|
||
|
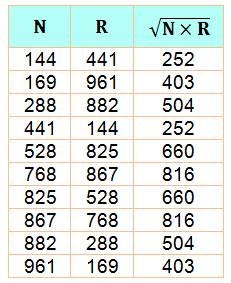
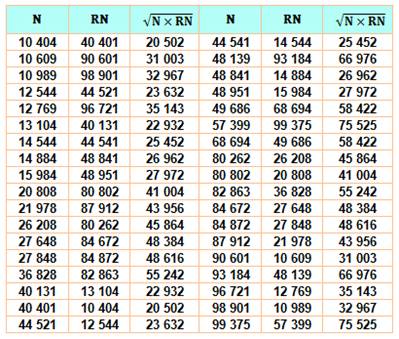
Carré
avec le produit On
élimine les cas évidents
Le
produit d'un nombre de deux chiffres par son retourné n'est jamais un carré
(sauf repdigits. Ex: 33 x 33 = 33²; trivial). Avec
trois chiffres, il y en a cinq
cas, et cinq autres en inversant les
nombres. Avec
quatre chiffres, ils sont 3: 1
089, 1 584 et 2 178 et trois autres
par inversion. Ils
sont 2 x 18 avec cinq chiffres, le
premier étant 10 404 et le dernier 99 375. Ce
triplet est amusant: n = 20 808,
r = 80 802,
nr
= 41 004² Puissances
supérieures Seules
connues: |
|
|
Voir Et avec la division?
Ce sont les palintiples / Brèves
de maths 484
|
|
Commentaires Boucle de recherche pour chaque nombre n. Conversion en base 10 qui produit la liste des
chiffres; quantité de chiffres en q. Calcul du nombre retourné en additionnant les
chiffres à l'envers, et chacun pondéré par la bonne puissance de 10. Calcul du produit en a. Si le nombre n'est pas divisible par 10, si le
nombre n'est pas égal à son retourné et si le produit est un carré (la racine
est entière, integer), alors imprimer le nombre, son retourné, le
produit et la racine carrée. En bleu le résultat de la recherche |
Voir Programmation – Index
|
|
||
|
Comparaison
entre:
En jaune, les cas où il y a égalité, offrant un motif palindrome, comme:
Les repdigits, comme 11 ou 22, produisent un motif trivial. D'autres
cas se produisent, lorsque l'effet de
retenue dans les calculs est absent: 101² =
10201 et 10201 = 101² 102² =
10404 et 40401 = 201² 113² =
12769 et 96721 = 311² etc. Suite
en Nombres carrément réversibles Recherche des carrément réversibles
– Programme |
|
|
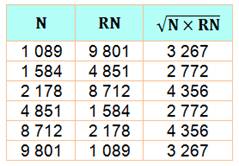
Cas de 33 et 99
|
33²
= 1089 et 9801 = 99² Moins
joli: 3168²
= 10036224 et 42263001 = 6501² |
|
|
||||||||||||||||||||||||||||||||||||
En ajoutant autant de 9 que l'on veut dans
ces nombres, on retrouve la même
propriété. Exemples:
|
||||||||||||||||||||||||||||||||||||
|
954
– 459 = 495 450
– 405 = 45 7641
– 1467 = 6174 98754210
– 1245789 = 97508421 987654321
– 12345678 = 864197532 9876543210
– 12345678 = 975308421 |
|
|
|
|||
|
Nombre
qui s'exprime par deux produits, au
moins, dont l'un est le retourné de
l'autre. Nombre
défini par Shyam Sunder Gupta. |
Le plus petit 2520 = 120 x 021 = 210 x 012 |
||
|
Autres exemples |
4030 = 130 x 031 = 310 x 013, 144648 = 861 x 168 = 492 x 294,
185472 = 672 x 276 = 384 x 483,
9949716 = 2583 x 3852 = 1476 x 6741,
16746912 = 2556 x 6552 = 4473 x 3744. |
||
|
Liste de tels nombres EPRN (Equal
Product of Reversible Numbers) |
2520, 4030, 5740,
7360, 7650, 9760,
10080, 12070, 13000,
14580, 14620, 16120,
17290, 18550, 19440,
22680, 22960, 24300,
25200, 26680, 27010,
29440, 31540, 34780,
36270, 36400, 40300,
40320, 42750, 46060,
49300, 50920, 56050,
57400 … |
||
![]()
|
Quel
est l'animal représenté par cette opération? En retournant
l'opération: (Les nombres sont
écrits en fontes type calculette) En retournant le résultat: |
|
Voir Jeux
avec lettres pour chiffres
|
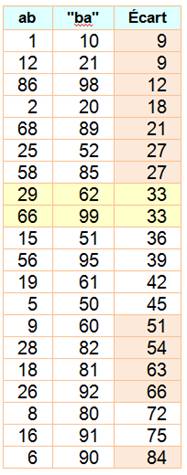
Quel est le nombre de deux chiffres qui présente
une différence de 33 lorsqu'il est lu sur la calculette retournée? Nombres tels qu'en tournant un peu la
tête, on peut lire les deux
possibilités => Deux
réponses possibles: le nombre 29, lu
en retournant la calculette, donne 62
et la différence est 33. C'est le cas aussi pour 66 qui donne 99. Avec
trois chiffres: 699 – 666 =
999 – 966 = 33. Notez aussi: 999 – 669 = 330. Il
faut bien noter que seuls {0, 1, 2,
5, 6, 8 et 9} sont lisibles une fois
retournés, et que 6 devient 9 et
réciproquement. Alors, les différences possibles sont indiquées
dans le tableau (sans compter les cas comme 88 qui devient 88 avec différence
nulle). Le
choix de 33 est amusant, bien que non
lisible à l'envers, mais on aurait pu
choisir tout autre nombre ce cette liste (ceux en rose sont lisibles à
l'envers). |
|
|
Quel est le numéro de
la place de parking masqué par la voiture?
L'astuce: en se
plaçant de l'autre côté, on voit cette
configuration:
Avec cette fonte, les nombres de 86 à 91, sauf 87,
sont réversibles |
|
Suite
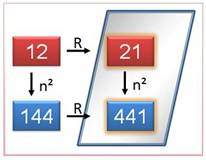
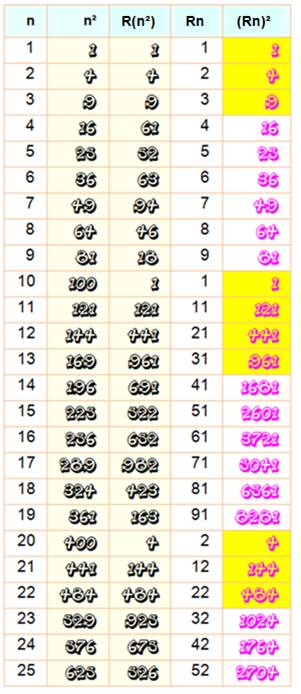
des carrés dont ceux à plusieurs chiffres ont été retournés. 16
est devenu 61; 25 est passé à 52; etc. Pour
10² = 100 le retourné est 001 qui devient simplement 1. La
suite sera 11² = 121 qui restera lui-même. Puis
12² = 144 qui devient 441; et. |
![]()
|
Suite |
|
|
Voir |
|
|
DicoNombre |
|
|
Site |
|
|
Cette
page |
![]()