|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
![]()

Voir Pensées & humour
|
FONCTION
LOGIQUE "IMPLICATION" IMPLICATION INCLUSION Déduction Si A alors B Attention, pas si immédiat à assimiler! La logique s'intéresse à la vérité logique et non
à la vraisemblance du monde réel. |
Anglais : Conditional
|
|
||||
|
Outil
de déduction
|
||||
|
Simple
|
Évolué
|
Particulier
|
||
|
Originale |
Si P alors Q Si c'est un triangle, alors il a
trois côtés. Si l'animal a six pattes, c'est un
insecte. S'il pleut, alors le sol est
mouillé. |
|
|
Réciproque |
Si Q alors P S'il a trois côtés, c'est un
triangle. Si c'est un insecte, l'animal a six
pattes Si le sol est mouillé, c'est qu'il
pleut. |
|
|
Contraposée |
Si non-Q alors non-P S'il n'a pas trois côtés, ce n'est
pas un triangle. S'ils n'a pas six pattes, l'animal
n'est pas un insecte. Si le sol n'est pas mouillé, c'est
qu'il ne pleut pas. |
|
|
La contraposée est la négation des
deux conditions de la réciproque. |
||
|
Équivalente |
Si P alors Q ET si Q alors P Si c'est un triangle, alors il a
trois côtés et réciproquement. Si l'animal a six pattes, c'est un
insecte côtés et réciproquement. MAIS avec s'il pleut, alors le sol
est mouillé la réciproque n'est pas vraie. |
|
|
Seule l'équivalence assure que réciproque et contraposées sont vraies. |
||
|
(Mathématiques
modernes) |
|
|
|
Inclusion
|
||
|
Diagramme de Venn
Voir Diagramme de Venn |
||
|
|
|||||||||||||||||
|
IMPLICATION
|
|||||||||||||||||
|
Table de vérité
Toujours vraie si A est fausse. Même si ça vous paraît étrange! Fonctions S = A => B
|
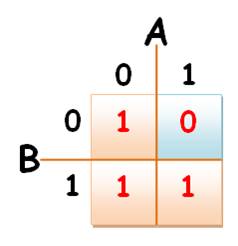
Diagramme de
Karnaugh
|
||||||||||||||||
|
CIRCUITS LOGIQUES / ORDINATEURS |
|
|
|
Circuit
électrique:
À méditer
|
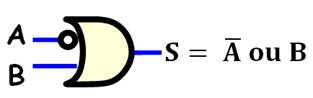
Circuit
électronique:
|
|
|
|
|
|
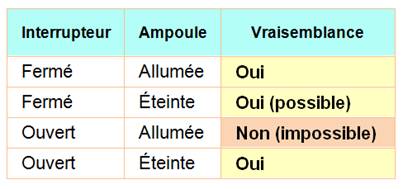
Table de vérité Voici comment il faut interpréter l'illustration
électrique de l'implication
Vous
notez
qu'il
s'agit bien d'une illustration et NON PAS d'un schéma électrique. Ne pas
chercher comme pour le ET ou le OU un résultat sur une sortie électrique. |
|
Bilan
|
Une implication n'est fausse que si A
est vraie et B est fausse. Ainsi,
si A et B sont vraies mais farfelues, l'implication est vraie! Ex: "Le
chien a quatre pattes donc les marguerites ont des pétales" est une
implication vraie. |
![]()
|
Suite |
|
|
Voir |
|
|
Site |
|
|
Cette page |
![]()